Exercise 2.5: "Binomial" or "Poisson"?
From LNTwww
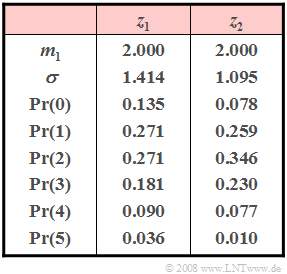
- Betrachtet werden zwei diskrete Zufallsgrößen z1 und z2, die alle ganzzahligen Werte zwischen 0 und 5 (einschließlich dieser Grenzen) annehmen können. Die Wahrscheinlichkeiten dieser Zufallsgrößen sind in nebenstehender Tabelle angegeben. Eine der beiden Zufallsgrößen ist allerdings nicht auf den angegebenen Wertebereich begrenzt.
Weiterhin ist bekannt, dass
- eine der Größen binomialverteilt ist, und
- die andere eine Poissonverteilung beschreibt.
- Nicht bekannt ist, welche der beiden Zufallsgrößen z1 und z2 welcher Verteilung folgt.
- Hinweis: Die Aufgabe bezieht sich auf die Lehrinhalte von Kapitel 2.3 und Kapitel 2.4.
Fragebogen
Musterlösung
- 1. Bei der Poissonverteilung sind Mittelwert m1 und Varianz σ2 gleich. Die Zufallsgröße z1 erfüllt diese Bedingung ⇒ Lösungsvorschlag 1.
- 2. Bei der Poissonverteilung ist der Mittelwert auch gleich der Rate. Deshalb muss λ = 2 gelten.
- 3. Die entsprechende Wahrscheinlichkeit lautet:
- $$\rm Pr(z_1 = 6)=\frac{2^6}{6!}\cdot e^{-2}\hspace{0.15cm} \underline{=0.012}.$$
- Die Wahrscheinlichkeit Pr(z1 > 6) ergibt sich zu 1 – Pr(0) – Pr(1) – ... – Pr(6). Es ergibt sich der Zahlenwert Pr(z1 > 6) ≈ 0.004.
- 4. Für die Varianz der Binomialverteilung gilt:
- $$\sigma^{\rm 2}=\it I\cdot p\cdot (\rm 1-\it p)=\it m_{\rm 1}\cdot (\rm 1-\it p).$$
- Die charakteristische Wahrscheinlichkeit der Binomialverteilung ergibt sich damit aus der Varianz <nobr>1.0952 = 1.2</nobr> und dem Mittelwert 2 entsprechend der Gleichung:
- $$ 1- p = \frac{\sigma^{2}}{m_1}= \frac{1.2}{2} = 0.6\hspace{0.3cm}\Rightarrow \hspace{0.3cm} p \hspace{0.15cm} \underline{= 0.4}.$$
- 5. Aus dem Mittelwert m1 = 2 folgt weiterhin I = 5. Die Wahrscheinlichkeit für den Wert „0” müsste mit diesen Parametern wie folgt lauten:
- $$\rm Pr(z_2 = 0)=\left({5 \atop {0}}\right)\cdot \it p^{\rm 0}\cdot (\rm 1 -\it p)^{\rm 5-0}=\rm 0.6^5=0.078.$$
- Das bedeutet: Das Ergebnis ist richtig.