Exercise 3.6: Noisy DC Signal
From LNTwww
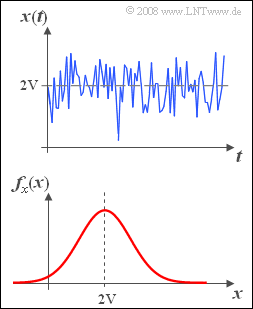
- Ein Gleichsignal s(t) = 2V wird durch ein Rauschsignal n(t) additiv überlagert. Im oberen Bild sehen Sie einen Ausschnitt des Summensignals
- $$x(t)=s(t)+n(t).$$
- Die Wahrscheinlichkeitsdichtefunktion (kurz WDF) des Signals x(t) ist im unteren Bild dargestellt. Die (auf den Widerstand 1 Ω bezogene) Gesamtleistung dieses Signals beträgt Px = 5 V2.
- Verwenden Sie zur Lösung das komplementäre Gaußsche Fehlerintegral Q(x). Nachfolgend finden Sie einige Werte dieser monoton abfallenden Funktion:
- $$\rm Q(0) = 0.5,\hspace{0.9cm} Q(1) = 0.1587,$$
- $$\rm Q(2) = 0.0227, \hspace{0.3cm} Q(3) = 0.0013. $$
- Hinweis: Die Aufgabe bezieht sich auf den gesamten Lehrstoff von Kapitel 3.5.
Fragebogen
Musterlösung
- 1. Das Gleichsignal s(t) ist natürlich nicht gleichverteilt, vielmehr besteht dessen WDF aus nur einer Diracfunktion bei 2 V mit Gewicht 1. Das Signal n(t) ist gaußverteilt und mittelwertfrei. Deshalb ist auch das Summensignal x(t) gaußverteilt, aber nun mit Mittelwert mx = 2 V. Dieser rührt allein vom Gleichsignal s(t) = 2 V her. Richtig sind somit die Lösungsvorschläge 2 und 4.
- 2. Nach dem Satz von Steiner gilt:
- $$\sigma_{x}^{\rm 2}=m_{\rm 2 \it x}-m_{x}^{\rm 2}. $$
- Der quadratische Mittelwert ist gleich der (auf 1 Ω bezogenen) Gesamtleistung Px = 5 V2. Mit dem Mittelwert mx = 2 V folgt daraus für die Streuung: σx = 1 V.
- 3. Die Verteilungsfunktion (VTF) einer gaußverteilten Zufallsgröße mit Mittelwert mx und Streuung σx lautet mit dem Gaußschen Fehlerintegral:
- $$F_x(r)=\rm\phi(\it\frac{r-m_x}{\sigma_x}).$$
- Die Verteilungsfunktion an der Stelle r = 0 V ist gleich der Wahrscheinlichkeit, dass x kleiner oder gleich 0 V ist. Bei kontinuierlichen Zufallsgrößen gilt aber auch Pr(x ≤ r) = Pr(x < r). Mit dem komplementären Gaußschen Fehlerintegral erhält man somit:
- $$\rm Pr(\it x < \rm 0\,V)=\rm \phi(\rm \frac{-2\,V}{1\,V})=\rm Q(\rm 2)\hspace{0.15cm}\underline{=\rm 2.27\%}.$$
- 4. Wegen der Symmetrie um den Wert 2V ergibt sich hierfür die gleiche Wahrscheinlichkeit, nämlich 2.27%.
- 5. Die Wahrscheinlichkeit, dass x(t) größer ist als 3V, ergibt sich zu
- $$\rm Pr(\it x > \rm 3\,V) =\rm 1- \it F_x(\frac{\rm 3\,V-2\,V}{\rm 1V})=\rm Q(\rm 1)=\rm 0.1587.$$
- Für die gesuchte Wahrscheinlichkeit erhält man daraus:
- $$\rm Pr(\rm 3\,V\le \it x \le \rm 4\,V)= \rm Pr(\it x > \rm 3\,V)- \rm Pr(\it x > \rm 4\,V).$$
- Dies liefert den Zahlenwert 0.1587 - 0.0227 = 13.6%.