Exercise 3.10Z: Rayleigh? Or Rice?

• Return to book

Die Wahrscheinlichkeitsdichtefunktion der Zufallsgröße x ist wie folgt gegeben:

$$f_x(x)=\frac{\it x}{\lambda^{2}}\cdot\rm e^{-\it x^{\rm 2}/(\rm 2 \it \lambda^{\rm 2})}.$$

Entsprechend gilt für die zugehörige Verteilungsfunktion:

$$F_x(r)= {\rm Pr}(x \le r) = 1-\rm e^{-\it r^{\rm 2}/(\rm 2 \it \lambda^{\rm 2})}.$$

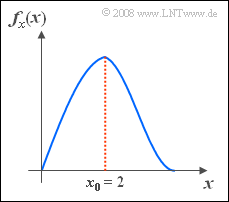
Bekannt ist, dass der Wert x₀ = 2 am häufigsten auftritt. Das bedeutet auch, dass die WDF f_x(x) bei x = x₀ maximal ist.

Hinweis: Diese Aufgabe bezieht sich auf den Lehrstoff von Kapitel 3.7.

Berücksichtigen Sie bei der Lösung das folgende bestimmte Integral:

$$\int_{0}^{\infty}\it x^{\rm 2}\cdot \rm e^{\it -x^{\rm 2}/\rm 2\it} \it \, {\rm d}x=\sqrt{{\pi}/{\rm 2}}.$$

Sie können Ihre Ergebnisse mit nachfolgendem Berechnungstool überprüfen:

WDF, VTF und Momente spezieller Verteilungen

Fragebogen

1

Welche der nachfolgenden Aussagen treffen zu?

	Es handelt sich um eine riceverteilte Zufallsgröße.
	Es handelt sich um eine rayleighverteilte Zufallsgröße.
	Das Zentralmoment 3. Ordnung (μ3) ist 0.
	Die Kurtosis hat den Wert Kx = 3.

2

Welchen Zahlenwert hat hier der Verteilungsparameter λ?

$\lambda$ =

3

Wie groß ist die Wahrscheinlichkeit, dass x kleiner als x₀ ist?

$Pr(x < x_0 )$ =

4

Wie groß ist der Mittelwert der Zufallsgröße x? Interpretation.

$m_x$ =

5

Mit welcher Wahrscheinlichkeit ist x größer als sein Mittelwert m_x?

$Pr (x > m_x)$ =

Musterlösung

Solution

1.  Aufgrund der gegebenen WDF liegt keine Riceverteilung, sondern eine Rayleighverteilung vor. Diese ist um den Mittelwert m_x unsymmetrisch, so dass μ₃ ≠ 0 ist.

Nur bei einer gaußverteilten Zufallsgröße gilt für die Kurtosis K = 3. Bei der Rayleighverteilung ergibt sich aufgrund ausgeprägterer WDF–Ausläufer ein größerer Wert (K = 3.245), und zwar unabhängig von λ. Richtig ist allein der zweite Lösungsvorschlag.

2.  Die Ableitung der WDF nach x liefert:

$$\frac{\rm d\it f_x(x)}{\rm d \it x} = \frac{\rm 1}{\it \lambda^{\rm 2}}\cdot\rm e^{\it -{x^{\rm 2}}/({\rm 2\it \lambda^{\rm 2}})}+\frac{\it x}{\it \lambda^{\rm 2}}\cdot\rm e^{\it -{x^{\rm 2}}/({\rm 2\it \lambda^{\rm 2}})}\cdot(-\frac{\rm 2\it x}{\rm 2\it \lambda^{\rm 2}}).$$

Daraus folgt als Bestimmungsgleichung für x₀ (nur die positive Lösung ist sinnvoll):

$$\frac{\it 1}{\it \lambda^{\rm 2}}\cdot\rm e^{\it -{x_{\rm 0}^{\rm 2}}/{(\rm 2 \it \lambda^{\rm 2}})}\cdot(\rm 1-\frac{\it x_{\rm 0}^{\rm 2}}{\it \lambda^{\rm 2}})=0 \quad \Rightarrow \quad {\it x}_0=\it \lambda.$$

Somit erhält man für den Verteilungsparameter λ = x₀ = 2.

3.  Die gesuchte Wahrscheinlichkeit ist gleich der Verteilungsfunktion an der Stelle r = x₀ = λ:

$$\rm Pr(\it x<x_{\rm 0})=\rm Pr(\it x \le x_{\rm 0})= \it F_x(x_{\rm 0})=\rm 1-\rm e^{-{\it\lambda^{\rm 2}}/({\rm 2\it \lambda^{\rm 2}})}=\rm 1-\rm e^{-0.5}\hspace{0.15cm}\underline{=\rm 0.393}.$$

4.  Der Mittelwert kann beispielsweise nach folgender Gleichung ermittelt werden:

$$m_x=\int_{-\infty}^{+\infty}\hspace{-0.45cm}x\cdot f_x(x)\,{\rm d}x=\int_{\rm 0}^{\infty}\frac{\it x^{\rm 2}}{\it \lambda^{\rm 2}} \cdot \rm e^{-{\it x^{\rm 2}}/({\rm 2\it \lambda^{\rm 2}})}\,{\rm d}\it x = \sqrt{{\rm \pi}/{\rm 2}}\cdot \it \lambda\hspace{0.15cm}\underline{=\rm 2.506}.$$

Der Mittelwert ist natürlich größer als der häufigste Wert x₀ (= Maximalwert der WDF), da die WDF zwar nach unten, aber nicht nach oben begrenzt ist.

5.  Allgemein gilt für die gesuchte Wahrscheinlichkeit:

$$\rm Pr(\it x>m_x)=\rm 1-\it F_x(m_x).$$

Mit der angegebenen Verteilungsfunktion und dem Ergebnis aus (d) erhält man:

$$\rm Pr(\it x>{m_x})=\rm e^{-{\it m_x^{\rm 2}}/({\rm 2\it\lambda^{\rm 2})}}=\rm e^{\rm -\pi/\rm 4}\hspace{0.15cm}\underline{\approx \rm 0.456}.$$