Exercise 4.8Z: AWGN Channel

• Return to book

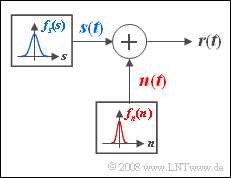
Wir betrachten hier ein analoges Nachrichtensignal s(t), dessen Amplitudenwerte gaußverteilt sind. Der Effektivwert σ_s dieses mittelwertfreien Signals beträgt 1 V. Diese Größe bezeichnet man auch als die Streuung.

Bei der Übertragung wird s(t) von einem Störsignal n(t) additiv überlagert, das ebenso wie s(t) als gaußverteilt und mittelwertfrei angenommen werden kann. Der Effektivwert (die Streuung) des Störsignals sei allgemein σ_n. Es kann angenommen werden, dass zwischen Nutzsignal s(t) und Störsignal n(t) keine statistischen Abhängigkeiten bestehen.

Man bezeichnet eine solche Konstellation als Additive White Gaussian Noise (AWGN) und verwendet als Qualitätskriterium für das Empfangssignal r(t) das Signal-zu-Störverhältnis (Signal-to-Noise-Ratio):

$${\rm SNR} = \frac {\sigma_s^2}{\sigma_n^2}.$$

Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 4.2 und Kapitel 4.3.

Fragebogen

1

Geben Sie die WDF f_r(r) des Empfangssignals r(t) allgemein an. Wie groß ist der Effektivwert σ_r, wenn σ_n = 0.75 V beträgt?

$\sigma_r$ = V

2

Berechnen Sie den Korrelationskoeffizienten, der zwischen den beiden Signalen s(t) und r(t) besteht. Welcher Wert ergibt sich für σ_n = 0.75 V?

$\rho_\text{sr}$ =

3

Berechnen Sie ρ_sr abhängig von SNR. Leiten Sie eine Näherung für große SNR–Werte ab. Welcher Koeffizient ergibt sich für 10 · lg SNR = 30 dB?

$\rho_\text{sr}$ =

Musterlösung

Solution

1.  Es gilt r(t) = s(t) + n(t). Somit kann f_r(r) aus der Faltung der beiden Dichtefunktionen f_s(s) und f_n(n) berechnet werden. Da beide Signale gaußverteilt sind, liefert die Faltung ebenfalls eine Gaußfunktion:

$$f_r(r)= \frac {1}{\sqrt{2 \pi} \cdot \sigma_r} \cdot {\rm e}^{-r^2/(2 \sigma_r^2)}.$$

Die Varianzen von s(t) und n(t) addieren sich. Deshalb erhält man mit σ_s = 1 V und σ_n = 0.75 V:

$$\sigma_r = \sqrt{\sigma_s^2 + \sigma_n^2} =\sqrt{{(\rm 1\hspace{0.1cm}V)^2} + {(\rm 0.75\hspace{0.1cm}V)^2}}\hspace{0.15cm}\underline{ = {\rm 1.25\hspace{0.1cm}V}}.$$

2.  Für den Korrelationskoeffizienten gilt mit dem gemeinsamen Moment m_sr:

$$\rho_{sr } = \frac{m_{sr }}{\sigma_s \cdot \sigma_r}.$$

Hierbei ist berücksichtigt, dass s(t) und auch r(t) mittelwertfrei sind, so dass μ_sr = m_sr gilt. Da s(t) und n(t) als statistisch unabhängig voneinander – und damit unkorreliert – vorausgesetzt wurden, gilt weiter:

$$m_{sr} = {\rm E}[s(t) \cdot r(t)] = {\rm E}[s^2(t)] + {\rm E}[s(t) \cdot n(t)] ={\rm E}[s^2(t)] = \sigma_s^2.$$

Daraus folgt:

$$\rho_{sr } = \frac{\sigma_s}{ \sigma_r} = \sqrt{\frac{\sigma_s^2}{\sigma_s^2 + \sigma_n^2}} = \left (1+ \frac{\sigma_n^2}{\sigma_s^2}\right)^{-1/2}.$$

Mit σ_s = 1 V, σ_n = 0.75 V und σ_r = 1.25 V erhält man ρ_sr = 0.8.

3.  Der in b) berechnete Ausdruck kann mit der Abkürzung SNR = σ_s²/σ_n² wie folgt dargestellt werden:

$$\rho_{sr } = \frac{1}{ \sqrt{1 + \frac{1}{SNR}}} \approx \frac{1}{ {1 + \frac{1}{2 \cdot SNR}}} \approx 1 - \frac{1}{2 \cdot SNR}.$$

Der Signal-zu-Stör-Abstand 10 · lg(SNR) = 30 dB führt zum absoluten Wert SNR = 1000. In die obige Gleichung eingesetzt ergibt dies näherungsweise einen Korrelationskoeffizienten von 0.9995.