Exercise 5.2: Determination of the Frequency Response

• Return to book

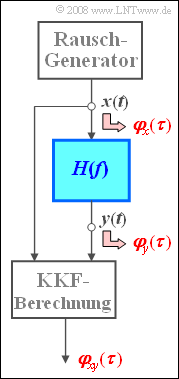
Wir betrachten die abgebildete Messanordnung zur Bestimmung des blau hervorgehobenen Frequenzgangs H(f). Das Eingangssignal x(t) ist weißes Gaußsches Rauschen mit der Rauschleistungsdichte N₀ = 10^–10 W/Hz. Somit gilt für die AKF:

$$\varphi _x ( \tau ) = \frac{N_0 }{2} \cdot \delta ( \tau ).$$

Die gemessene Kreuzkorrelationsfunktion (KKF) zwischen den Signalen x(t) und y(t) kann mit K = 0.628 · 10^–12 W und T₀ = 1 ms wie folgt angenähert werden (nur gültig für positive Zeiten):

$$\varphi _{xy} \left( \tau \right) = K \cdot {\rm{e}}^{ - \tau /T_0 } .$$

Gemessen wird außerdem die AKF φ_y(τ) des Ausgangssignals.

Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 4.6 und Kapitel 5.1. Beachten Sie bitte auch die folgende Fouriertransformation (in ω):

$$H( \omega ) = \frac{1}{{1 + {\rm{j}}\cdot \omega /\omega _0 }}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\,h(t) = \omega _0 \cdot {\rm{e}}^{ - \omega _0 t} \hspace{0.3cm}(t \ge 0).$$

Für negative t-Werte ist dagegen h(t) stets 0.

Fragebogen

1

Welche der folgenden Aussagen treffen zu? Man kann den Frequenzgang H(f) nach Betrag und Phase vollständig bestimmen, wenn:

	die Funktionen φx(τ) und φy(τ) bekannt sind,
	die Funktionen φx(τ) und φxy(τ) bekannt sind,
	die Funktionen φxy(τ) und φy(τ) bekannt sind.

2

Berechnen Sie die Impulsantwort h(t). Welcher Wert ergibt sich für t = T₀?

$h(t = T_0)$ = $\cdot 10^{-3} 1/s$

3

Wie lautet der Frequenzgang H(f)? Welcher Wert ergibt sich für f = 0?

$H(f = 0)$ =

4

Berechnen Sie das Leistungsdichtespektrum des Ausgangssignals y(t). Welcher Wert ergibt sich bei f = 1/(2πT₀)?

$\phi_y(f = 1/(2\pi T_0))$ = $\cdot 10^{-12}\ W/Hz$

Musterlösung

Solution

1.  Bei der AKF-Berechnung gehen Phasenbeziehungen verloren. Die zugehörigen Funktionen Φ_x(f) und Φ_y(f) im Spektralbereich sind rein reell, so dass nur der Betrag |H(f)| angegeben werden kann.

Die Aussagen 2 und 3 sind zutreffend, da folgende Gleichungen gelten:

$$\varphi _{xy} ( \tau ) = h( \tau ) * \varphi _x ( \tau )\quad \Rightarrow \quad H( f ) = \frac{{{\it \Phi} _{xy} ( f )}}{{{\it \Phi} _x ( f )}},$$

$$\varphi _y ( \tau) = \varphi _{xy} ( \tau) * h(- \tau)\quad \Rightarrow \quad H^{\star}( f ) = \frac{{{\it \Phi} _y ( f )}}{{{\it \Phi} _{xy} ( f )}}.$$

2.  Bei diracförmiger Eingangs-AKF φ_x(τ) ist die Impulsantwort h(t) formgleich mit der KKF:

$$h(t) = \frac{{K \cdot {\rm{e}}^{ - t/T_0 } }}{N_0 /2} = 1.256 \cdot 10^{ - 2} \frac{1}{{\rm{s}}} \cdot {\rm{e}}^{ - t/T_0 } .$$

Für t = T₀ ergibt sich der Wert 4.62 · 10^–3 1/s.

3.  Die angegebene Fourierkorrespondenz lautet mit T₀ = 1/ω₀ und C = N₀/2 · T₀/K:

$$h(t) = \frac{C}{T_0 } \cdot {\rm{e}}^{ - t/T_0 }\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, H( \omega ) = \frac{C}{{1 + {\rm{j}}\omega T_0 }}.$$

Die Konstante ergibt sich zu C = 0.08. Mit H(f) = 2π · H(ω) folgt daraus:

$$H(f) = \frac{0.5}{1 + {\rm{j2\pi }}fT_0 }.$$

Damit ergibt sich der Gleichsignalübertragungsfaktor zu 0.5.

4.  Für das Ausgangs-LDS gilt im Allgemeinen bzw. speziell hier:

$${\it \Phi}_y (f) = {\it \Phi} _x (f) \cdot \left| {H(f)} \right|^2 = \frac{N_0 }{2} \cdot \frac{0.5^2 }{{\left( {1 + {\rm{j2\pi }}fT_0 } \right)\left( {1 - {\rm{j2\pi }}fT_0 } \right)}}.$$

Dies führt zum Ergebnis:

$${\it \Phi}_y (f) = {N_0 }/{8} \cdot \frac{1}{1 + \left( {{\rm{2\pi }}fT_0 } \right)^2 }.$$

Bei der angegebenen Frequenz ist Φ_y(f) gegenüber seinem Maximum um die Hälfte abgefallen:

$${\it \Phi}_y (f = 1/(2 \pi T_0)) ={N_0 }/{16}\hspace{0.15cm} \underline{ = 6.25 \cdot 10^{ - 12} \;{\rm{W/Hz}}}.$$