Exercise 3.1: Causality Considerations

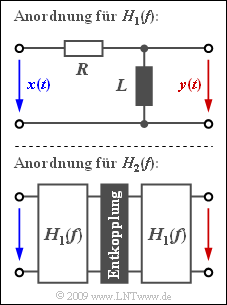
Die Grafik zeigt oben den Vierpol mit der Übertragungsfunktion

$$H_1(f) = \frac{{\rm j}\cdot f/f_{\rm G}}{1+{\rm j}\cdot f/f_{\rm G}} \hspace{0.05cm},$$

wobei f_G die 3dB–Grenzfrequenz angibt:

$$f_{\rm G} = \frac{R}{2 \pi \cdot L} \hspace{0.05cm}.$$

Durch Hintereinanderschalten n gleich aufgebauter Vierpole H₁(f) kommt man zu der Übertragungsfunktion

$$H_n(f) = \left [H_1(f)\right ]^n =\frac{\left [{\rm j}\cdot f/f_{\rm G}\right ]^n}{\left [1+{\rm j}\cdot f/f_{\rm G}\right ]^n} \hspace{0.05cm}.$$

Vorausgesetzt ist hierbei eine geeignete Widerstandsentkopplung, die aber zur Lösung dieser Aufgabe nicht von Bedeutung ist. Die untere Grafik zeigt zum Beispiel die Realisierung der Übertragungsfunktion H₂(f).

In dieser Aufgabe wird ein solcher Vierpol im Hinblick auf seine Kausalitätseigenschaften betrachtet. Bei einem jeden kausalen System erfüllen der Real– und der Imaginärteil der Spektralfunktion H(f) die Hilbert–Transformation, was durch das folgende Kurzzeichen ausgedrückt wird:

$${\rm Im} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad {\rm Re} \left\{ H(f) \right \}\hspace{0.05cm}.$$

Da die Hilbert–Transformation nicht nur für Übertragungsfunktionen, sondern auch für Signale wichtige Aussagen liefert, wird die Korrespondenz häufig durch die allgemeine Variable x ausgedrückt, die je nach Anwendungsfall als normierte Frequenz oder als normierte Zeit zu interpretieren ist.

Hinweis: Die Aufgabe bezieht sich auf das Kapitel 3.1.

Fragebogen

Musterlösung

Solution

1. Mit der angegebenen Übertragungsfunktion kann man nach dem Spannungsteilerprinzip

$$H_1(f = 0) = 0, \hspace{0.2cm}H_1(f \rightarrow \infty) = 1$$

berechnen ⇒ Es handelt sich um einen Hochpass. Für sehr niedrige Frequenzen stellt die Induktivität L einen Kurzschluss dar.

2. Jedes reale Netzwerk ist kausal. Die Impulsantwort h(t) ist gleich dem Ausgangssignal y(t), wenn zum Zeitpunkt t = 0 am Eingang ein extrem kurzfristiger Impuls – ein sog. Diracimpuls – angelegt wird. Aus Kausalitätsgründen kann dann natürlich am Ausgang nicht schon für Zeiten t < 0 ein Signal auftreten:

$$y(t) = h(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} t<0 \hspace{0.05cm}.$$

Formal lässt sich dies folgendermaßen zeigen: Die Hochpass–Übertragungsfunktion H₁(f) kann wie folgt umgeformt werden:

$$H_1(f) = \frac{{\rm j}\cdot f/f_{\rm G}}{1+{\rm j}\cdot f/f_{\rm G}} = 1- \frac{1}{1+{\rm j}\cdot f/f_{\rm G}} \hspace{0.05cm}.$$

Die zweite Übertragungsfunktion beschreibt die zu H₁(f) äquivalente Tiefpassfunktion, die im Zeitbereich zur Exponentialfunktion führt. Die „1” wird zu einer Diracfunktion. Mit T = 2π · f_G gilt somit für t ≥ 0:

$$h_1(t) = \delta(t) - \frac{1}{T} \cdot {\rm e}^{-t/T} \hspace{0.05cm}.$$

Für t < 0 gilt dagegen h₁(t) = 0, womit die Kausalität nachgewiesen wäre ⇒ Antwort Ja.

3. Die Hintereinanderschaltung zweier Hochpässe führt zu folgender Übertragungsfunktion:

$$H_2(f) = \left [H_1(f)\right ]^2 =\frac{\left [{\rm j}\cdot f/f_{\rm G}\right ]^2}{\left [1+{\rm j}\cdot f/f_{\rm G}\right ]^2} =\frac{\left [{\rm j}\cdot f/f_{\rm G}\right ]^2 \cdot \left [(1-{\rm j}\cdot f/f_{\rm G})\right ]^2} {\left [(1+{\rm j}\cdot f/f_{\rm G}) \cdot (1-{\rm j}\cdot f/f_{\rm G})\right ]^2}= \\ = \frac{(f/f_{\rm G})^4 - (f/f_{\rm G})^2 +{\rm j}\cdot 2 \cdot (f/f_{\rm G})^3)} {\left [1+(f/f_{\rm G})^2 \right ]^2}\hspace{0.05cm}.$$

Mit f = f_G folgt daraus:

$$H_2(f = f_{\rm G}) = \frac{1 - 1 +{\rm j}\cdot 2} {4}= \frac{\rm j} {2}$$

$$\Rightarrow \hspace{0.5cm}{\rm Re} \left\{ H_2(f = f_{\rm G}) \right \} = 0, \hspace{0.4cm} {\rm Im} \left\{ H_2(f = f_{\rm G}) \right \} \hspace{0.15cm}\underline{ = 0.5}\hspace{0.05cm}.$$

4. Richtig sind hier die beiden ersten Lösungsvorschläge. Da h₁(t) = 0 für t < 0 ist, erfüllt auch die Faltungsoperation h₂(t) = h₁(t) ∗ h₁(t) die Kausalitätsbedingung. Ebenso ergibt die n–fache Faltung eine kausale Impulsantwort:

$$h_n(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} t<0 \hspace{0.05cm}.$$

Bei kausaler Impulsantwort h₂(t) hängen aber der Real– und der Imaginärteil der Spektralfunktion H₂(f) über die Hilbert–Transformation zusammen. Mit der Abkürzung x = f/f_G und dem Ergebnis aus der Teilaufgabe 3) gilt somit:

$$\frac{x^4- x^2}{x^4+2 x^2+1} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad \frac{2x^3}{x^4+2 x^2+1}\hspace{0.05cm}.$$

	H₁(f) beschreibt einen Tiefpass.
	H₁(f) beschreibt einen Hochpass.

	H₂(f) beschreibt ein kausales System.
	(x⁴–x²)/(x⁴+2x²+1) und 2x³/(x⁴+2x²+1) sind ein Hilbert–Paar.
	Für n > 2 ist die Kausalitätsbedingung nicht erfüllt.

	Ja.
	Nein.