Exercise 4.1: Attenuation Function

Das Dämpfungsmaß α(f) – sprich „alpha” – einer Leitung gibt die auf die Leitungslänge bezogene Dämpfung an. Diese Größe ist durch die Leitungsbeläge R', L', G' und C' festgelegt, wobei die exakte Gleichung etwas kompliziert ist. Daher wurden zwei leichter handhabbare Näherungen entwickelt:

$$\frac{\alpha_{_{\rm I}}(f)}{\rm Np} = \frac{1}{2} \cdot \left [R' \cdot \sqrt{\frac{C'}{ L'} } + G' \cdot \sqrt{\frac{L'}{ C'} }\right ] \hspace{0.05cm},$$

$$\frac{\alpha_{_{\rm II}}(f)}{\rm Np} = \sqrt{\omega \cdot \frac{R' \hspace{0.05cm} C'}{ 2} }\hspace{0.1cm} \bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}\hspace{0.05cm}.$$

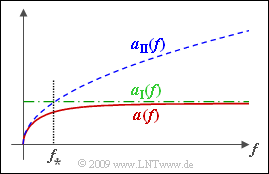
Diese beiden Näherungen sind zusammen mit dem tatsächlichen Verlauf α(f) in der Grafik dargestellt. Der Schnittpunkt von α_I(f) und α_II(f) ergibt die charakteristische Frequenz f_∗ mit folgender Bedeutung:

Für f >> f_∗ gilt α(f) ≈ α_I(f).

Für f << f_∗ ist α(f) ≈ α_II(f).

Mit diesen Näherungen soll das Dämpfungsmaß α(f) für ein Nachrichtensignal der Frequenz f₀ = 2 kHz ermittelt werden, wobei folgende Übertragungsmedien zu betrachten sind:

ein Kupferkabel mit 0.6 mm Durchmesser:

$$R\hspace{0.03cm}' = 130\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} L' = 0.6\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} G\hspace{0.03cm}' = 1\,\,{\rm \mu S}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} C\hspace{0.03cm}' = 35\,\,{\rm nF}/{ {\rm km}} \hspace{0.05cm},$$

eine Bronzefreileitung mit 5 mm Durchmesser:

$$R\hspace{0.03cm}' = 2.2\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} L' = 1.8\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} G\hspace{0.03cm}' = 0.5\,\,{\rm \mu S}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} C\hspace{0.03cm}' = 6.7\,\,{\rm nF}/{ {\rm km}} \hspace{0.05cm}.$$

Die Aufgabe gehört zum Themenkomplex von Kapitel 4.1.

Fragebogen

$Kupfer,\ 0.6\ mm:\ \alpha_I $ =

$Np/km$

$Bronze,\ 5\ mm:\ \alpha_I $ =

$\cdot 10^{-3}\ Np/km$

$Kupfer,\ 0.6\ mm:\ f_∗ $ =

$kHz$

$Bronze,\ 5\ mm:\ f_∗ $ =

$kHz$

$Kupfer,\ 0.6\ mm:\ \alpha (f = f_0) $ =

$Np/km$

$Bronze,\ 5\ mm:\ \alpha (f = f_0) $ =

$\cdot 10^{-3}\ Np/km$

Musterlösung

Solution

1. 2. 3. 4. 5. 6. 7.