Exercise 4.1Z: Transmission Behavior of Short Cables
From LNTwww
- Wir gehen von einer homogenen und reflektionsfrei abgeschlossenen Leitung der Länge l aus, so dass für die Spektralfunktion am Ausgang gilt:
- $$U_2(f) = U_1(f) \cdot {\rm e}^{-\hspace{0.02cm}\gamma(f) \hspace{0.05cm} \cdot \hspace{0.05cm}l} \hspace{0.05cm}.$$
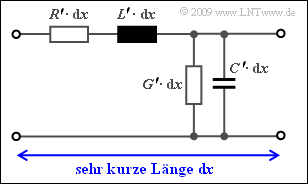
- Hierbei beschreibt γ(f) das Übertragungsmaß einer extrem kurzen Leitung der infinitesimalen Länge dx, das mit den Belägen R', L', G' und C' (siehe Grafik) wie folgt dargestellt werden kann:
- $$\gamma(f) = \sqrt{(R' + {\rm j} \cdot 2\pi f \cdot L') \cdot (G' + {\rm j} \cdot 2\pi f \cdot C')} = \alpha (f) + {\rm j} \cdot \beta (f)\hspace{0.05cm}.$$
- Der Realteil von γ(f) ergibt das Dämpfungsmaß α(f), der Imaginärteil das Phasenmaß β(f). Nach einiger Rechnung kann man für diese Größen schreiben:
- $$\alpha(f) = \sqrt{\frac {1}{2}\cdot \left (R' G' - \omega^2 \cdot L' C'\right)+ \frac {1}{2}\sqrt{(R'^2 + \omega^2 \cdot L'^2) \cdot (G'^2 + \omega^2 \cdot C'^2)}} \hspace{0.1cm}\bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f},$$
- $$\beta(f) = \sqrt{\frac {1}{2}\cdot \left (-R' G' + \omega^2 \cdot L' C'\right)+ \frac {1}{2}\sqrt{(R'^2 + \omega^2 \cdot L'^2) \cdot (G'^2 + \omega^2 \cdot C'^2)}} \hspace{0.1cm}\bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}.$$
- Beim Dämpfungsmaß ist zusätzlich die Pseudoeinheit „Neper (Np)” hinzuzufügen und beim Phasenmaß „Radian (rad)”. Da die Leitungsbeläge jeweils auf die Leitungslänge bezogen sind, weisen α(f) bzw. β(f) die Einheiten „Np/km” bzw. „rad/km” auf.
- Eine weitere wichtige Beschreibungsgröße neben γ(f) ist der Wellenwiderstand ZW(f), der an jedem Ort den Zusammenhang zwischen Spannung und Strom der beiden laufenden Wellen angibt. Es gilt:
- $$Z_{\rm W}(f) = \sqrt{\frac {R' + {\rm j} \cdot \omega L'}{G' + {\rm j} \cdot \omega C'}} \hspace{0.1cm}\bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}.$$
- Hinweis: Die Aufgabe gehört zum Themengebiet von Kapitel 4.1. Verwenden Sie für die numerischen Berechnungen jeweils die Zahlenwerte
- $$R\hspace{0.03cm}' = 100\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} G\hspace{0.03cm}' = 1\,\,{\rm \mu S}/{ {\rm km}}\hspace{0.05cm},\hspace{0.3cm} 2\pi L' = 2\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} 2\pi C\hspace{0.03cm}' = 200\,\,{\rm nF}/{ {\rm km}} \hspace{0.05cm}.$$
Fragebogen
Musterlösung
1.
2.
3.
4.
5.
6.
7.