Exercise 1.7: Entropy of Natural Texts

Anfang der 1950er Jahre schätzte Claude E. Shannon die Entropie H der englischen Sprache mit einem bit pro Zeichen ab. Kurze Zeit später kam Karl Küpfmüller bei einer empirischen Untersuchung der deutschen Sprache auf einen Entropiewert von H = 1.3 bit/Zeichen, also nur etwas größer. Die Ergebnisse von Shannon und Küpfmüller beruhen dabei interessanter Weise auf zwei völlig unterschiedlichen Methoden.

Die differierenden Ergebnisse lassen sich eher nicht mit den geringen Differenzen hinsichtlich des Symbolumfangs M erklären:

Shannon ging von 26 Buchstaben und dem Leerzeichen aus ⇒ M = 27.

Küpfmüller ging von M = 26 Buchstaben aus, ebenfalls ohne zwischen Groß– und Kleinschreibung zu unterscheiden.

Mit dieser Aufgabe soll gezeigt werden, wie sich

Auslöschungen (Erasures) ⇒ man kennt den Ort eines Fehlers,

Zeichenfehler ⇒ es ist nicht offensichtlich, was falsch und was richtig ist,

auf die Verständlichkeit eines Textes auswirken. Unser Text beinhaltet auch die typisch deutschen Buchstaben „ä”, „ö”, „ü” und „ß” sowie Ziffern und Interpunktion. Außerdem wird zwischen Groß– und Kleinschreibung unterschieden.

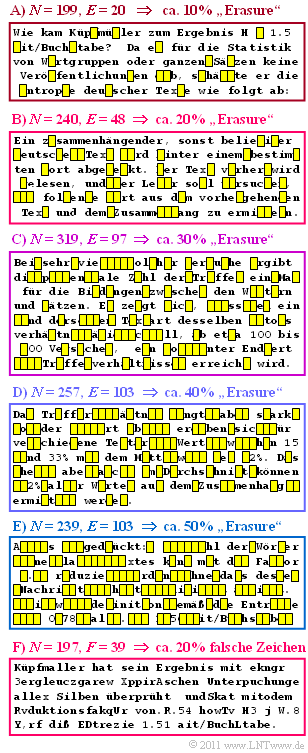
In der Abbildung ist dieser Text, der von Küpfmüllers Vorgehensweise handelt, in sechs Blöcke der Länge N = 197 bis N = 319 aufgeteilt. Beschrieben ist die Überprüfung seiner ersten Analyse (1.3 bit/Zeichen) auf völlig anderem Wege, die zum Ergebnis 1.51 bit/Zeichen führte.

In den oberen fünf Blöcken erkennt man Erasures mit verschiedenen Wahrscheinlichkeiten zwischen 10% und 50%.

Im letzten Block sind Zeichenfehler mit 20–prozentiger Verfälschungswahrscheinlichkeit eingefügt.

Der Einfluss solcher Zeichenfehler auf die Lesbarkeit eines Textes soll in der Teilaufgabe (4) verglichen werden mit dem zweiten (rot umrandeten) Block, für den die Wahrscheinlichkeit eines Erasures ebenfalls 20% beträgt.

Hinweis: Die Aufgabe bezieht sich auf das Kapitel 1.3 dieses Buches. Bezug genommen wird auch auf die relative Redundanz einer Folge, wobei mit dem Entscheidungsgehalt H₀ und der Entropie H gilt:

$$r = \frac{H_0 - H}{H_0}\hspace{0.05cm}.$$

Fragebogen

$M$ =

$r$ =

%

	Eine solche Textdatei hinreichender Länge (N → ∞) könnte man mit 1.3 · N Binärsymbolen darstellen.
	Eine solche Textdatei mit N = 100000 Zeichen könnte man mit 130000 Binärsymbolen darstellen.
	Ein Leser kann den Text auch dann noch verstehen (oder zumindest erahnen), wenn 70% der Zeichen ausgelöscht sind.

	20% Auslöschungen (Erasures),
	eine Zeichenfehlerwahrscheinlichkeit von 20%.

Musterlösung

Solution

1. 2. 3. 4. 5. 6. 7.