Aufgaben:Aufgabe 3.5: Kullback-Leibler-Distanz & Binominalverteilung
Wir gehen hier von der Binomialverteilung aus, die durch die Parameter I und p gekennzeichnet ist ⇒ siehe Buch „Stochastische Signaltheorie”:
- Wertebereich:
- $$X = \{\hspace{0.05cm}0\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}
2\hspace{0.05cm},\hspace{0.05cm} ...\hspace{0.1cm} ,\hspace{0.05cm} {\mu}\hspace{0.05cm}, \hspace{0.05cm}...\hspace{0.1cm} , \hspace{0.05cm} I\hspace{0.05cm}\}\hspace{0.05cm},$$
- Wahrscheinlichkeiten:
- $$P_X (X = \mu) = {I \choose \mu} \cdot p^{\mu} \cdot (1-p)^{I-\mu} \hspace{0.05cm},$$
- linearer Mittelwert:
- $$m_X = I \cdot p \hspace{0.05cm},$$
- Varianz:
- $$\sigma_X^2 = I \cdot p \cdot (1-p)\hspace{0.05cm}.$$
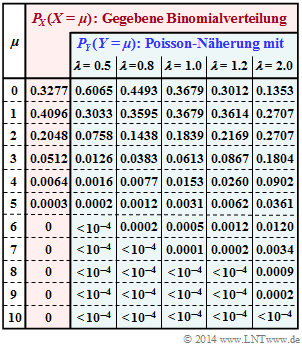
Im rot hinterlegten Teil obiger Tabelle sind die Wahrscheinlichkeiten PX(X = μ) der hier betrachteten Binomialverteilung angegeben. In der Teilaufgabe (a) sollen Sie die dazugehörigen Verteilungsparameter I und p bestimmen.
Diese vorgegebene Binomialverteilung soll hier durch eine Poissonverteilung Y approximiert werden, gekennzeichnet durch die Rate λ:
- Wertebereich:
- $$Y = \{\hspace{0.05cm}0\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}
2\hspace{0.05cm},\hspace{0.05cm} ...\hspace{0.1cm} ,\hspace{0.05cm} {\mu}\hspace{0.05cm}, \hspace{0.05cm}...\hspace{0.1cm}\}\hspace{0.05cm},$$
- Wahrscheinlichkeiten:
- $$P_Y (Y = \mu) = \frac{\lambda^{\mu}}{\mu !} \cdot {\rm e}^{\lambda} \hspace{0.05cm},$$
- Erwartungswerte:
- $$m_Y = \sigma_Y^2 = \lambda\hspace{0.05cm}.$$
Um abschätzen zu können, ob die Wahrscheinlichkeitsfunktion PX(X) ausreichend gut durch PY(Y) approximiert wird, kann man auf die so genannten Kullback–Leibler–Distanzen (KLD) zurückgreifen, teilweise in der Literatur auch relative Entropien genannt. Angepasst an das vorliegende Beispiel lauten diese:
- $$D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y) \hspace{0.15cm} = \hspace{0.15cm} {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_X(X)}{P_Y(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 0}^{I} P_X(\mu) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_X(\mu)}{P_Y(\mu)} \hspace{0.05cm},\\ D(P_Y \hspace{0.05cm}|| \hspace{0.05cm} P_X) \hspace{0.15cm} = \hspace{0.15cm} {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_Y(X)}{P_X(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 0}^{\infty} P_Y(\mu) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_Y(\mu)}{P_X(\mu)} \hspace{0.05cm}.$$
Bei Verwendung des Logarithmus dualis (zur Basis 2) ist hierbei dem Zahlenwert die Pseudo–Einheit „bit” hinzuzufügen.
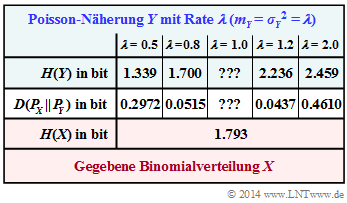
In nebenstehender Ergebnistabelle ist die sog. Kullback–Leibler–Distanz D(PX||PY) in „bit” zwischen der Binomial–PMF PX und einigen Poisson–Näherungen PY (mit fünf verschiedenen Raten λ) eingetragen. Die jeweilige Entropie H(Y), die ebenfalls von der Rate λ abhängt, ist in der ersten Zeile angegeben.
Die Spalten für λ = 1 sind in den Teilaufgaben (3) und (4) zu ergänzen. In der Teilaufgabe (f) sollen diese Ergebnisse interpretriert werden.
Hinweis: Die Aufgabe gehört zu Kapitel 3.1. Um die numerischen Berechnungen in Grenzen zu halten, werden folgende Hilfsgrößen vorgegeben; „lg” bezeichnet den Logarithmus zur Basis 10:
- $$A' \hspace{0.15cm} = \hspace{0.15cm} 0.4096 \cdot {\rm lg} \hspace{0.1cm} \frac{0.4096}{0.3679} + 0.2048 \cdot {\rm lg} \hspace{0.1cm} \frac{0.2048}{0.1839} + 0.0512 \cdot {\rm lg} \hspace{0.1cm} \frac{0.0512}{0.0613} +\\ + \hspace{0.15cm} 0.0064 \cdot {\rm lg} \hspace{0.1cm} \frac{0.0064}{0.0153} + 0.0003 \cdot {\rm lg} \hspace{0.1cm} \frac{0.0003}{0.0031} = \hspace{0.15cm} \underline {= 0.021944} \hspace{0.05cm},$$
- $$B' \hspace{0.15cm} = \hspace{0.15cm} 0.1839 \cdot {\rm lg} \hspace{0.1cm} (0.1839) + 0.0613 \cdot {\rm lg} \hspace{0.1cm} (0.0613) + 0.0153 \cdot {\rm lg} \hspace{0.1cm} (0.0153) +\\ + \hspace{0.15cm} 0.0031 \cdot {\rm lg} \hspace{0.1cm} (0.0031) + 0.0005 \cdot {\rm lg} \hspace{0.1cm} (0.0005) + 0.0001 \cdot {\rm lg} \hspace{0.1cm} (0.0001) \hspace{0.15cm} \underline {= -0.24717} \hspace{0.05cm}.$$
Fragebogen
Musterlösung