Exercise 3.7Z: Rectangular Signal with Echo

• Return to book

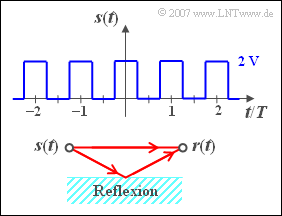
Wir betrachten ein periodisches Rechtecksignal $\text{s(t)}$ mit den möglichen Amplitudenwerten $0 V$ und $2 V$ und der Periodendauer $T_0 = T = 1 \text{ms}$. Bei den Sprungstellen, zum Beispiel bei $t = T/4$, beträgt der Signalwert jeweils $1 V$. Der Gleichanteil (also der Fourierkoeffizient $A_0$) des Signals ist $1 V$.

• Aufgrund der Symmetrie (gerade Funktion) sind alle Sinuskoeffizienten $B_n = 0$.

• Die Koeffizienten $A_n$ mit geradzahligem $n$ sind ebenfalls $0$.

• Für ungeradzahlige Werte von $n$ gilt hingegen:

$$A_n = ( { - 1} )^{\left( {n - 1} \right)/2} \cdot \frac{{4\;{\rm{V}}}}{{n \cdot {\rm{\pi }}}}.$$

Das Signal $\text{s(t)}$ gelangt über zwei Wege zum Empfänger (siehe untere Skizze): Einmal auf dem direkten Pfad und zum zweiten über einen Nebenpfad. Dieser ist durch den Dämpfungsfaktor $\alpha$ und eine Laufzeit $\tau$ gekennzeichnet. Daher gilt für das Empfangssignal:

$$r(t) = s(t) + \alpha \cdot s( {t - \tau } ).$$

Der Frequenzgang des Kanals ist $\text{H(f)} = \text{R(f)}/\text{S(f)}$, die Impulsantwort wird mit $\text{h(t)}$ bezeichnet.

Hinweis: Diese Aufgabe bezieht sich auf den theoretischen Grundlagen von Kapitel 3.4, insbesondere auf die Seite Faltung einer Funktion mit einer Diracfunktion.

Fragebogen

1

Welche Aussagen treffen hinsichtlich der Impulsantwort $\text{h(t)}$ zu?

	Für $0 ≤ t < \tau$ gilt $h(t) = 1$, für $t > \tau$ ist $h(t) = 1 + \alpha$.
	Es gilt $h(t) = \delta (t) + \alpha \cdot \delta(t – \tau)$.
	$h(t)$ verläuft gaußförmig.

2

Berechnen Sie das Signal $\text{r(t)}$ für die Kanalparameter $\alpha = –0.5$ und $\tau = T/4$. Welche Werte ergeben sich bei den normierten Zeiten $t/T = 0.2$ bzw. $0.3$?

$r(t = 0.2 \cdot T)$ = $\text{V}$

$r(t = 0.3 \cdot T)$ = $-$ $\text{V}$

3

Berechnen Sie das Signal $\text{r(t)}$ mit $\alpha = 1$ und $\tau = T/2$. Interpretieren Sie das Ergebnis im Frequenzbereich. Welcher Signalwert ergibt sich bei $t = T/2$?

$r(t = T/2)$ = $\text{V}$

Musterlösung

Solution

1. Die Impulsantwort ist gleich dem Empfangssignal $\text{r(t)}$, wenn am Eingang ein einzelner Diracimpuls zum Zeitpunkt $t = 0$ anliegt:

$$h(t) = \delta (t) + \alpha \cdot \delta( {t - \tau } ).$$

Richtig ist somit der zweite Lösungsvorschlag.

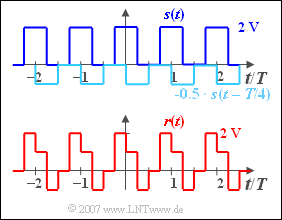
2. Es gilt $\text{r(t)} = \text{s(t)} ∗ \text{h(t)}$. Diese Faltungsoperation lässt sich am einfachsten grafisch ausführen:

Die Werte des Empfangssignals lauten allgemein:

• $0.00 < t/T < 0.25: r(t) = –1 V$,

• $0.25 < t/T < 0.50: r(t) = –1 V$,

• $0.50 < t/T < 0.75: r(t) = 0 V$,

• $0.75 < t/T < 1.00: r(t) = 2 V$.

Die gesuchten Werte sind somit $r(t = 0.2 \cdot T) \underline{= +1 V}$ und $r(t = 0.3 · T) \underline{= –1 V}$.

3. Bei ähnlicher Vorgehensweise wie unter 2) erhält man für $\text{r(t)}$ ein Gleichsignal von $2 V$. Die Lücken im Signal $\text{s(t)}$ werden durch das Echo $\text{s(t – T/2)}$ vollständig aufgefüllt. Dieses Ergebnis lässt sich auch im Frequenzbereich ableiten. Der Kanalfrequenzgang lautet mit $\alpha = 1$ und $\tau = T/2$:

$$H( f ) = 1 + 1 \cdot {\rm{e}}^{ - {\rm{j\pi }}fT} = 1 + \cos ( {{\rm{\pi }}fT} ) - {\rm{j}} \cdot {\rm{sin}}( {{\rm{\pi }}fT} ).$$

Das Eingangssignal $\text{s(t)}$ hat außer dem Gleichanteil nur Anteile bei $f = f_0 = 1/T$, $f = 3 \cdot f_0$, $f = 5 \cdot f_0$ usw.. Bei diesen Frequenzen sind aber sowohl der Real- als auch der Imaginärteil von $\text{H(f)}$ gleich Null. Damit erhält man für das Ausgangsspektrum mit $A_0 = 1 V$ und $H(f = 0) = 2$:

$$R(f) = A_0 \cdot H(f = 0) \cdot \delta (f) = 2\;{\rm{V}} \cdot \delta (f).$$

Die Fourierrücktransformation liefert damit ebenfalls $r(t) \underline{= 2 V = const}$.