System Components of a Baseband Transmission System

Das Kapitel 1 führt in das weite Gebiet der Digitalsignalübertragung ein, wobei einige vereinfachende Annahmen getroffen werden: ein redundanzfreies binäres Sendesignal, keine Impulsinterferenzen. Obwohl die Beschreibung vorwiegend im Basisband erfolgt, lassen sich die Ergebnisse meist auch auf die digitalen Trägerfrequenzsysteme (Kapitel 1.5) übertragen. Im Einzelnen werden behandelt:

der prinzipielle Aufbau und die Komponenten eines Basisbandübertragungssystems,
die Definitionen von Bitfehlerwahrscheinlichkeit und Bitfehlerhäufigkeit (BER),
die Eigenschaften der Nyquistsysteme, die eine impulsinterferenzfreie Übertragung erlauben,
die Optimierung der binären Basisbandsysteme bei Leistungs- und Spitzenwertbegrenzung,
die Verallgemeinerung der Ergebnisse auf Trägerfrequenzsysteme,
die weitgehend gemeinsame Beschreibung von ASK, BPSK und 4–QAM.

Geeignete Literatur:

Benedetto, S.; Biglieri, E.; Castellani, V.: Digital Transmission Theory. Englewood Cliffs, New Jersey: Prentice Hall, 1987.
Hänsler, E.: Statistische Signale: Grundlagen und Anwendungen. 2. Auflage. Berlin – Heidelberg: Springer, 1997.
Hagenauer, J.: Nachrichtentechnik 1. Vorlesungsmanuskript, Lehrstuhl für Nachrichtentechnik, Technische Universität München, 2002.
Hanik, N.: Leitungsgebundene Übertragungstechnik. Vorlesungsmanuskript. Lehrstuhl für Nachrichtentechnik, Technische Universität München, 2008.
Haykin, S.: Digital Communications. New York: John Wiley & Sons, 1988.
Kammeyer, K.D.: Nachrichtenübertragung. Stuttgart: B.G. Teubner, 4. Auflage, 2004.
Lüke, H. D.: Signalübertragung. 8. Auflage. Berlin – Heidelberg: Springer, 2004.
Proakis, J. G.: Digital Communications. 5. Auflage. New York: McGraw-Hill, 2001.
Proakis, J. G.; Salehi, M.: Grundlagen der Kommunikationstechnik. 2. Auflage. München: Pearson Education, 2004.
Söder, G.: Simulationsmethoden in der Nachrichtentechnik. Anleitung zum gleichnamigen Praktikum. Lehrstuhl für Nachrichtentechnik, Technische Universität München, 2000.
Söder, G.; Tröndle, K.: Digitale Übertragungssysteme - Theorie, Optimierung & Dimensionierung der Basisbandsysteme. Berlin – Heidelberg: Springer, 1985.
Tröndle, K.; Söder, G.: Optimization of Digital Transmission Systems. Boston – London: Artech House, 1987.

Vereinfachtes Systemmodell

Im gesamten ersten Kapitel wird für das Digitalsystem von folgendem Blockschaltbild ausgegangen:

Im Vergleich zu einem analogen Übertragungssystem (siehe Buch Modulationsverfahren) erkennt man in diesem vereinfachten Systemmodell folgende Gemeinsamkeiten und Unterschiede:

Das Blockschaltbild ist in beiden Fällen in genau gleicher Weise aufgebaut – bestehend aus Quelle, Sender, Kanal, Empfänger und Sinke – und auch die Signale werden gleich bezeichnet.
Auch beim digitalen Übertragungssystem ist das Empfangssignal $r(t)$ aufgrund der Störungen zeit– und wertkontinuierlich. Das Sendesignal $s(t)$ kann zeit– und wertdiskret sein, muss aber nicht.
Im Unterschied zum Buch Modulationsverfahren sind aber nun das Quellensignal q(t) und das Sinkensignal υ(t) stets Digitalsignale. Sie sind dementsprechend sowohl zeit– als auch wertdiskret.
Alle Informationen über $q(t)$ und $υ(t)$ können somit auch durch die Quellensymbolfolge 〈$q$_ν〉 und die Sinkensymbolfolge 〈$υ$_ν〉 gemeinsam mit der Symboldauer $T$ ausgedrückt werden.
Ein Digitalempfänger unterscheidet sich grundsätzlich vom Empfänger eines Analogsystems, da er zusätzlich eine Entscheidungskomponente zur Gewinnung des digitalen Sinkensignals $υ(t)$ aus dem analogen Empfangssignals $r(t)$ beinhalten muss.
In den ersten drei Kapiteln dieses Buches betrachten wir die digitale Basisbandübertragung, was besagt, dass das Nachrichtensignal $q(t)$ ohne vorherige Frequenzumsetzung (Modulation mit einer Trägerschwingung) übertragen wird.
Deshalb sind hier $s(t)$ und $r(t)$ Tiefpass–Signale und auch für den Kanal (inklusive der Störungen) muss stets von einer Tiefpass–Charakteristik ausgegangen werden.

Nachfolgend werden die Eigenschaften der einzelnen Systemkomponenten detailliert beschrieben, wobei die idealisierenden Voraussetzungen für Kapitel 1 geeignet berücksichtigt werden.

Beschreibungsgrößen der digitalen Quelle

Die digitale Quelle erzeugt die Quellensymbolfolge 〈q_ν〉, die möglichst fehlerfrei zur Sinke übertragen werden soll. Im Allgemeinen entstammt jedes Symbol der zeitlichen Folge 〈q_ν〉 mit ν = 1, 2, ... einem Symbolvorrat {q_μ} mit μ = 1, ... , M, wobei M als Quellensymbolumfang oder auch als Stufenzahl bezeichnet wird. Für das erste Kapitel dieses Buches wird von folgenden Voraussetzungen ausgegangen:

Die Quelle ist binär (M = 2) und die beiden möglichen Symbole sind L („Low”) und H („High”).
Die Quellensymbole sind statistisch unabhängig voneinander, das heißt, die Wahrscheinlichkeit Pr(q_ν = q_μ), dass das ν–te Symbol der Folge 〈q_ν〉 gleich dem μ–ten Symbol des Symbolvorrates {q_μ} ist, hängt nicht von ν ab.
Aufgrund dieser zwei Annahmen wird die digitale Quelle durch die Symbolwahrscheinlichkeiten p_L = Pr(q_ν = L) und p_H = Pr(q_ν = H) = 1– p_L vollständig beschrieben.
Gilt weiterhin p_L = p_H = 0.5, so ist die Quelle redundanzfrei. Meist – jedoch nicht immer – wird im Kapitel 1 eine solche vorausgesetzt.
Der zeitliche Abstand zweier Symbole sei T. Man bezeichnet diese Größe als die Symboldauer und den Kehrwert als die Symbolrate R = 1/T. Bei Binärquellen (M = 2) nennt man diese Größen auch Bitdauer bzw. Bitrate.
Bei systemtheoretischer Betrachtungsweise der digitalen Basisbandübertragung beschreibt man das Quellensignal am besten durch eine Folge gewichteter und verschobener Diracimpulse\[q(t) = \sum_{(\nu)} a_\nu \cdot {\rm \delta} ( t - \nu \cdot T)\hspace{0.05cm}. \]
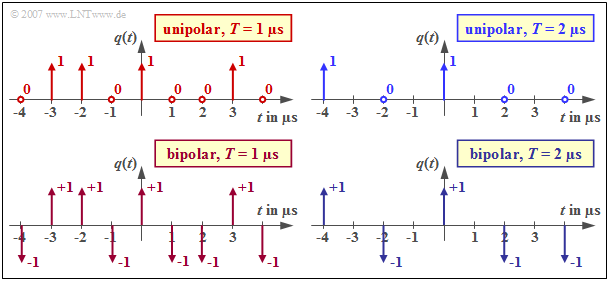
Hierbei bezeichnet man a_ν als die Amplitudenkoeffizienten. Im Falle der binären unipolaren Digitalsignalübertragung gilt:

\[a_\nu = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} q_\nu = \mathbf{H} \hspace{0.05cm}, \\ q_\nu = \mathbf{L} \hspace{0.05cm}. \\ \end{array}\]

Entsprechend gilt bei einem bipolaren (oder antipodischen) System:

\[a_\nu = \left\{ \begin{array}{c} +1 \\ -1 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} q_\nu = \mathbf{H} \hspace{0.05cm}, \\ q_\nu = \mathbf{L} \hspace{0.05cm}. \\ \end{array}\]

Die nachfolgende Beschreibung erfolgt meist für diesen zweiten Fall. Hinweis zur Nomenklatur: In der Literatur wird meist das Symbol H mit 0 bezeichnet. Bei unipolarer Signalisierung wird dann das Symbol 0 durch den Amplitudenkoeffizienten „1” und das Symbol L durch den Zahlenwert „0” dargestellt. Um diesen unschönen Sachverhalt zu vermeiden, wird in LNTwww das Symbol 0 mit H bezeichnet, wobei „High” den Sachverhalt richtig ausdrückt.

Die Grafik zeigt vier binäre diracförmige Quellensignale im Bereich von –4 μs bis +4 μs, wobei jeweils die folgende Quellensymbolfolge zugrundeliegt\[\langle q_\nu \rangle = \langle ... \hspace{0.05cm}, \mathbf{L}, \mathbf{H}, \mathbf{H}, \mathbf{L},\hspace{0.15cm}\mathbf{H}, \hspace{0.15cm}\mathbf{L},\mathbf{L}, \mathbf{H},\mathbf{L},\hspace{0.05cm} ... \rangle \hspace{0.05cm} .\]

Das mittlere, etwas abgesetzte Symbol bezieht sich jeweils auf den Zeitpunkt t = 0.

Die zwei oberen Signale eignen sich zur Beschreibung unipolarer Systeme, die unteren für die bipolare (antipodische) Digitalsignalübertragung. Für die jeweils linken Grafiken ist T = 1 μs vorausgesetzt. Für die beiden rechten gilt dagegen T = 2 μs und damit die halbe Symbolrate.

Kenngrößen des digitalen Senders

Der Sender eines digitalen Übertragungssystems hat die Aufgabe, aus dem (diracförmigen) Quellensignal ein geeignetes Sendesignal s(t) zu erzeugen, das die Nachricht der Quelle vollständig beinhaltet und an die Eigenschaften von Übertragungskanal, Störungen sowie aller technischen Empfangseinrichtungen angepasst ist. Außerdem sorgt der Sender für die Bereitstellung einer hinreichend großen Sendeleistung.

Als Beschreibungsgröße für den Sender verwenden wir den Sendegrundimpuls g_s(t). Aufgrund der Definition des Quellensignals q(t) als Summe von gewichteten und verschobenen Diracfunktionen lässt sich das Sendesignal mit den Amplitudenkoeffizienten a_ν in folgender Weise darstellen: \[s(t) = q(t) \star g_s(t) = \sum_{(\nu)} a_\nu \cdot g_s ( t - \nu \cdot T)\hspace{0.05cm}.\] Häufig wird der Sendegrundimpuls g_s(t) als rechteckförmig mit

der Impulshöhe s₀ = g_s(t = 0) und
der (absoluten) Impulsdauer T_S

angenommen. Gilt T_S < T, so spricht man von einem RZ–Impuls („return–to–zero”), bei T_S = T von einem NRZ–Impuls („non–return–to–zero”).

Bei anderem Sendegrundimpuls, z.B. einem Gauß–, Trapez–, cos²– oder Wurzel–Nyquist–Impuls, verwendet man als Beschreibungsparameter anstelle der absoluten Impulsdauer T_S meist die über das flächengleiche Rechteck definierte äquivalente Impulsdauer : \[\Delta t_{\rm S} = \frac {\int ^{+\infty} _{-\infty} \hspace{0.15cm} g_s(t)\,{\rm d}t}{{\rm Max} \hspace{0.05cm}[g_s(t)]} \le T_{\rm S} \hspace{0.05cm}.\] Nur bei rechteckförmigem Sendegrundimpuls gilt Δt_S = T_S.

Unterscheidet sich die Amplitude des Sendegrundimpulses g_s(t) vom Maximalwert s₀ des Sendesignals s(t), so bezeichnen wir die Impulsamplitude mit A_S. Dies trifft zum Beispiel beim Gaußimpuls zu.

Das folgende Interaktionsmodul zeigt einige geläufige Grundimpulse und die dazugehörigen Spektren :

Impulse und deren Spektren