Exercise 3.2Z: Two-dimensional Probability Mass Function

• Return to book

Wir betrachten die Zufallsgrößen

$X$ = { 0, 1, 2, 3 },

$Y$ = { 0, 1, 2 },

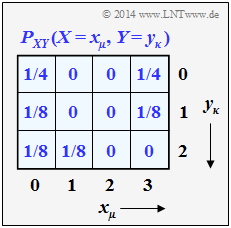
deren gemeinsame Wahrscheinlichkeitsfunktion $P_{X,Y}(X,Y)$ gegeben ist. Aus dieser 2D–Wahrscheinlichkeitsfunktion sollen die eindimensionalen Wahrscheinlichkeitsfunktionen $P_X(X)$ und $P_Y(Y)$ ermittelt werden. Man nennt eine solche manchmal auch Randwahrscheinlichkeit (englisch: Marginal Probability).

Gilt $P_{X,Y}(X,Y)$ = $P_X(X)$ . $P_Y(Y)$, so sind die beiden Zufallsgrößen X und Y statistisch unabhängig. Andernfalls bestehen statistische Bindungen zwischen $X$ und $Y$.

Im zweiten Teil der Aufgabe betrachten wir die Zufallsgrößen

$U$ = { 0, 1 }, $V$ = { 0, 1 },

die sich aus $X$ und $Y$ durch Modulo–2–Operationen ergeben:

$U$ = $X$ mod 2, $V$ = $Y$ mod 2.

Hinweis: Die Aufgabe gehört zum Themengebiet von Kapitel 3.1. Ausgegangen wird hier von der gleichen Konstellation wie in Aufgabe 3.02. Dort wurde die Zufallsgrößen $Y$ = { 0, 1, 2, 3 } betrachtet, allerdings mit dem Zusatz $Pr(Y = 3)$ = 0. Die so erzwungene Eigenschaft $|X| = |Y|$ war in Aufgabe Aufgabe 3.02 zur formalen Berechnung des Erwartungswertes $E[P_X(X)]$ von Vorteil.

Fragebogen

1

Wie lautet die Wahrscheinlichkeitsfunktion $P_X(X)$ ?

$P_X(0)$ =

$P_X(1)$ =

$P_X(2)$ =

$P_X(3)$ =

2

Wie lautet die Wahrscheinlichkeitsfunktion $P_Y(Y)$ ?

$P_Y(0)$ =

$P_Y(1)$ =

$P_Y(2)$ =

3

Sind die Zufallsgrößen $X$ und $Y$ statistisch unabhängig

	Falsch
	Richtig

4

Ermitteln Sie die Wahrscheinlichkeiten $P_{UV}( U, V)$.

$P_{UV}( U = 0, V = 0)$ =

$P_{UV}( U = 0, V = 1)$ =

$P_{UV}( U = 1, V = 0)$ =

$P_{UV}( U =1, V = 1)$ =

5

Sind die Zufallsgrößen $U$ und $V$ statistisch unabhängig

	Falsch
	Richtig

Musterlösung

Solution

1. Man kommt von $P_{XY}(X,Y)$ zur 1D–Wahrscheinlichkeitsfunktion $P_X(X)$ ,indem man alle $Y$-Wahrscheinlichkeiten aufsummiert:

$$P_X(X = x_{\mu}) = \sum_{y \hspace{0.05cm} \in \hspace{0.05cm} Y} \hspace{0.1cm} P_{XY}(x_{\mu}, y)$$

$$\Rightarrow P_X(X = 0) = 1/4+1/8+1/8 = 1/2 = 0.500$$

$$P_X(X = 1)= 0+0+1/8 = 1/8 =0.125$$

$$P_X(X = 2) = 0+0+0 = 0$$

$$P_X(X = 3) = 1/4+1/8+0=3/8 =0.375$$

$$\Rightarrow P_X(X) = [ 1/2, 1/8 , 0 , 3/8 ]$$

2. Analog zur Teilaufgabe (a) gilt nun:

$$P_Y(Y = y_{\kappa}) = \sum_{x \hspace{0.05cm} \in \hspace{0.05cm} X} \hspace{0.1cm} P_{XY}(x, y_{\kappa})$$

$\Rightarrow P_Y(Y= 0) = 1/4+0+0+1/4 = 1/2 = 0.500$

$P_Y(Y = 1) = 1/8+0+0+1/8 = 1/4 = 0.250$

$P_Y(Y = 2) = 1/8+1/8+0+0 = 1/4 = 0.250$

$\Rightarrow P_Y(Y= 0) = [ 1/2, 1/4 , 1/4 ]$

3. Bei Unabhängigkeit sollte $P_{XY}(X,Y)= P_X(X) . P_Y(Y)$ sein.Dies trifft hier nicht zu $\Rightarrow$ Antwort Nein.

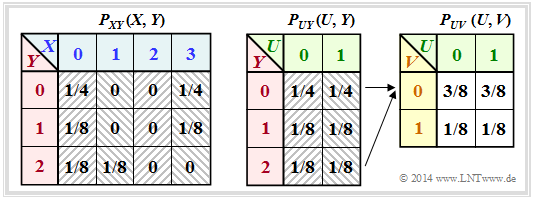
4. Ausgehend von $P_{XY}(X,Y)$ $\Rightarrow$ linke Tabelle kommt man zu $P_{UY}(U,Y)$ $\Rightarrow$ mittlere Tabelle, indem man gewisse Wahrscheinlichkeiten entsprechend $U = X$ zusammenfasst. Berücksichtigt man noch $V = Y mod 2$, so erhält man die gesuchten Wahrscheinlichkeiten entsprechend der rechten Tabelle:

$P_{UV}( U = 0, V = 0) = P_{UV}( U = 0, V = 1) = 3/8 = 0.375$

$P_{UV}( U = 1, V = 0) = P_{UV}( U =1, V = 1) = 1/8 = 0.125$

5.Die 1D–Wahrscheinlichkeitsfunktionen lauten nun:

$P_U(U) = [1/2 , 1/2 ]$, $P_V(V)=[3/4, 1/4]$.

Damit gilt $P_{UV}(U,V) = P_U(U) . P_V(V)$ $\Rightarrow$ $U$ und $V$ sind statistisch unabhängig $\Rightarrow$ Antwort Ja.