Exercise 1.1Z: Binary Entropy Function

• Return to book

Wir betrachten eine Folge von binären Zufallsgrößen mit dem Symbolvorrat {A, B} $\Rightarrow M = 2$. Die Auftrittswahrscheinlichkeiten der beiden Symbole seien $p_A = p$ und $p_B = 1 - p$.

Die einzelnen Folgenelemente sind statistisch unabhängig. Für die Entropie dieser Nachrichtenquelle gilt gleichermaßen:

$$H_{\rm bin}(p) \hspace{0.1cm} = \hspace{0.1cm} p \cdot {\rm ld}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm}} + (1-p) \cdot {\rm ld}\hspace{0.1cm}\frac{1}{1-p}\hspace{0.15cm}{\rm in \hspace{0.15cm} [bit]}\hspace{0.05cm},\\ H'_{\rm bin}(p) \hspace{0.1cm} = \hspace{0.1cm} p \cdot {\rm ln}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm}} + (1-p) \cdot {\rm ln}\hspace{0.1cm}\frac{1}{1-p}\hspace{0.15cm}{\rm in \hspace{0.15cm} [nat]}\hspace{0.05cm}.$$

In diesen Gleichungen werden als Kurzbezeichnungen verwendet:

• der natürliche Logarithmus ln $p = log_e p$,

• der Logarithmus dualis ld $p = log_2 p$.

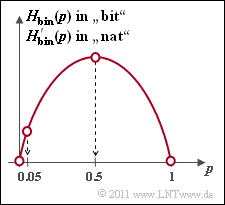
Die Grafik zeigt diese binäre Entropiefunktion in Abhängigkeit des Parameters $p$, wobei $0 ≤ p ≤ 1$ vorausgesetzt wird.

In den Teilaufgaben (5) und (6) soll der relative Fehler ermittelt werden, wenn die Symbolwahrscheinlichkeit $p$ per Simulation (also als relative Häufigkeit $h$) ermittelt wurde und sich dabei fälschlicherweise $h = 0.9 p$ ergeben hat. Der relative Fehler ist dann wie folgt gegeben:

$$\varepsilon_{H} = \frac{H_{\rm bin}(h)- H_{\rm bin}(p)}{H_{\rm bin}(p)}\hspace{0.05cm}.$$

Hinweis: Die Aufgabe gehört zum Kapitel 1.1.

Fragebogen

1

Wie hängen H_bin(p) in bit und H' _bin(p) in nat zusammen?

	Hbin(p) und H' bin(p) unterscheiden sich um einen Faktor.
	Es gilt H' bin(p) = Hbin(ln p).
	Es gilt H' bin(p) = 1 + Hbin(2 p).

2

Zeigen Sie, dass sich das Maximum der binären Entropiefunktion für p = 0.5 ergibt. Wie groß ist H_bin(p = 0.5)?

$H_\text{bin}(p = 0.5)$ = $bit$

3

Berechnen Sie den binären Entropiewert für p = 0.05.

$H_\text{bin}(p = 0.05)$ = $bit$

4

Geben Sie den größeren der beiden p–Werte ein, die sich aus der Gleichung H_bin(p) = 0.5 bit ergeben.

$p$ =

5

Durch unzureichende Simulation wurde p = 0.5 um 10% zu niedrig ermittelt. Wie groß ist der prozentuale Fehler hinsichtlich der Entropie?

$p = 0.45\ statt\ p=0.5:\ \ \epsilon_H$ = - %

6

Durch unzureichende Simulation wurde p = 0.05 um 10% zu niedrig ermittelt. Wie groß ist der prozentuale Fehler hinsichtlich der Entropie?

$p = 0.045\ statt\ p=0.05:\ \ \epsilon_H$ = - %

Musterlösung

Solution

Hinweis: Aus Platzgründen verwenden wir in der Musterlösung „ld” anstelle von „log₂”.

1.  Die Entropiefunktion H' _bin(p) lautet entsprechend der Angabe:

$$H'_{\rm bin}(p) \hspace{0.1cm} = \hspace{0.1cm} p \cdot {\rm ln}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm}} + (1-p) \cdot {\rm ln}\hspace{0.1cm}\frac{1}{1-p} = \\ \hspace{0.1cm} = \hspace{0.1cm} {\rm ln}\hspace{0.1cm}2 \cdot \left [ p \cdot {\rm ld}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm}} + (1-p) \cdot {\rm ld}\hspace{0.1cm}\frac{1}{1-p}\right ]$$

$$\Rightarrow \hspace{0.3cm} H'_{\rm bin}(p) \hspace{0.15cm}{\rm (in \hspace{0.15cm} nat)}= {\rm ln}\hspace{0.1cm}2 \cdot H_{\rm bin}(p) \hspace{0.15cm}{\rm (in \hspace{0.15cm} bit)} = 0.693\cdot H_{\rm bin}(p)\hspace{0.05cm}.$$

Richtig ist also der erste Lösungsvorschlag. Die beiden weiteren Vorgaben machen keinen Sinn.

2.  Die Optimierungsbedingung lautet dH_bin(p)/dp = 0 bzw.

$$\frac{{\rm d}H'_{\rm bin}(p)}{{\rm d}p} \stackrel{!}{=} 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \frac{\rm d}{{\rm d}p} \left [ - p \cdot {\rm ln}\hspace{0.1cm}p - (1-p) \cdot {\rm ln}\hspace{0.1cm}({1-p})\right ] \stackrel{!}{=} 0$$

$$\Rightarrow \hspace{0.3cm} - {\rm ln}\hspace{0.1cm}p - p \cdot \frac {1}{p}+ {\rm ln}\hspace{0.1cm}(1-p) + (1-p)\cdot \frac {1}{1- p}\stackrel{!}{=} 0$$

$$\Rightarrow \hspace{0.3cm} {\rm ln}\hspace{0.1cm}\frac {1-p}{p}= 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\frac {1-p}{p}= 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \underline { p = 0.5}\hspace{0.05cm}.$$

Die Entropiewerte für p = 0.5 lauten somit:

$$H'_{\rm bin}(p = 0.5) \hspace{0.1cm} = \hspace{0.1cm} -2 \cdot 0.5 \cdot {\rm ln}\hspace{0.1cm}0.5 = {\rm ln}\hspace{0.1cm}2 = 0.693 \, {\rm nat}\hspace{0.05cm},\\ H_{\rm bin}(p = 0.5) \hspace{0.1cm} = \hspace{0.1cm} -2 \cdot 0.5 \cdot {\rm ld}\hspace{0.1cm}0.5 = {\rm ld}\hspace{0.1cm}2 \hspace{0.15cm}\underline {= 1 \, {\rm bit}}\hspace{0.05cm}.$$

3.  Für p = 5% erhält man:

$$H_{\rm bin}(p = 0.05) \hspace{0.1cm} = \hspace{0.1cm} 0.05 \cdot {\rm ld}\hspace{0.1cm}\frac{1}{0.05}+ 0.95 \cdot {\rm ld}\hspace{0.1cm}\frac{1}{0.95}= \\ \hspace{0.1cm} = \hspace{0.1cm} \frac{1}{0.693} \cdot \left [ 0.05 \cdot {\rm ln}\hspace{0.1cm}20+ 0.95 \cdot {\rm ln}\hspace{0.1cm}1.053\right ]= \\ \hspace{0.1cm} = \hspace{0.1cm} \frac{1}{0.693} \cdot \left [ 0.05 \cdot 2.995+ 0.95 \cdot 0.051\right ] \hspace{0.15cm}\underline {\approx 0.286 \, {\rm bit}}\hspace{0.05cm}.$$

4.  Diese Aufgabe lässt sich nicht in geschlossener Form lösen, sondern durch „Probieren”. Eine Lösung liefert das Ergebnis:

$$H_{\rm bin}(p = 0.10) = 0.469 \, {\rm bit}\hspace{0.05cm},\hspace{0.2cm}H_{\rm bin}(p = 0.12) = 0.529 \, {\rm bit}\hspace{0.05cm},\hspace{0.2cm} H_{\rm bin}(p = 0.11) \approx 0.5 \, {\rm bit}$$

$$\Rightarrow \hspace{0.3cm}p_1 \approx 0.11\hspace{0.05cm}.$$

Die zweite (gesuchte) Lösung ergibt sich aus der Symmetrie von H_bin(p) zu p₂ = 1 – p₁ = 0.89.

5.  Mit p = 0.45 erhält man H_bin(p) = 0.993 bit. Der relative Fehler bezüglich Entropie ist somit

$$\varepsilon_{H} = \frac{H_{\rm bin}(p = 0.45)- H_{\rm bin}(p= 0.5)}{H_{\rm bin}(p = 0.5)}= \frac{0.993- 1}{1}\hspace{0.15cm}\underline {= -0.7 \, {\rm \%}} \hspace{0.05cm}.$$

Das Minuszeichen deutet darauf hin, dass der Entropiewert H = 0.993 zu klein ist. Hätte die Simulation den zu großen Wert p = 0.55 ergeben, so wäre H und auch der relative Fehler genau so groß.

6.   Es gilt H_bin(p = 0.045) = 0.265 bit. Mit dem Ergebnis aus (3) ⇒ H_bin(p = 0.05) = 0.286 bit folgt daraus für den relativen Fehler bezüglich der Entropie:

$$\varepsilon_{H} = \frac{H_{\rm bin}(p = 0.045)- H_{\rm bin}(p= 0.05)}{H_{\rm bin}(p = 0.05)}= \frac{0.265- 0.286}{0.286}\hspace{0.15cm}\underline {= -7.3 \, {\rm \%}} \hspace{0.05cm}.$$

Eine falsche Bestimmung der Symbolwahrscheinlichkeiten um 10% macht sich für p = 0.05 aufgrund des steileren H_bin(p)–Verlaufs deutlich stärker bemerkbar als für p = 0.5. Eine zu große Wahrscheinlichkeit p = 0.055 hätte zu H_bin(p = 0.055) = 0.307 bit geführt und damit zu einer Verfälschung um ε_H = +7.3%. In diesem Bereich verläuft die Entropiekurve also (mit guter Näherung) linear.