Augenöffnung bei redundanzfreien Mehrstufensystemen (1)
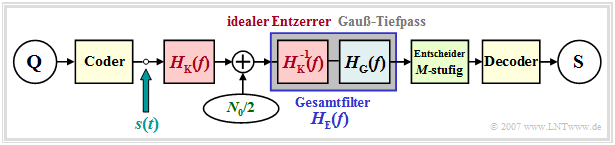
Wir gehen weiterhin von folgenden Voraussetzungen aus:
- NRZ–Rechteck–Sendeimpulse,
- Koaxialkabel und AWGN–Rauschen,
- ideale Kanalentzerrung, sowie
- ein Gaußtiefpass zur Rauschleistungsbegrenzung.
Im Unterschied zu Kapitel 3.3 ist das weiterhin redundanzfreie Sendesignal s(t) nun nicht mehr binär, sondern M–stufig, was sich nur im Wertevorrat der Amplitudenkoeffizienten auswirkt:
\[s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T)\hspace{0.3cm}{\rm mit}\hspace{0.3cm} a_\nu \in \{ a_1, ... , a_\mu , ... , a_{M}\}\hspace{0.05cm}.\]
Dementsprechend besitzt der Entscheider nun nicht mehr nur eine, sondern M – 1 Entscheiderschwellen und im Augendiagramm sind bei geöffnetem Auge M – 1 Augenöffnungen erkennbar.
Vergleicht man die Augendiagramme (ohne Rauschen)
- eines binären (M = 2),
- eines ternären (M = 3), und
- eines quaternären (M = 4)
Übertragungssystems bei gleichem vorgegebenen Detektionsgrundimpuls gd(t) und gleicher Symboldauer T, so erhält man für die halbe vertikale Augenöffnung allgemein:
\[{\ddot{o}(T_{\rm D})}/{ 2} = \frac{g_0}{ M-1} - \sum_{\nu = 1}^{\infty} |g_{-\nu} | - \sum_{\nu = 1}^{\infty} |g_{\nu} |\hspace{0.05cm}.\]
Hierbei bezeichnet g0 = gd(t = 0) wie im Kapitel 3.3 den Hauptwert, während die beiden Summen in obiger Gleichung
- die Vorläufer g1, g2, ... (zweiter Term), und
- die Nachläufer g–1, g–2, ... (dritter Term)
berücksichtigen. Dabei gilt stets gν = gd(t = ν · T).
Auf der nächsten Seite wird diese Gleichung an einem Beispiel verdeutlicht.