Exercise 2.1Z: DSB-AM without/with Carrier

• Return to book

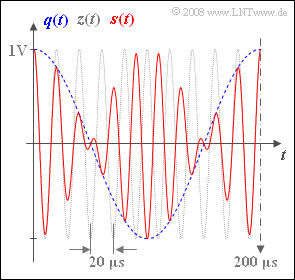
Die Grafik zeigt mit dem roten Kurvenverlauf einen Ausschnitt des Sendesignals$s(t) = q(t) · z(t)$ bei der Zweiseitenband–Amplitudenmodulation (abgekürzt mit ZSB-AM) ohne Träger. Die Dauer des Zeitausschnitts beträgt $200 μs$.

Zusätzlich sind das Quellensignal (als blau–gestrichelte Kurve) $$q(t) = 1\,{\rm V} \cdot \cos(2 \pi f_{\rm N} t + \phi_{\rm N})$$ und das Trägersignal (grau–gepunkteter Verlauf) $$z(t) = 1 \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T})$$ in der nebenstehenden Grafik eingetragen.

Ab der Teilaufgabe d) wird die „ZSB–AM mit Träger” betrachtet. Dann gilt mit $A_T = 2 V$: $$s(t) = \left(q(t) + A_{\rm T} \right) \cdot z(t) \hspace{0.05cm}.$$

Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 2.1.

Fragebogen

1

Ermitteln Sie die Phasenwerte von Quellen– und Trägersignal aus der Grafik.

$\phi_N$ = $\text{Grad}$

$\phi_T$ = $\text{Grad}$

2

Wie lauten die Frequenzen von $q(t)$ und $z(t)$?

$f_N$ = $\text{KHz}$

$f_T$ $\text{KHz}$

3

Analysieren Sie die Nulldurchgänge von $s(t)$. Welche Aussagen treffen zu?

	Alle Nulldurchgänge von $z(t)$ bleiben in $s(t)$ erhalten.
	Es gibt weitere Nullstellen, verursacht durch $q(t)$.
	Es gilt $s(t) = a(t) · cos(ω_T · t)$ mit $a(t) = |q(t)|$.

4

Bestimmen Sie die Spektralfunktion $S(f)$ über die Faltung. Welche (positiven) Frequenzen $f_1$ und $f_2 > f_1$ sind im Signal enthalten?

$f_1$= $\text{KHz}$

$f_2$ = $\text{KHz}$

5

Es gelte nun $A_T = 2 V$. Wie groß ist der Modulationsgrad?

$m$ =

6

Welche der Aussagen treffen bei der „ZSB–AM mit Träger” und $A_T = 2 V$ zu?

	$S(f)$ beinhaltet nun auch Diracfunktionen bei $±f_T$.
	Die Gewichte dieser Diraclinien sind jeweils 2 V.
	$q(t)$ ist in der Hüllkurve von $s(t)$ zu erkennen.
	Durch den zusätzlichen Trägeranteil bleibt die Leistung unverändert.

Musterlösung

Solution

1. 2. 3. 4. 5. 6. 7.