Aufgaben:Aufgabe 2.11Z: Nochmals ESB-AM & Hüllkurvendemodulation

• Return to book

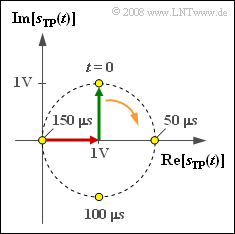
Nebenstehende Grafik zeigt die Ortskurve – also die Darstellung des äquivalenten TP–Signals in der komplexen Ebene – für ein ESB–AM–System.

Weiter ist bekannt, dass die Trägerfrequenz $f_T = 100 kHz$ beträgt und dass der Kanal ideal ist: $$ r(t) = s(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} r_{\rm TP}(t) = s_{\rm TP}(t) \hspace{0.05cm}.$$

Beim Empfänger wird ein idealer Hüllkurvendemodulator (HKD) eingesetzt. Im Verlauf dieser Aufgabe werden folgende Größen benutzt:

• das Seitenband–zu–Träger–Verhältnis

$$\mu = \frac{A_{\rm N}/2}{A_{\rm T}}\hspace{0.05cm},$$

• die Hüllkurve

$$a(t) = |s_{\rm TP}(t)| \hspace{0.05cm},$$

• die maximale Abweichung $τ_{max}$ der Nulldurchgänge von $s(t)$ und Trägersignal $z(t)$.

Hinweis: Die Aufgabe bezieht sich auf den Theorieteil von Kapitel 2.4. Für diese Aufgabe gelten vergleichbare Voraussetzungen wie für die Aufgabe A2.10.

Fragebogen

1

Geben Sie das äquivalente TP–Signal in analytischer Form an und beantworten Sie folgende Fragen.

	Es handelt sich um eine OSB–AM.
	Es handelt sich um eine USB–AM.
	Das Nachrichtensignal $q(t)$ ist cosinusförmig.
	Das Nachrichtensignal $q(t)$ ist sinusförmig.

2

Geben Sie die Amplitude und Frequenz des Quellensignals an. Berücksichtigen Sie, dass es sich um eine ESB–AM handelt.

$A_N$ = $V$

$f_N$ = $KHz$

3

Welcher Wert ergibt sich für das sog. Seitenband–zu–Träger–Verhältnis $μ$? Verwenden Sie diese Größe zur Beschreibung von $s_{TP}(t)$.

$μ$ =

4

Berechnen Sie den zeitlichen Verlauf der Hüllkurve $a(t)$. Welche Werte treten bei $t = 50 μs$, $t = 100 μs$ und $t = 150 μs$ auf?

$a(t = 50 μs)$ = $V$

$a(t = 100 μs)$ = $V$

$a(t = 150 μs)$ = $V$

5

Um welche Zeitdifferenz τmax (betragsmäßig) sind die Nulldurchgänge von $s(t)$ gegenüber $z(t)$ maximal verschoben?

$τ_{max}$ = $μs$

Musterlösung

Solution

1. 2. 3. 4. 5. 6. 7.