Übertragungsfunktion und Impulsantwort
Die Beschreibungsgrößen eines Nachrichtenübertragungssystems wurden bereits in Kapitel 1.1 bzw. Kapitel 1.2 des Buches „Lineare zeitvariante Systeme” eingeführt und eingehend diskutiert. Die wichtigsten Ergebnisse sollen hier nochmals kurz zusammengefasst werden.
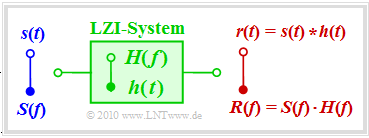
Vorausgesetzt wird zunächst ein lineares und zeitinvariantes System ⇒ LZI–System mit dem Signal s(t) am Eingang und dem Ausgangssignal r(t). Der Einfachheit halber seien s(t) und r(t) reell. Dann gilt:
- Das System lässt sich vollständig durch die Übertragungsfunktion H(f) charakterisieren. Man bezeichnet H(f) auch als den Frequenzgang. Definitionsgemäß gilt H(f) = R(f)/S(f).
- Ebenso ist das System durch die Impulsantwort h(t) als die Fourierrücktransformierte von H(f) vollständig gekennzeichnet. Das Ausgangssignal ergibt sich aus der Faltung:
- \[r(t) = s(t) \star h(t) \hspace{0.4cm} {\rm mit} \hspace{0.4cm} h(t) \hspace{0.2cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.2cm} H(f) \hspace{0.05cm}.\]
Um die durch H(f) bzw. h(t) entstehenden linearen Verzerrungen zu erkennen, eignen sich die folgenden Eingangssignale:
- ein Diracimpuls: s(t) = δ(t) ⇒ r(t) = h(t) ⇒ Impulsantwort,
- eine Sprungfunktion: s(t) = γ(t) ⇒ r(t) = γ(t) ∗ h(t) ⇒ Sprungantwort,
- ein Diracpuls: s(t) = pδ(t) ⇒ r(t) = pδ(t) ∗ h(t) ⇒ Pulsantwort.
Dagegen ist ein Gleichsignal s(t) = A nicht geeignet, die Frequenzabhängigkeit des LZI–Systems sichtbar werden zu lassen. Bei einem Tiefpass–System wäre dann das Ausgangssignal unabhängig von H(f) stets konstant: r(t) = A · H(f = 0).
Auf der nächsten Seite betrachten wir als Eingangssignal s(t) einen Diracpuls pδ(t). Hiermit lassen sich die Gemeinsamkeiten und Unterschiede zwischen zeitinvarianten und zeitvarianten Systemen sehr anschaulich darstellen.
Hinweis: Die Eigenschaften von H(f) und h(t) werden in einem Lernvideo behandelt:
Anmerkungen zur Übertragungsfunktion Please add link and do not upload flash videos (Dauer 9:08)