Exercise 4.10Z: Signal Space Constellation of the 16-QAM

• Return to book

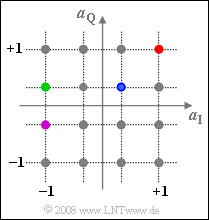
Wir betrachten weiter das 16–QAM–Verfahren entsprechend dem im Theorieteil angegebenen Blockschaltbild. Die Grafik zeigt die möglichen komplexen Amplitudenkoeffizienten $a = a_I + j · a_Q$. Für diese Aufgabe soll ebenso wie für die Aufgabe A4.9 vorausgesetzt werden:

• Die möglichen Amplitudenkoeffizienten $a_I$ und $a_Q$ der beiden Komponentensignale sind jeweils ±1 und ±1/3.
• Der Sendegrundimpuls $g_s(t)$ ist rechteckförmig und weist die Amplitude $g_0 = 1 V$ und die Dauer $T = 1 μs$ auf.
• Das Quellensignal $q(t)$ vor dem Seriell–Parallel–Wandler ist binär und redundanzfrei.

Hinweis: Die Aufgabe gehört zum Themengebiet von Kapitel 4.3. Die zu den farbigen Punkten gehörigen Signale sind auf der Angabenseite zur Aufgabe A4.9 in gleicher Farbe dargestellt.

Fragebogen

1

Wie groß ist die Bitrate des binären Quellensymbols?

$R_B$ = $Mbit/s$

2

Geben Sie den Betrag und die Phase (zwischen ±180°) für das rote Symbol an.

$a = 1 + j: |a|$ =

$arc (a)$ = $Grad$

3

Geben Sie den Betrag und die Phase für das blaue Symbol an.

$ a = 1/3 + j/3: |a|$ =

$arc (a)$ = $Grad$

4

Geben Sie den Betrag und die Phase für das grüne Symbol an.

$ a = –1 + j/3: |a|$ =

$arc (a)$ = $Grad$

5

Geben Sie den Betrag und die Phase für das violette Symbol an.

$ a = –1 – j/3: |a|$ =

$arc (a)$ = $Grad$

6

Wieviele unterschiedliche Beträge ($N_{|a|}$) = und Phasenlagen ($N_{arc}$) sind möglich?

$N_{|a|}$ =

$N_{arc}$ =

Musterlösung

Solution

1. 2. 3. 4. 5. 6. 7.