Exercise 1.2Z: Sets of Digits

• Return to book

Sets of digits:  $A$,  $B$,  $C$

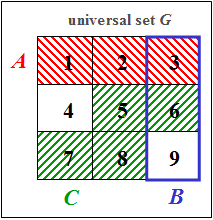
Let the universal set  $G$  be the set of all digits between  $1$  and  $9$.  Given are the following subsets:

$$A = \big[\text{digits} \leqslant 3\big],$$

$$ B = \big[\text{digits divisible by 3}\big],$$

$$ C = \big[\text{digits 5, 6, 7, 8}\big].$$

Besides these,  let other sets be defined:

$$D = (A \cap \overline B) \cup (\overline A \cap B),$$

$$E = (A \cup B) \cap (\overline A \cup \overline B), $$

$$F = (A \cup C) \cap \overline B, $$

$$H = (\overline A \cap \overline C) \cup (A \cap B \cap C).$$

First consider which digits belong to the sets  $D$,  $E$,  $F$  and  $H$  and then answer the following questions.
Justify your answers in terms of set theory.

Hints:

• The task belongs to the chapter  Set Theory Basics.

• The topic of this chapter is illustrated with examples in the  (German language)  learning video

Mengentheoretische Begriffe und Gesetzmäßigkeiten   $\Rightarrow$   "Set Theoretical Concepts and Laws".

Questions

1

Which of the following statements are correct?

	$A$  and  $B$  are disjoint sets.
	$A$  and  $C$  are disjoint sets.
	$B$  and  $C$  are disjoint sets.

2

Which of the following statements are correct?

	The union  $A \cup B \cup C$  gives the universal set  $G$.
	The complementary set to  $A \cap B \cap C$  gives the universal set  $G$.

3

Which of the following statements are correct?

	The complementary sets of  $D$  and  $E$  are identical.
	$F$  is a subset of the complementary set of  $B$.
	The sets  $B$,  $C$  and  $D$  form a complete system.
	The sets  $A$,  $C$  and  $H$  form a complete system.

Solution

Solution

For the other sets defined in the problem holds:

$$ D = (A \cap \overline B) \cup (\overline A \cap B) =\big[\{1, 2, 3\} \cap \{1, 2, 4, 5, 7, 8\}\big] \cup \big[\{4, 5, 6, 7, 8, 9\} \cap \{3, 6, 9\}\big] = \{1, 2, 6, 9\},$$

$$ E = (A \cup B) \cap (\overline A \cup \overline B) = (A \cap \overline A) \cup (A \cap \overline B) \cup (\overline A \cap B) \cup (\overline A \cap \overline B) = (A \cap \overline B) \cup (\overline A \cap B) = D = \{1, 2, 6, 9\},$$

$$F = (A \cup C) \cap \overline B = \{1, 2, 3, 5, 6, 7, 8\} \cap \{1, 2, 4, 5, 7, 8\} = \{1, 2, 5, 7, 8\},$$

$$H = (\bar A \cap \overline C) \cup (A \cap B \cap C) = (\overline A \cap \overline C) \cup \phi = \{4, 9\}.$$

(1)  Only the  proposed solution 2  is correct:

• $A$  and  $C$  have no common element.
• $A$  and  $B$  each contain a  $3$.
• $B$  and  $C$  each contain a  $6$.

(2)  Correct is the  proposed solution 2:

• No digit is contained in  $A$,  $B$  and  $C$  at the same time   ⇒   $ A \cap B \cap C = \phi$   ⇒   $ \overline{A \cap B \cap C} = \overline{\phi} = G$.
• The first proposition, on the other hand,  is wrong.  It is missing a  $4$.

(3)  Correct are the  proposed solutions 1, 2 and 4:

• The first proposal is correct:   The sets  $D$  and  $E$  contain exactly the same elements and thus also their complementary sets.
• The second proposal is also correct:   In general, i.e. for any  $X$  and  $B$  the following holds:  $(X \cap \overline B) \subset \overline B \ \Rightarrow$   With $X = A \cup C$ it follows that $F \subset \overline B$.
• The last proposal is also correct:   $A = \{1, 2, 3\},$  $C = \{5, 6, 7, 8\}$  and  $H = \{4, 9\}$  form a "complete system".
• The third suggestion,  on the other hand,  is wrong because  $B$  and  $C$  are not disjoint.