Exercise 1.6Z: Ergodic Probabilities

• Return to book

Markov chain with  $A$,  $B$

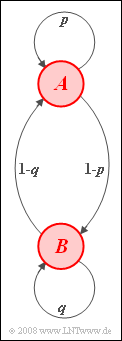
We consider a homogeneous stationary first-order Markov chain with events  $A$  and  $B$  and transition probabilities corresponding to the adjacent Markov diagram:

For subtasks  (1)  to  (4),  assume:

• Event  $A$  is followed by  $A$  and  $B$  with equal probability.

• After  $B$:  The event  $A$  is twice as likely as  $B$.

From subtask  (5)  on,  $p$  and  $q$  are free parameters,  while the ergodic probabilities  ${\rm Pr}(A) = 2/3$  and  ${\rm Pr}(B) = 1/3$  are fixed.

Hints:

• The exercise belongs to the chapter  Markov Chains.

• You can check your results with the   (German language)  interactive SWF applet

Ereigniswahrscheinlichkeiten einer Markov-Kette erster Ordnung   ⇒   "Event Probabilities of a First Order Markov Chain".

Questions

1

What are the transition probabilities  $p$  and  $q$?

$p \ = \ $

$q \ = \ $

2

Calculate the ergodic probabilities.

${\rm Pr}(A) \ = \ $

${\rm Pr}(B) \ = \ $

3

What is the conditional probability that event  $B$  occurs if event  $A$  occurred two steps before?

${\rm Pr}(B_{\nu}\hspace{0.05cm}|\hspace{0.05cm}A_{\nu-2})\ = \ $

4

What is the inferential probability that event  $A$  occurred two steps before,  when event  $B$  currently occurs?

${\rm Pr}(A_{\nu-2}\hspace{0.05cm}|\hspace{0.05cm}B_{\nu})\ = \ $

5

Let now  $p = 1/2$  and  ${\rm Pr}(A) = 2/3$.  Which value results for  $q$?

$q\ = \ $

6

How must the parameters be chosen so that the sequence elements of the Markov chain are statistically independent and additionally  ${\rm Pr}(A) = 2/3$ ?

$p \ = \ $

$q \ = \ $

Solution

Solution

(1)  According to the instruction,   $p = 1 - p$   ⇒   $\underline{p =0.500}$  and  $q = (1 - q)/2$,   ⇒   $\underline{q =0.333}$  holds.

(2)  For the event probability of  $A$  holds:

$${\rm Pr}(A) = \frac{{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)}{{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)+{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A)} = \frac{1-q}{1-q+1-p} = \frac{2/3}{2/3 + 1/2}= \frac{4}{7} \hspace{0.15cm}\underline {\approx0.571}.$$

• This gives  ${\rm Pr}(B)= 1 - {\rm Pr}(A) = 3/7 \hspace{0.15cm}\underline {\approx 0.429}$.

(3)  No statement is made about the time  $\nu-1$ . 

• At this time  $A$  or  $B$  may have occurred. Therefore holds:

$${\rm Pr}(B_{\nu} \hspace{0.05cm} | \hspace{0.05cm}A_{\nu -2}) = {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.05cm} \cdot \hspace{0.05cm}{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.15cm} +\hspace{0.15cm} {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.05cm} \cdot \hspace{0.05cm}{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}B) = p \hspace{0.1cm} \cdot \hspace{0.1cm} (1-p) + q \hspace{0.1cm} \cdot \hspace{0.1cm} (1-p) = {5}/{12} \hspace{0.15cm}\underline {\approx 0.417}.$$

(4)  According to Bayes' theorem:

$${\rm Pr}(A_{\nu -2} \hspace{0.05cm} | \hspace{0.05cm}B_{\nu}) = \frac{{\rm Pr}(B_{\nu} \hspace{0.05cm} | \hspace{0.05cm}A_{\nu -2}) \cdot {\rm Pr}(A_{\nu -2} ) }{{\rm Pr}(B_{\nu}) } = \frac{5/12 \cdot 4/7 }{3/7 } = {5}/{9} \hspace{0.15cm}\underline {\approx 0.556}.$$

Reasoning:

• The probability  ${\rm Pr}(B_{\nu}\hspace{0.05cm}|\hspace{0.05cm}A_{\nu-2})= 5/12$  has already been calculated in subsection  (3).
• Due to stationarity,  ${\rm Pr}(A_{\nu-2})= {\rm Pr}(A) = 4/7$  and  ${\rm Pr}(B_{\nu})= {\rm Pr}(B) = 3/7$  holds.
• Thus,  the value of  $5/9$ is obtained for the sought inference probability according to the above equation.

(5)  According to subtask  (2)  with  ${p =1/2}$  for the probability of  $A$  in general:

$${\rm Pr}(A) = \frac{1-q}{1.5 -q}.$$

• Thus from  $ {\rm Pr}(A) = 2/3$  follows  $\underline{q =0}$.

(6)  In the case of statistical independence,  for example,  it must hold:

$${{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A)} = {{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)} = {{\rm Pr}(A)}.$$

• From this follows  $p = {\rm Pr}(A) \hspace{0.15cm}\underline {= 2/3}$  and accordingly  $q = 1-p \hspace{0.15cm}\underline {= 1/3}$.