Exercise 2.2: Properties of Galois Fields
Here we consider the sets of numbers
- $Z_5 = \{0, \, 1, \, 2, \, 3, \, 4\} \ \Rightarrow \ q = 5$,
- $Z_6 = \{0, \, 1, \, 2, \, 3, \, 4,\, 5\} \ \Rightarrow \ q = 6$.
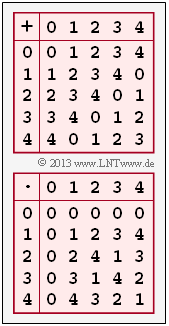
In the adjacent graph, the (partially incomplete) addition and multiplication tables for $q = 5$ and $q = 6$ are given, where both addition ("$+$") and multiplication ("$\hspace{0.05cm}\cdot\hspace{0.05cm}$") modulo $q$ are to be understood.
To be checked is whether the number sets $Z_5$ and $Z_6$ satisfy all the conditions of a Galois field $\rm GF(5)$ and $\rm GF(6)$, respectively.
In the "theory section" a total of eight conditions are mentioned, all of which must be met. You are to check only two of these conditions:
$\rm(D)$ For all elements there is an additive inverse (Inverse for "$+$"):
- $$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_A}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i + {\rm Inv_A}(z_i) = 0 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_A}(z_i) = -z_i \hspace{0.05cm}.$$
$\rm(E)$ All elements have a multiplicative inverse (Inverse for "$\hspace{0.05cm}\cdot\hspace{0.05cm}$"):
- $$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} z_i \ne 0, \hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_M}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i \cdot {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = z_i^{-1}\hspace{0.05cm}.$$
The other conditions for a Galois field, viz.
- Closure,
- Existence of zero– and identity element,
- validity of commutative law, associative law and distributive law
are satisfied by both, $Z_5$ and $Z_6$.
Hints: The exercise refers to the chapter "Some Basics of Algebra".
Questions
Solution
- $$A_{04} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 4}\hspace{0.05cm},\hspace{0.2cm}A_{14}=(1+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm}A_{24}=(2+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm},$$
- $$A_{34} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (3+4)\hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5= 2\hspace{0.05cm},\hspace{0.2cm}A_{44}=(4+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 3}\hspace{0.05cm}.$$
Due to the commutative law of addition,
- $$z_i + z_j = z_j + z_i \hspace{0.5cm} {\rm for \hspace{0.2cm}all\hspace{0.2cm} } z_i, z_j \in Z_5\hspace{0.05cm},$$
the last column of the addition table is of course identical to the last row of the same table.
(2) Now $M_{\mu 4} = (\mu \cdot 4) \, {\rm mod} \, 5$ and we obtain:
- $$M_{04} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm}M_{14}=(1\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 4}\hspace{0.05cm},\hspace{0.2cm}M_{24}=(2\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 3\hspace{0.05cm},$$
- $$M_{34} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (3\cdot4)\hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2\hspace{0.05cm},\hspace{0.2cm}M_{44}=(4\cdot 4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 1}\hspace{0.05cm}.$$
Since multiplication is also commutative, the last column in the multiplication table again matches the last row.
(3) The graph shows the full addition and multiplication tables for $q = 5$. You can see:
- In the addition table there is exactly one zero in each row (and also in each column).
- So for every $z_i ∈ Z_5$ there is an ${\rm Inv}_{\rm A} (z_i)$ that satisfies the condition $[z_i + {\rm Inv}_{\rm A}(z_i)] \, {\rm mod} \, 5 = 0$:
- $$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = 0 \hspace{0.05cm},$$
- $$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-1) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4 \hspace{0.05cm},$$
- $$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-2) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 3 \hspace{0.05cm},$$
- $$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 3\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-3) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2 \hspace{0.05cm},$$
- $$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm}.$$
- In the multiplication table we leave the zero element (first row and first column) out of consideration.
- In all other rows and columns of the lower table there is indeed exactly one each.
- From the condition $[z_i \cdot {\rm Inv}_{\rm M}(z_i)] \, {\rm mod} \, 5 = 1$ one obtains:
- $$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 1\hspace{0.05cm},$$
- $$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 3 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 6 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm},$$
- $$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 3 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 2 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 6 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm},$$
- $$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 4 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm}.$$
- Since both the required additive and multiplicative inverses exist ⇒ $Z_5$ describes a Galois field $\rm GF(5)$
- Correct is the proposed solution 1.
(4) From the blue addition table on the statement page, we see that all numbers $(0, \, 1, \, 2, \, 3, \, 4, \, 5)$ of the set $Z_6$ have an additive inverse
⇒ in each row (and column) there is exactly one zero.
- On the other hand, a multiplicative inverse ${\rm Inv}_{\rm M}(z_i)$ exists only for $z_i = 1$ and $z_i = 5$, viz.
- $$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 1\hspace{0.05cm},$$
- $$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 5 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 5 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 25 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 6 = 1 \hspace{0.05cm}.$$
- For $z_i = 2, \ z_i = 3$ and $z_i = 4$, we find no element $z_j$, so that $(z_i \cdot z_j) \, {\rm mod} \, 6 = 1$.
- Correct is the proposed solution 3 ⇒ the blue tables for $q = 6$ do not yield a Galois field $\rm GF(6)$.
(5) Correct is the proposed solution 2:
- A finite number set $Z_q = \{0, \, 1, \hspace{0.05cm} \text{...} \hspace{0.1cm} , \, q-1\}$ of natural numbers leads to a Galois field only if $q$ is a prime number.
- Of the number sets mentioned above, this is true only for $Z_{11}$.