Exercise 2.9: Huffman Decoding after Errors

• Return to book

Overall system with "Huffman"

We consider Huffman coding according to the following assignment:

  $\rm A$   →   1,     $\rm B$   →   01,     $\rm C$   →   001,     $\rm D$   →   000.

Huffman coding is always  lossless.  This means:

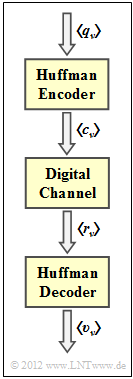
• If the encoded sequence  $\langle c_\nu \rangle$  is immediately decoded again after the Huffman encoder, the decoding result  $\langle v_\nu \rangle$  is equal to the source symbol sequence  $\langle q_\nu \rangle$.

• If, on the other hand, the reception sequence  $\langle r_\nu \rangle$   does not match the generated code sequence  $\langle c_\nu \rangle$  due to errors during transmission 
  $($0   →   1,     1   →   0$)$, error propagation may occur.
• A single bit error can then lead to (almost) all subsequent characters being decoded incorrectly.

Hints:

• The exercise belongs to the chapter  Entropy coding according to Huffman.
• In particular, reference is made to the page  Influence of transmission errors on decoding .

Questions

1

We consider the encoded sequence  $\langle c_\nu \rangle = \rm \langle 10100100011000010011 \rangle$.  What is the corresponding source symbol sequence?

	$\langle q_\nu \rangle = \rm \langle \rm CCDAADBCA \rangle$,
	$\langle q_\nu \rangle = \rm \langle\rm ABDDAADBCA \rangle$,
	$\langle q_\nu \rangle = \rm \langle\rm ABCDAADBCA \rangle$,
	Other than the three above.

2

Which sequence  $\langle v_\nu \rangle$  results after decoding if the first bit is falsified  $\rm (1   →   0)$?
    $\langle c_\nu \rangle = \rm \langle 10100100011000010011 \rangle$     ⇒     $\langle r_\nu \rangle = \rm \langle \underline{0}0100100011000010011 \rangle$.

	$\langle v_\nu \rangle = \rm \langle \rm CCDAADBCA \rangle$,
	$\langle v_\nu \rangle = \rm \langle\rm ABDDAADBCA \rangle$,
	$\langle v_\nu \rangle = \rm \langle\rm ABCDAADBCA \rangle$,
	One other than the three mentioned.

3

Is it possible that by another bit error the later symbols will all be decoded correctly again?

	Yes, by a second bit error at position 2.
	Yes, by a second bit error at position 10.
	Yes, by a second bit error at position 15.
	No.

4

Which sequence  $\langle v_\nu \rangle$  results after decoding if the sixth bit is falsified  $\rm (1   →   0)$?
    $\langle c_\nu \rangle = \rm \langle 10100100011000010011 \rangle$   ⇒   $\langle r_\nu \rangle = \rm \langle 10100\underline{0}00011000010011 \rangle$.

	$\langle v_\nu \rangle = \rm \langle \rm CCDAADBCA \rangle$,
	$\langle v_\nu \rangle = \rm \langle\rm ABDDAADBCA \rangle$,
	$\langle v_\nu \rangle = \rm \langle\rm ABCDAADBCA \rangle$,
	A different one from the three mentioned.

Solution

Solution

(1) Solution suggestion 3 is correct:

• Below you can see the encoded sequence divided by inverted commas:

$$\langle c_\nu \rangle = \rm \langle 1'01'001'000'1'1'000'01'001'1 \rangle .$$

• This belongs to the following source symbol sequence:

$$\langle q_\nu \rangle = \rm \langle ABCDAADBCA \rangle .$$

(2) Solution suggestion 1 is correct:

• With a bit error at position 1, one obtains for the reception sequence:

$$\langle r_\nu \rangle = \rm \langle 00100100011000010011 \rangle .$$

• The inverted commas clarify the individual blocks of decoding:

$$\langle r_\nu \rangle = \rm \langle 001'001'000'1'1'000'01'001'1 \rangle .$$

• This leads to the following sink symbol sequence:

$$\langle v_\nu \rangle = \rm \langle CCDAADBCA \rangle .$$

Interpretation:

• $\rm AB$  is replaced by  $\rm C$ , the further text  $\rm CDAADBCA$  is unchanged, but shifted by one position.
• However, if you compare the first nine symbols of the original with the decoding result  position by position, as an automaton would do, you will recognise eight different symbols.

(3)  The correct answers are 1 and 3:

• An additional bit error at position 2  $\rm (0   →   1)$  falsifies  $\rm AB$  to  $\rm BA$,  but all further symbols are recognised correctly again.
• An additional bit error at position 15  $\rm (0   →   1)$  leads to

$$\langle r_\nu \rangle = \rm {\langle \underline{0}01'001'000'1'1'000'\underline{1}'1'001'1 \rangle} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\langle \it v_\nu \rangle = \rm \langle \underline{C}CDAAD\underline{AA}CA \rangle .$$

Due to the bit error at position 1  $\rm (1   →   0)$ ,   $\rm AB$  is falsified to  $\rm C$ , i.e. a character is  "swallowed".  The additional bit error at position 15  $\rm (0   →   1)$  turns  $\rm B$  into the tuple  $\rm AA$.  After that, all symbols in the correct position are recognised correctly, starting with  $\rm CA$.

• An additional bit error at position 10  $\rm (1   →   0)$  on the other hand, leads to

$$\langle r_\nu \rangle = \rm \langle \underline{0}01'001'000'\underline{0}'1'000'0'1'001'1 \rangle \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\langle \it v_\nu \rangle = \rm \langle \underline{C}CDAAD\underline{B}CA \rangle .$$

The bit error at position 10 turns  $\rm AA$  into  $\rm B$.  The decoder thus swallows a total of two characters.  All subsequently decoded characters are then not in the correct position.

(4) Solution suggestion 2 is correct:

• The first bit error at position 6  $\rm (1   →   0)$  yields

$$\langle r_\nu \rangle = \rm \langle 101'00\underline{0}'000'1'000'0'1'001'1 \rangle \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\langle \it v_\nu \rangle = \rm \langle AB\underline{D}DAADBCA \rangle .$$

• The first  $\rm C$  becomes a  $\rm D$.  All other symbols are decoded correctly.