Exercise 4.09Z: Periodic ACF

• Return to book

Periodic multilevel rectangular signal

We consider in this exercise a periodic and simultaneously ergodic stochastic process  $\{x_i(t)\}$,  which is fully characterized by the presented pattern function  $x(t)$.

Further pattern signals of the random process  $\{x_i(t)\}$  are obtained by shifting by different delays  $\tau_i$,  where  $\tau_i$  is assumed to be uniformly distributed between  $0$  and the period  $T_0$.

Hint:  The exercise belongs to the chapter  Auto-Correlation Function.

Questions

1

Determine the period duration  $T_0$  normalized to the period duration  $T$  defined in the sketch.

$T_0/T \ = \ $

2

What is the size of the DC signal component   ⇒   linear mean  $m_x$  of the described process  $\{x_i(t)\}$?

$m_x \ = \ $ $\ \rm V$

3

What is the process power  (related to the resistor  $1 \hspace{0.05cm} \rm \Omega$ )?

$P_x \ = \ $ $\ \rm V^2$

4

Calculate the ACF values for  $\tau = T$  and  $\tau = 2T$.

$\varphi_x(\tau = T) \ = \ $ $\ \rm V^2$

$\varphi_x(\tau = 2T) \ = \ $ $\ \rm V^2$

5

Sketch the ACF curve taking into account symmetries.  What values result for  $\tau = 3T$  and  $\tau = 4T$?

$\varphi_x(\tau = 3T) \ = \ $ $\ \rm V^2$

$\varphi_x(\tau = 4T)\ = \ $ $\ \rm V^2$

6

Calculate the expected value of the ACF with respect to all  $\tau$ values.  Interpret the result.

${\rm E}\big[\varphi_x(\tau)\big]\ = \ $ $\ \rm V^2$

Solution

Solution

For the ACF calculation

(1)  The  (normalized)  period duration is  $T_0/T \hspace{0.15cm}\underline{= 5}.$

(2)  Due to periodicity,  the averaging over a periodic time  $T_0$:

$$m_x = \frac{1}{T_0} \cdot \int_0^{T_0} x(t) \hspace{0.1cm}{\rm d} t = \frac{1}{5 T} \cdot (2\hspace{0.05cm}{\rm V} \cdot 2 T - 2\hspace{0.05cm}{\rm V} \cdot 2 T) \hspace{0.15cm}\underline{= \rm 0.4 \,V}.$$

(3)  In analogy to the last subtask,  we obtain for the mean power:

$$P_x = \frac{2 T}{5 T} \cdot \big[(\rm 2V)^2 +(- \rm 1V)^2 \big]\hspace{0.15cm}\underline{ = \rm 2 \,V^2}.$$

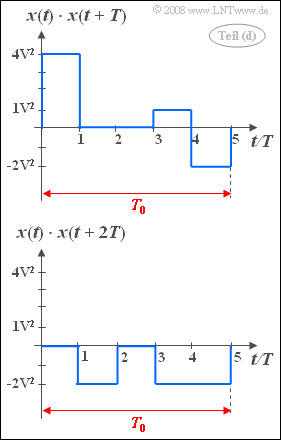
(4)  The accompanying graph shows in each case in the range from  $0$  to  $T_0 = 5T$.

• above the product  $x(t) \cdot x(t+T)$,
• down the product  $x(t) \cdot x(t+2T)$.

• Note that  $x(t+T)$  means a shift of the signal  $x(t)$  by  $T$  to the left.

• From these sketches follow the relations:

$$\varphi_x (T)= \rm {1}/{5 } \cdot (\rm 4V^2 + \rm 1V^2 - \rm 2V^2) \hspace{0.15cm}\underline{= \rm 0.6\, V^2},$$

$$\varphi_x ( 2 T)= \rm {1}/{5 } \cdot(-\rm 2V^2 \cdot 3) \hspace{0.15cm}\underline{= - \rm 1.2 \,V^2}.$$

Wanted auto-correlation function

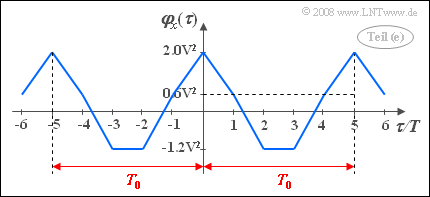
(5)  An auto-correlation function is always even:  

$$\varphi_x (-\tau)= \varphi_x (\tau).$$

• In addition,  for periodic processes,  the ACF is also periodic with the same period duration  $T_0$  as the individual pattern functions.  It follows that:

$$\varphi_x ( 0) = \varphi_x (5 T) = \varphi_x (10 T) = \ \text{...} \ = \it P_x = \rm 2 \,V^2,$$

$$\varphi_x (3 T) = \varphi_x (-3 T) =\varphi_x (2 T) = \ \text{...} \ \hspace{0.15cm}\underline{= - \rm 1.2 \,V^2},$$

$$\varphi_x (4 T) = \varphi_x (-4 T) =\varphi_x ( T) = \ \text{...} \ \hspace{0.15cm}\underline{= \rm 0.6 \,V^2}.$$

• The calculated ACF values can be connected by straight line sections,  since integration over rectangular functions always yields linear subsections.

(6)  The five intervals  $(0$ to $T)$,  $(T$ to $2T)$, ... ,  $(4T$ to $5T)$  provide the contributions.

$$(+1.3; -0.3; -1.2; -0.3; +1.3) \cdot \rm V^2.$$

• This gives the expected value  (linear mean):

$${\rm E}\big[\varphi_x(\tau)\big] = 1/5 \cdot (1.3-0.3 -1.2 -0.3 +1.3]\hspace{0.15cm}\underline{= \rm 0.16 \,V^2}.$$

• This corresponds to the square of the mean  $m_x$   ⇒   see subtask  (2).