Exercise 4.2Z: Mixed Random Variables

PDF of

$X$ (top), and
CDF of

$Y$ (bottom)

One speaks of a "mixed random variable", if the random variable contains discrete components in addition to a continuous component.

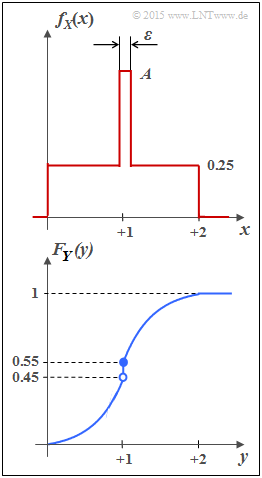
For example, the random variable $Y$ with cumulative distribution function $F_Y(y)$ as shown in the sketch below has both a continuous and a discrete component.
The probability density function $f_Y(y)$ is obtained from $F_Y(y)$ by differentiation.
The jump at $y= 1$ in the CDF thus becomes a "Dirac" in the probability density function.

In subtask (4) the differential entropy $h(Y)$ of $Y$ is to be determined (in bit), assuming the following equation:

$h(Y) = \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm log}_2 \hspace{0.1cm} \big[ f_Y(y) \big] \hspace{0.1cm}{\rm d}y \hspace{0.05cm}.$

In subtask (2), calculate the differential entropy $h(X)$ of the random variable $X$ whose PDF $f_X(x)$ is sketched above. If one performs a suitable boundary transition, the random variable $X$ also becomes a mixed random variable.

Hints:

The exercise belongs to the chapter Differential Entropy.
Further information on mixed random variables can be found in the chapter Cumulative Distribution Function of the book "Theory of Stochastic Signals".

Questions

Solution

(1) Proposed solution 2 is correct because the integral

$1$ over the PDF must yield:

$f_X(x) \hspace{0.1cm}{\rm d}x = 0.25 \cdot 2 + (A - 0.25) \cdot \varepsilon \stackrel{!}{=} 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}(A - 0.25) \cdot \varepsilon \stackrel{!}{=} 0.5 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} A = 0.5/\varepsilon +0.25\hspace{0.05cm}.$

(2) The differential entropy (in "bit") is given as follows:

$h(X) = \hspace{0.1cm} \hspace{-0.45cm} \int\limits_{{\rm supp}(f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{f_X(x)} \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$

We now divide the integral into three partial integrals:

$h(X) = \hspace{-0.25cm} \int\limits_{0}^{1-\varepsilon/2} \hspace{-0.15cm} 0.25 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.25} \hspace{0.1cm}{\rm d}x + \hspace{-0.25cm}\int\limits_{1+\varepsilon/2}^{2} \hspace{-0.15cm} 0.25 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.25} \hspace{0.1cm}{\rm d}x + \hspace{-0.25cm}\int\limits_{1-\varepsilon/2}^{1+\varepsilon/2} \hspace{-0.15cm} \big [0.5/\varepsilon + 0.25 \big ] \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.5/\varepsilon + 0.25} \hspace{0.1cm}{\rm d}x$

$\Rightarrow \hspace{0.3cm} h(X) = 2 \cdot 0.25 \cdot 2 \cdot (2-\varepsilon) - (0.5 + 0.25 \cdot \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm}(0.5/\varepsilon +0.25) \hspace{0.05cm}.$

In particular, one obtains

for $\varepsilon = 0.1$ :

$h(X) =1.9 - 0.525 \cdot {\rm log}_2 \hspace{0.1cm}(5.25) = 1.9 - 1.256 \hspace{0.15cm}\underline{= 0.644\,{\rm bit}} \hspace{0.05cm},$

for $\varepsilon = 0.01$ :

$h(X) =1.99 - 0.5025 \cdot {\rm log}_2 \hspace{0.1cm}(50.25)= 1.99 - 2.84 \hspace{0.15cm}\underline{= -0.850\,{\rm bit}} \hspace{0.05cm}$

for $\varepsilon = 0.001$ :

$h(X) =1.999 - 0.50025 \cdot {\rm log}_2 \hspace{0.1cm}(500.25) = 1.999 - 8.967 \hspace{0.15cm}\underline{= -6.968\,{\rm bit}} \hspace{0.05cm}.$

(3) All the proposed solutions $1$ are correct:

After the boundary transition $\varepsilon → 0$ we obtain for the differential entropy

$h(X) = \lim\limits_{\varepsilon \hspace{0.05cm}\rightarrow \hspace{0.05cm} 0} \hspace{0.1cm}\big[(2-\varepsilon) - (0.5 + 0.25 \cdot \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm}(0.5/\varepsilon +0.25)\big] = 2\,{\rm bit} - 0.5 \cdot \lim\limits_{\varepsilon \hspace{0.05cm}\rightarrow \hspace{0.05cm} 0}\hspace{0.1cm}{\rm log}_2 \hspace{0.1cm}(0.5/\varepsilon) \hspace{0.3cm}\Rightarrow\hspace{0.3cm} - \infty \hspace{0.05cm}.$

PDF and CDF of the mixed random variable

$X$

The probability density function (PDF) in this case is given by.

$f_X(x) = \left\{ \begin{array}{c} 0.25 + 0.5 \cdot \delta (x-1) \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} 0 \le x \le 2, \\ {\rm sonst} \\ \end{array} \hspace{0.05cm}.$

Consequently, it is a "mixed" random variable with

a stochastic, uniformly distributed part in the range $0 \le x \le 2$ , and
a discrete component at $x = 1$ with probability $0.5$ .

The graph shows the PDF $f_X(x)$ on the left and the CDF $F_X(x)$ on the right.
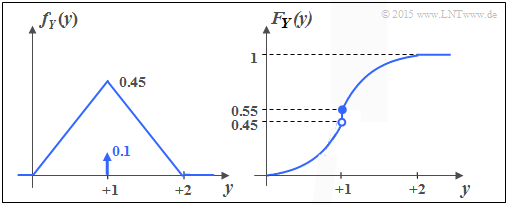
(4) The correct solutions are 2, 3 and 5. The lower graph shows the PDF and the CDF of the random variable $Y$ . You can see:

PDF and CDF of the mixed random variable

$Y$

Like $X$ , $Y$ contains a continuous and a discrete part.
The discrete part occurs with probability ${\rm Pr}(Y = 1) = 0.1$ .
Since $F_Y(y)= {\rm Pr}(Y \le y)$ holds, the right-hand side limit is:

$F_Y(y = 1) = 0.55.$

The continuous component is not uniformly distributed; rather, there is a triangular PDF.
The last proposition is also correct: $h(Y) = h(X) = - \infty$ .

Because: For every random quantity with a discrete part – and it is also extremely small, the differential entropy is equal minus infinity..

	The CDF value at the point $y = 1$ is $0.5$ .
	$Y$ contains a discrete and a continuous component.
	The discrete component at $Y = 1$ occurs with $10\%$ probability.
	The continuous component of $Y$ is uniformly distributed.
	The differential entropies of $X$ and $Y$ are equal.

	$A = 0.5/\varepsilon$ ,
	$A = 0.5/\varepsilon+0.25$ ,
	$A = 1/\varepsilon$ .

	$f_X(x)$ now has a continuous and a discrete component.
	The differential energy $h(X)$ is negative.
	The magnitude $\|h(X)\|$ is infinite.