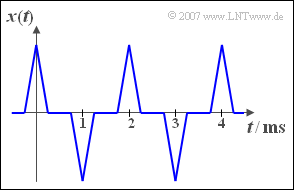
The graph shows the periodic signal $x(t)$. If $x(t)$ is applied to the input of a non-linearity with the characteristic curve
- $$y=g(x)=\left\{ {x \; \rm for\; \it x \geq \rm 0, \atop {\rm 0 \;\;\; \rm else,}}\right.$$
the signal $y(t)$ is obtained at the output. A second non-linear characteristic
- $$z=h(x)=|x|$$
delivers the signal $z(t)$.
Note:
- This exercise belongs to the chapter General description of periodic signals.
Questions
Solution
(1) Correct are the solutions 1 and 4:
- The non-linear characteristic $y = g(x)$ describes a half-wave rectifier.
- $z = h(x) = |x|$ describes a full-wave rectifier.
(2) The period duration $x(t)$ is $T_0 = 2\,\text{ms}$. The inverse magnitudes to the base frequency $f_0 \hspace{0.1cm}\underline{ = 500\,\text{Hz}}$.
(3) The half-wave rectification does not change the duration of the period, see the left graph: $T_0 \hspace{0.1cm}\underline{= 2\,\text{ms}}$.
(4) After full-wave rectification, the signal $z(t)$ has double the frequency (see right graph). The following values apply here:
- $$T_0 = 1\,\text{ms}, \hspace{0.5cm} f_0 = 1\,\text{kHz}, \hspace{0.5cm} \omega_0 \hspace{0.1cm}\underline{= 6283\,\text{1/s}}.$$