Exercise 2.1Z: DSB-AM without/with Carrier

• Return to book

The signals involved in this AM

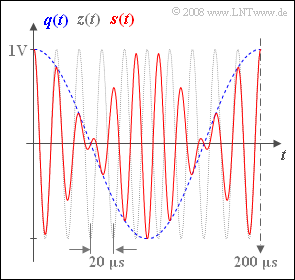
The red curve on the graph shows a section of the transmitted signal  $s(t) = q(t) · z(t)$  of a double-sideband amplitude modulation  (abbreviated as DSB-AM)  without carrier.  The duration of the time interval is  $\rm 200 \ µ s$.

Additionally plotted in the graph are:

• the source signal  (as a blue dashed curve):

$$q(t) = 1\,{\rm V} \cdot \cos(2 \pi f_{\rm N} t + \phi_{\rm N}),$$

• the carrier signal  (as a grey dashed trace):

$$z(t) = 1 \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T}).$$

From subtask  (4)  onwards,  the "DSB-AM with carrier"  is considered.  In that case, with  $A_{\rm T} = 2\text{ V}$:

$$s(t) = \left(q(t) + A_{\rm T} \right) \cdot z(t) \hspace{0.05cm}.$$

Hints:

• This exercise belongs to the chapter  Double-Sideband Amplitude Modulation.
• Particlar reference is made to the pages  Description in the time domain  and  Double-Sideband Amplitude Modulation with carrier.

Questions

1

From the graph,  determine the phase values of the message and carrier signals.

$\phi_{\rm N} \ = \ $ $\ \text{degrees}$

$\phi_{\rm T} \ = \ $ $\ \text{degrees}$

2

What is the frequency $f_{\rm N}$  of the message signal  $q(t)$  and what is the frequency $f_{\rm T}$  of the carrier signal  $z(t)$?

$f_{\rm N} \ = \ $ $\ \text{kHz}$

$f_{\rm T} \ = \ $ $\ \text{kHz}$

3

Analyze the zero crossings of  $s(t)$.  Which statements are true?

	All zero crossings of  $z(t)$  are preserved in  $s(t)$.
	There are additional zero crossings caused by  $q(t)$.
	$s(t) = a(t) · \cos(ω_T · t)$  holds with  $a(t) = |q(t)|$.

4

Determine the spectral function  $S(f)$  by convolution.  Which  (positive)  frequencies  $f_1$  and  $f_2 > f_1$  are included in the signal??

$f_1 \ = \ $ $\ \text{kHz}$

$f_2\ = \ $ $\ \text{kHz}$

5

Let  $A_{\rm T} = 2\text{ V}$.  What is the modulation depth  $m$?

$m \ = \ $

6

Which of the statements are true for   "DSB–AM with carrier"  and  $A_{\rm T} = 2\text{ V}$ ?

	$S(f)$  now includes Dirac delta functions at  $±f_{\rm T}$.
	The weights of these Dirac delta lines are each  $2\text{ V}$.
	$q(t)$  can be seen in the envelope of  $s(t)$.
	Due to the additional carrier component,  the power remains unchanged.

Solution

Solution

(1)  Both signals are cosine   ⇒   $ϕ_{\rm N} \hspace{0.15cm}\underline { = 0}$  and  $ϕ_{\rm T} \hspace{0.15cm}\underline { = 0}$.

(2)  From the graph,  the period durations of   $200$ μs  and   $20$ μs   can be seen for  $q(t)$  and $z(t)$,  respectively.

• This gives the frequencies as   $f_{\rm N} \hspace{0.15cm}\underline { = 5}$  kHz and  $f_{\rm T} \hspace{0.15cm}\underline { = 50}$ kHz.

(3)  Answers 1 and 2  are correct:

• The zero crossings of  $z(t)$  at  $±5$ μs,  $±15$ μs,  $±25$ μs, ... ... are also present in the signal  $s(t)$    ⇒   Answer 1 is correct.
• Other zero intersects of  $s(t)$ – cause by  $q(t)$  – are present at  $±50$ μs,  $±150$ μs,  $±250$ μs, ....   ⇒   Answer 2 is also correct.
• In contrast, the third statement is not true. Instead,   $s(t) = a(t) \cdot \cos[\omega_{\rm T} t + \phi (t)] \hspace{0.05cm}.$

DSB–AM spectra  $Z(f)$,  $Q(f)$  and  $S(f)$

• For  $q(t) > 0$  the phase function is  $ϕ(t) = 0$  and  $s(t)$  coincides with   $z(t)$.
• In contrast, for  $q(t) < 0$:   $ϕ(t) = π = 180^\circ$.
• At the zero crossings of  $q(t)$,  the modulated signal   $s(t)$  exhibits phase jumps.

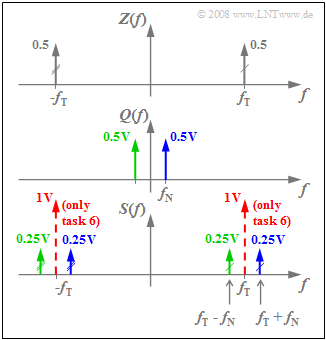
(4)  The spectrum  $S(f)$  results from the convolution of the spectral functions   $Z(f)$  and  $Q(f)$,  each consisting of only two Dirac delta functions.  The graph displays the result.

• The Dirac delta functions plotted in red apply only to the  "DSB-AM with carrier"  and refer to subtask (6).
• Convolution of the two  $Z(f)$  Dirac delta functions at  $f_{\rm T} = 50\text{ kHz}$  with  $Q(f)$  leads to the Dirac delta lines at  $f_{\rm T} - f_{\rm N}$  and  $f_{\rm T} + f_{\rm N}$,  each with weight   $0.5 · 0.5\text{ V}= 0.25\text{ V}$.
• Thus,  the desired values are   $f_1\hspace{0.15cm}\underline { = 45 \ \rm kHz}$  and  $f_1\hspace{0.15cm}\underline { = 55 \ \rm kHz}$.
• The Dirac function  $0.5 · δ(f + f_{\rm T})$  with two markers leads to two more Dirac delta lines at   $-f_1$  and  $-f_2$.

(5)  The modulation depth is calculated as:

$$m = \frac{q_{\rm max}}{A_{\rm T}} = \frac{A_{\rm N}}{A_{\rm T}} \hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$

(6)  Answers 1 and 3  are correct:

• According to the sketch,  Dirac delta lines result at   $±f_{\rm T}$,  both with impulse weight  $A_{\rm T}/2 = 1\text{ V}$.
• At  $m ≤ 1$,  $q(t)$  is detectable in the envelope   ⇒   envelope demodulation is applicable.
• However,  this simpler receiver variant must be accounted for with a much larger transmission power.  
• In this example  $(m = 0.5)$  the addition of a carrier multiplies the transmission power by nine.