Exercise 3.09: Basics of the Viterbi Algorithm
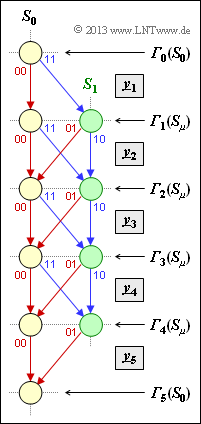
The graph shows a trellis diagram and simultaneously defines the cumulative error values $($"metrics"$)$ ${\it \Gamma}_i(S_0)$ and ${\it \Gamma}_i(S_1)$ at times $i = 0$ to $i = 5$.
From this trellis can be read, for example:
- the code rate $R$,
- the memory $m$,
- the free distance $d_{\rm F}$,
- the information sequence length $L$,
- the sequence length $L\hspace{0.05cm}'$ including the termination.
In the exercise it is further necessary to clarify:
- the meaning of the final error value ${\it \Gamma}_5(S_0)$,
- effects of one and two transmission errors, respectively.
Hint: This exercise belongs to the chapter "Decoding of Convolutional Codes".
Questions
Solution
- There are $2^{k \cdot m} = 2$ states here. It follows that $k = 1$ and $m = 1$.
- Per coding step, $n = 2$ code bits are output ⇒ $R = 1/2$.
- The information sequence length is $L = 4$.
- Only by one $($since $m = 1)$ additional termination bit one arrives at the total length $L' = 5$.
(2) The free distance $d_{\rm F}$ is defined as the number of code bits in which two sequences $\underline{x}$ and $\underline{x'}$ differ.
- We choose the zero sequence as the reference sequence:
- $$\underline{x}\hspace{0.03cm}' = \underline{0} = \big (00\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, ... \hspace{0.1cm} \big ) \hspace{0.05cm},$$
- expressed with the sequence of states: $S_0 → S_0 → S_0 → S_0 → \ \text{...} \ $
- One of the sequences $\underline{x} ≠ \underline{0}$, which differs from $\underline{0}$ only in the minimum number of code bits, follows the path $S_0 → S_1 → S_0 → S_0 → \text{...} \ $:
- $$\underline{x} = \big (11\hspace{0.05cm}, 01\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, ... \hspace{0.1cm} \big ) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} d_{\rm F}\hspace{0.1cm}\underline{ = 3} \hspace{0.05cm}.$$
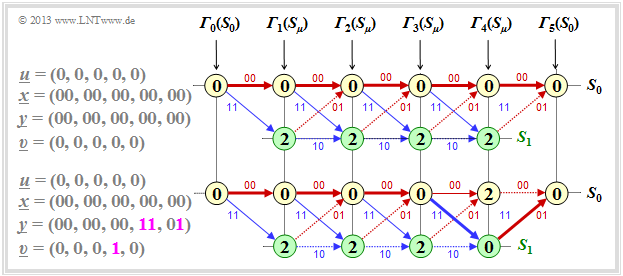
(3) Only proposition 3 is correct here, because the event "No transmission error" is much more likely than three errors at exactly specified positions. Consider the graph:
- If the zero sequence is sent and this is also received, the Viterbi decoding can be illustrated by the upper trellis.
- The final value of the metric is ${\it \Gamma}_5(S_0) = 0$, and the Viterbi decoder decides correctly with certainty: $\underline{z} = \underline{x} ⇒ \underline{v} = \underline{u}$.
- For the lower trellis, we also assume $\underline{u} = (0, \, 0, \, 0, \, 0 \, 0) ⇒ \underline{x} = (00, \, 00, \, 00, \, 00, \, 00)$.
- However, $\underline{y} = (00, \, 00, \, 00, \, 11, \, 01)$ is received now.
- Nevertheless, ${\it \Gamma}_5(S_0) = 0$ holds. The example proves that the first two statements are false.
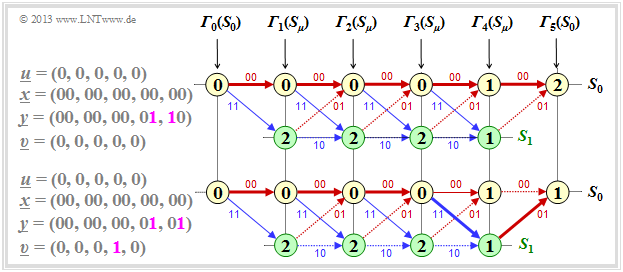
(4) Correct are all answers: If it is known for sure that only one transmission error occurred, for a convolutional code with free distance $d_{\rm F} = 3$ the Viterbi algorithm works perfectly, no matter at which position the error occurred.
(5) None of the proposed solutions is correct, as can be seen from the second graphic.