Exercise 3.10: Noise Power Calculation
Consider the phase and frequency modulation of a cosine oscillation with frequency $f_{\rm N}$. . First, let the message frequency be $f_{\rm N} = f_5 = 5 \ \rm kHz$ and the modulation index (phase deviation) be $η = 5$.
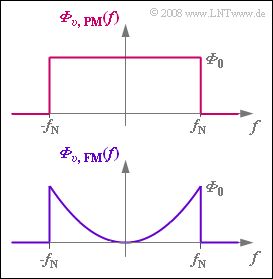
In the presence of additive Gaussian noise with noise power density $N_0$ , the PM demodulator results in a constant noise power density ${\it \Phi}_{v {\rm , \hspace{0.08cm}PM} }(f) = {\it \Phi}_0$, which also depends on the modulation index $η$ :
- $${\it \Phi}_0 = \frac{N_0}{\eta^2} \hspace{0.05cm}.$$
For the calculation of the noise power $P_{\rm R}$ , only the frequency range $±f_{\rm N}$ is relevant (see graph).
The noise power density after FM demodulation with the frequency deviation $Δf_{\rm A}$ is:
- $${\it \Phi}_{v {\rm , \hspace{0.08cm}FM} } (f) = N_0 \cdot \left(\frac{f}{\Delta f_{\rm A}}\right)^2 \hspace{0.05cm}.$$
- The signal-to-noise ratio $10 · \lg ρ_v = 50 \ \rm dB$ is given for phase modulation with $f_{\rm N} = 5 \ \rm kHz$.
- In this task, we are looking for the S/N ratio of FM for the message frequency $f_{\rm N} = 5 \ \rm kHz$ as well as the resulting S/N ratios of PM and FM for message frequency $f_{\rm N} = f_{10} = 10 \ \rm kHz$.
Hints:
- This exercise belongs to the chapter Influence of Noise on Systems with Angle Modulation.
- Particular reference is made to the section System comparison of AM, PM and FM with respect to noise.
Questions
Solution
- $$ \rho_{v } = \frac{P_{\rm S}}{P_{\rm R}} = \frac{P_{\rm S}}{{\it \Phi}_0 \cdot 2 f_{\rm N} } =\frac{\eta^2}{2} \cdot \frac{P_{\rm S}}{N_0 \cdot f_{\rm N} }\hspace{0.05cm}.$$
- The measurement with $f_{\rm N} = f_5 = 5 \ \rm kHz$ gives the SNR $ \rho_{v } = 10^5$ $($corresponding to $10 · \lg ρ_v =50\ \rm dB)$ .
- Doubling the message frequency results in half the SNR, since twice the noise power is now effective:
- $$ \rho_{v }= 0.5 \cdot 10^5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \hspace{0.15cm}\underline {\approx 46.99\,{\rm dB}}\hspace{0.05cm}.$$
This result can also be derived using the relationship $ρ_v = η^2/2 · ξ$ .
- For phase modulation, $η$ is independent of the message frequency.
- DThe SNR loss is due to the fact that now the performance parameter $ξ = P_{\rm S}/(N_0 · f_{\rm N})$ is halved.
(2) For frequency modulation and a message frequency $f_{\rm N} = 5 \ \rm kHz$ the noise power is given by:
- $$P_{\rm R} = \int_{-f_{\rm N}}^{ + f_{\rm N}} {\it \Phi}_{v {\rm , \hspace{0.08cm}FM} } (f)\hspace{0.1cm}{\rm d}f = \frac{2 \cdot N_0}{\Delta f_{\rm A}^{\hspace{0.1cm}2}} \cdot \int_{0}^{ f_{\rm N}} f^2\hspace{0.1cm}{\rm d}f = \frac{2 \cdot N_0 \cdot f_{\rm N}^{\hspace{0.1cm}3}}{3 \cdot \Delta f_{\rm A}^2} \hspace{0.05cm}.$$
- Thus, considering the frequency deviation $Δf_{\rm A} = η · f_{\rm N}$ , we get:
- $$P_{\rm R} = \frac{2 \cdot N_0 \cdot f_{\rm N}}{3 \cdot \eta^2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v }= \frac{3 \cdot \eta^2 \cdot P_{\rm S}}{2 \cdot N_0 \cdot f_{\rm N}} = 3 \cdot \rho_{v {\rm , \hspace{0.08cm}PM}}\hspace{0.05cm}.$$
- This means: frequency modulation is better than phase modulation by a factor of $3$ $($or $4.77 \ \rm dB)$ :
- $$10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v }= 50\,{\rm dB} + 10 \cdot {\rm lg} \hspace{0.15cm}{3}\hspace{0.15cm}\underline {\approx 54.77\,{\rm dB}}\hspace{0.05cm}.$$
(3) According to the answer to question (2) , together with $f_{10} = 10 \ \rm kHz$, we get:
- $$P_{\rm R} = \frac{2 \cdot N_0 \cdot f_{\rm 10}}{3 \cdot \eta_{10}^{\hspace{0.1cm}2}} = \frac{ f_{\rm 10} \cdot \eta_{5}^{\hspace{0.1cm}2}}{ 3 \cdot f_{\rm 5} \cdot \eta_{10}^{\hspace{0.1cm}2}}\cdot \frac{2 \cdot N_0 \cdot f_{\rm 5}}{\eta_{5}^{\hspace{0.1cm}2}} \hspace{0.05cm}.$$
- the second term gives the noise power of the comparison system $($PM, $f_{\rm N} = f_5)$ , which led to the result of $10 · \lg ρ_v = 50\ \rm dB$ .
- However, in frequency modulation, the modulation index $η$ is now inversely proportional to the message frequency, so the quotient is $η_5^2/η_{10}^2 = 4$ .
- Thus, the pre-factor is $8/3$. Due to the larger noise power, the SNR is smaller:
- $$10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v }= 50\,{\rm dB} - 10 \cdot {\rm lg} \hspace{0.15cm}({8}/{3})\hspace{0.15cm}\underline {\approx 45.74\,{\rm dB}}\hspace{0.05cm}.$$
At the same message frequency $f_{\rm N} = 10 \ \rm kHz$ , FM is now $1.25 \ \rm dB$ worse than PM, since the halving of $η$ – a factor of $4$ after squaring– snow has a greater effect than the system-dependent factor of $3$ by which FM was superior to PM.
- The comparison of subtasks (2) and (3) shows a difference by a factor of $8$ and $9.03 \ \rm dB$, respectively.
- The less favorable value for the larger message frequency $f_{\rm N} = 10 \ \rm kHz$ results from the halved modulation index and the doubled large noise bandwidth.