Exercise 3.6Z: Examination Correction

• Return to book

Table for  ${\rm \phi}(x)$  and  ${\rm Q}(x)$

In an exam at the TU Munich  $1000$  students participated.  From the grade  "4.0"  upwards up to  "1.0"  the exam is considered to be passed.  The exam regulations provide for the following grades:

$$1.0, \ 1.3, \ 1.7, \ 2.0, \ 2.3, \ 2.7, \ 3.0, \ 3.3, \ 3.7, \ 4.0, \ 4.3, \ 4.7, \ 5.0.$$

Further,  the exercise must take into account:

• The maximum achievable score is  $100$.  The best student achieved  $88$  points.
• Due to the relatively large number of participants,  the achieved score – this is the random variable  $z$  – has with good approximation a  Gaussian distribution  with mean  $m_z = 60$  and standard deviation  $\sigma_z = 10$.
• In the correction,&nbs

p; not only whole scores were assigned,  but also  (arbitrary)  intermediate  values, so that the random variable  $z$  can be taken as  "continuous valued"  with good approximation.

For scoring,  the guidelines given are:

• Even with six points less than the best  $($so from  $82$  points$)$  one shall get  "1.0".
• If one reaches  $46\%$  of the total score,  one has passed the exam.
• The points/grades assignment shall be linear.

Hints:

• The exercise belongs to the chapter  Gaussian distributed random variables.
• The  "Gaussian distribution"  is often called  "normal distribution".  This is not quite correct:
• A normally distributed random variable  $z$  does have a Gaussian PDF and CDF,  but always with mean  $m_z = 0$  and standard deviation  $\sigma_z = 1$.

Questions

1

What criteria should be considered in problem creation so that the grades will result in  "approximately a normal distribution"?

	There are many exam participants.
	The subproblems depend on each other to a large extent.
	There are many independent problems.
	The exam consists of a single yes/no question.

2

How many examinees are expected to score  "1.0"?

$N_\text{1.0} \ = \ $

3

How many examinees are likely to fail the exam?  Take into account that  $z$  can be taken as a continuous valued random variable.

$N_\text{4.3 ... 5.0} \ = \ $

4

Specify the points/grades assignment.  At what point do you get a  "3.0"?  How many examinees will get this grade?

$N_\text{3.0} \ = \ $

5

How many examinees are expected to receive the grade "2.7"?  Justify why exactly that many examinees will receive the grade  "3.3".

$N_\text{2.7} \ = \ $

6

What will be the mean grade on this exam?  Consider the result of subtask  (5) to solve this subtask.

$\rm mean\hspace{0.15cm}grade \ = \ $

Solution

Solution

(1)  Correct are  the solutions 1 and 3:

• According to the central limit theorem,  a Gaussian distribution is obtained for the sum of many independent quantities.
• Conversely,  if there are only a few dependent tasks,  there is no Gaussian distribution.
• A single yes/no question leads to a two-point distribution  ($0$ points or maximum number of points).
• Even if these imperatives are followed,  a Gaussian distribution will not be expected for very few participants.

(2)  One gets a  "1.0"  with  $82$  points or more. 

• Therefore,  with the mean  $m_z = 60$  and the standard deviation  $\sigma_z = 10$:

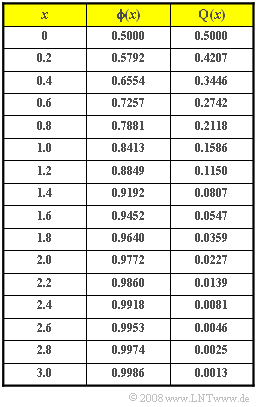
$$\rm Pr(\it z\ge \rm 82)=\rm Q\Bigg(\frac{\rm 82-60}{\rm 10}\Bigg)=\rm Q(\rm 2.2) \hspace{0.15cm}{=\rm 0.0139}.$$

• For a thousand participants,  it follows  $N_\text{1.0}\hspace{0.15cm}\underline{= 14}$.

(3)  With less than  $46$  points, one has failed the exam:

$$\rm Pr(\it z<\rm 46)=\rm Pr(\it z \le \rm 46)=\rm \phi\Bigg(\frac{\rm 46-60}{\rm 10}\Bigg)=\rm \phi(\rm -1.4)=\rm Q(\rm 1.4)=\rm 0.0807.$$

• So  81 students have to compete again.

(4)  The difference in points  $82 - 46 = 36$  must be divided among nine grade intervals  $(1.3$, ... , $4.0)$.

• Each interval thus comprises  $4$  points.
• For example,  one receives a grade of  "3.0"  if one has  $58$  to  $62$  points.
• The probability that the grade is in this range is given by

$$\rm Pr(\rm 58 <\it z<\rm 62)=\rm \phi\Bigg(\frac{\rm 62-60}{\rm 10}\Bigg)-\rm \phi\Bigg(\frac{\rm 58-60}{\rm 10}\Bigg).$$

• Taking advantage of the symmetry,  one obtains:

$$\rm Pr(\rm 58 <\it z<\rm 62) = \rm \phi(\rm 0.2)-\rm \phi(\rm -0.2) = \rm 0.5792-\rm 0.4207=0.1587\hspace{0.2cm}\hspace{0.15cm}\underline{(159 \hspace{0.1cm}\rm participants)}.$$

Notes:

• $z$  is to be taken as a continuous valued random variable. 
• Therefore,  the score  $62$  is simultaneously the upper bound for the grade  "3.0"  as well as the lower bound for the grade  "2.7."
• If  $z$  were only an integer,  then  $62$  would have to be assigned to either the  "2.7"  grade or the  "3.0"  grade,  depending on the mood of the corrector. 
• Of course,  this would have to be done in the same way for all examinees.

(5)  Analogous to the solution of the subtask  (4)  applies to the grade  "2.7":

$$\rm Pr(\rm 62 <\it z<\rm 66)=\rm \phi(\rm 0.6)-\rm \phi(\rm 0.2)=\rm 0.7257-\rm 0.5792=0.1465.$$

• For reasons of symmetry,  the same value is obtained for the grade  "3.3":

$$\rm Pr(\rm 54 <\it z<\rm 58)=\rm \phi(-\rm 0.2)-\rm \phi(-\rm 0.6)= \rm Q(\rm 0.2)-\rm Q(\rm 0.6)=\rm 0.1465.$$

• So  each 146 participants receive a grade of  "2.7"  or  "3.3".

(6)  With the points/grade assignment made here,  not only the points are distributed around  $m_z = 60$  symmetrically,  but also the scores around  "3.0".  There are

• exactly as many  "2.7"s  as  "3.3"s  $($around  $±0.3$  away from  $3.0$ $)$,
• exactly as many  "2.3 "s  as  "3.7"s  $(3.0 ±0.7)$, and
• exactly as many  "1.0 "s  as  "5.0 "s.

Therefore,  the  $\rm mean\hspace{0.15cm} grade\hspace{0.15cm}\underline{ 3.0}$  results.