Exercise 3.7Z: Rectangular Signal with Echo

Transmission signal $s(t)$, and
reception signal $r(t)$ with echo

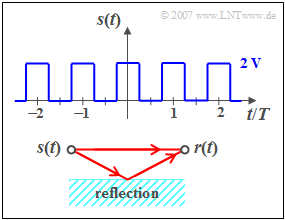
We consider a periodic rectangular signal $s(t)$ with the possible amplitude values $0\text{ V}$ and $2\text{ V}$ and the period duration $T_0 = T = 1 \text{ ms}$. At the jump points, e.g. at $t = T/4$, the signal value are $1\text{ V}$. The DC component $($i.e. the Fourier coefficient $A_0)$ of the signal is $1\text{ V}$, too.

Further applies:

Due to symmetry (even function), all sine coefficients $B_n = 0$.

The coefficients $A_n$ with even $n$ are also zero.

For odd values of $n$, the following applies:

$$A_n = ( { - 1} )^{\left( {n - 1} \right)/2} \cdot \frac{{4\;{\rm{V}}}}{{n \cdot {\rm{\pi }}}}.$$

The signal $s(t)$ reaches the receiver via two paths (see sketch below):

Once on the direct path and secondly via a secondary path.
The latter is characterised by the attenuation factor $\alpha$ and the transit time $\tau$ .
Therefore, the following applies to the received signal:

$$r(t) = s(t) + \alpha \cdot s( {t - \tau } ).$$

The frequency response of the channel is $H(f) = R(f)/S(f)$, the impulse response is denoted by $h(t)$ .

Hints:

This exercise belongs to the chapter The Convolution Theorem and Operation.
Important information can be found on the page Convolution of a function with a Dirac function.

Questions

	For $0 ≤ t < \tau$ holds $h(t) = 1$, and for $t > \tau$ holds $h(t) = 1 + \alpha$.
	It holds that $h(t) = \delta (t) + \alpha \cdot \delta(t - \tau)$.
	$h(t)$ has a Gaussian shape.

$r(t = 0.2 \cdot T)\ = \ $

$\text{V}$

$r(t = 0.3 \cdot T)\ = \ $

$\text{V}$

$r(t = T/2)\ = \ $

$\text{V}$

Solution

(1) The second suggested solution is correct:

The impulse response is equal to the received signal $r(t)$, if a single Dirac delta is present at the input at time $t = 0$ :

$$h(t) = \delta (t) + \alpha \cdot \delta( {t - \tau } ).$$

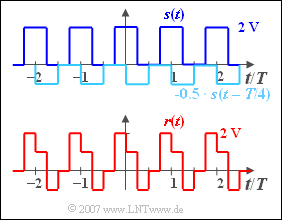
Convolution of square wave signal $s(t)$ and impulse response $h(t)$

(2) It holds $r(t) = s(t) ∗ h(t)$. This convolution operation is most easily performed graphically:

The values of the received signal are generally:

$0.00 < t/T < 0.25\text{:}\hspace{0.4cm} r(t) = +1\hspace{0.02cm}\text{ V}$,
$0.25 < t/T < 0.50\text{:}\hspace{0.4cm} r(t) = -1 \hspace{0.02cm}\text{ V}$,
$0.50 < t/T < 0.75\text{:}\hspace{0.4cm} r(t) = 0 \hspace{0.02cm}\text{ V}$,
$0.75 < t/T < 1.00\text{:}\hspace{0.4cm} r(t) = +2 \hspace{0.02cm}\text{ V}$.

The values we are looking for are thus

$$r(t = 0.2 \cdot T) \hspace{0.15cm}\underline{= +1 \hspace{0.02cm}\text{ V}},$$

$$r(t = 0.3 · T) \hspace{0.15cm}\underline{= -1 \hspace{0.02cm}\text{ V}}.$$

(3) Using a similar procedure as in (2), a direct signal $\rm (DC)$ of $2\hspace{0.02cm}\text{ V}$ is obtained for $r(t)$ :

The gaps in the signal $s(t)$ are completely filled by the echo $s(t - T/2)$.
This result can also be derived in the frequency domain. The channel frequency response is with $\alpha = 1$ and $\tau = T/2$:

$$H( f ) = 1 + 1 \cdot {\rm{e}}^{ - {\rm{j\pi }}fT} = 1 + \cos ( {{\rm{\pi }}fT} ) - {\rm{j}} \cdot {\rm{sin}}( {{\rm{\pi }}fT} ).$$

Apart from the DC component, the input signal ${s(t)}$ only has components at $f = f_0 = 1/T$, $f = 3 \cdot f_0$, $f = 5 \cdot f_0$, etc..
At these frequencies, however, both the real– and the imaginary part of ${H(f)}$ are equal to zero.
Thus, for the output spectrum with $A_0 = 1 \text{ V}$ and $H(f = 0) = 2$ we obtain:

$$R(f) = A_0 \cdot H(f = 0) \cdot \delta (f) = 2\;{\rm{V}} \cdot \delta (f).$$

The inverse Fourier transformation thus also yields $r(t) \underline{= 2 \text{ V= const}}$.