Exercise 4.11: C Program "acf1"

• Return to book

C program  $1$  for the ACF calculation

See the C–program "acf1" for calculating the discrete ACF values  $\varphi_x(k)$  with index  $k = 0$, ... , $l$.  The following should be noted about this:

• The long–value passed to the program is  $l = 10$.  The ACF values  $\varphi_x(0)$, ... , $\varphi_x(10)$  are returned to the calling program with the float field  $\rm ACF\big[ \ \big]$.  In lines 7 and 8 of the program given on the right,  this field is pre-populated with zeros.

• The random variables  $x_\nu$  to be analyzed are generated with the float function  $x( \ )$,  see line 4.  This function is called a total of  $N + l + 1 = 10011$  times  $x_\nu$  (lines 9 and 18).

• In contrast to the algorithm given in the  Theory section  directly implemented in the program  "acf2"  of  Task 4.11Z,  one needs here an auxiliary field  ${\rm H}\big[ \ \big]$  with only  $l + 1 = 11$  memory elements.

• Before starting the actual calculation algorithm (lines 11 to 21),  the eleven memory cells of  ${\rm H}\big[ \ \big]$  contain the random values  $x_1$, ... ,  $x_{11}$.  The outer loop with the index  $z$   (marked in red)  is run  $N$  times.
• In the inner loop   (marked white)  with the index  $k = 0$, ... ,  $l$  all memory cells of the field  ${\rm ACF}\big[\hspace{0.03cm} k \hspace{0.03cm} \big]$  are increased by the contribution  $x_\nu \cdot x_{\nu+k}$.

• Finally,  in lines 22 and 23,  all ACF values are divided by the number  $N$  of analyzed data.

Hint:

• This exercise belongs to the chapter  Auto-Correlation Function.
• Reference is made in particular to the page  Numerical ACF determination.

Questions

1

Which elements  $i$  and  $j$  of the auxiliary field  ${\rm H}\big[ \ \big]$  are used  on the first loop pass   $(z=0)$  to calculate the ACF–value  $\varphi(k=6)$ ?
What random values  $x_\nu$  are in these memory cells?

$i \ = \ $

$j \ = \ $

2

Which memory cell  ${\rm H}\big[\hspace{0.03cm} i \hspace{0.03cm} \big]$  will be occupied  after the first loop pass   $(z=0)$  with a new random variable  $x_\nu$ ?
Which index   $\nu$  is entered in the process?

$i \ = \ $

$\nu\ =\ $

3

Which memory elements  ${\rm H}\big[\hspace{0.03cm} i \hspace{0.03cm} \big]$  and  ${\rm H}\big[\hspace{0.03cm} j \hspace{0.03cm} \big]$  are used in the loop pass  $z=83$  to calculate the ACF value  $\varphi(k=6)$ ?
What random values are in these memory cells?

$i \ = \ $

$j \ = \ $

Solution

Solution

For the exemplary numerical ACF calculation

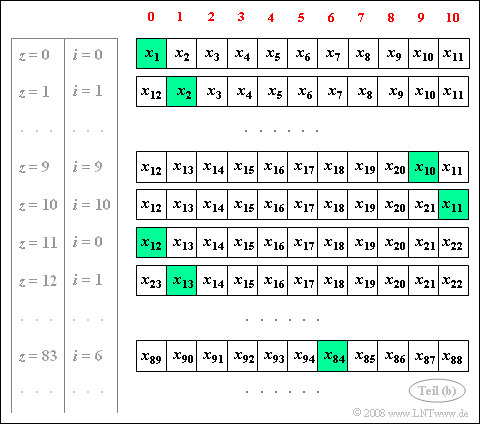
(1)  With  $z= 0$  and  $k=6$  results according to the program:   $\underline{i= 0}$  and  $\underline{j= 6}$.

• The corresponding memory contents are  ${\rm H}\big[\hspace{0.03cm} 0 \hspace{0.03cm}\big] = x_1$  and  ${\rm H}\big[\hspace{0.03cm} 6 \hspace{0.03cm}\big] = x_7$.

(2)  In the field  ${\rm H}\big[\hspace{0.03cm} 0 \hspace{0.03cm}\big]$  the random variable  $x_{12}$  is now entered:

$$\text{memory cell }\underline{i= 0},\hspace{1cm}\text{sequence index }\underline{\nu= 12}.$$

(3)  The graph shows the allocation of the auxiliary field with the random values  $x_\nu$.

• In each case,  the memory cell  ${\rm H}\big[\hspace{0.03cm} i \hspace{0.03cm}\big]$  is highlighted in green.  The new random variable is entered into this memory location at the end of each loop  (line 18).
• For  $z= 83$  and  $K=6$  this results in

$$\underline{i= 83 \hspace{-0.2cm}\mod \hspace{-0.15cm} \ 11 = 6},\hspace{1cm} \underline{j= (i+k)\hspace{-0.2cm}\mod \hspace{-0.15cm} \ 11 = 1}.$$

• Loop pass  $z= 83$:   In memory cell  ${\rm H}\big[\hspace{0.03cm} 6 \hspace{0.03cm}\big]$  is the random variable  $x_{84}$  and in the memory cell  ${\rm H}\big[\hspace{0.03cm} 1 \hspace{0.03cm}\big]$  is the random variable  $x_{90}$.
• At the end of loop pass  $z= 83$  in  ${\rm H}\big[\hspace{0.03cm} 6 \hspace{0.03cm}\big]$:  The content  $x_{84}$  is replaced by  $x_{95}$ .