Exercise 4.16: Eigenvalues and Eigenvectors

Three correlation matrices

Although the description of Gaussian random variables using vectors and matrices is actually only necessary and makes sense for more than $N = 2$ dimensions, here we restrict ourselves to the special case of two-dimensional random variables for simplicity.

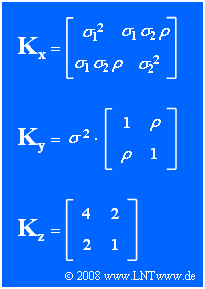
In the graph above, the general correlation matrix $\mathbf{K_x}$ of the two-dimensional random variable $\mathbf{x} = (x_1, x_2)^{\rm T}$ is given, where $\sigma_1^2$ and $\sigma_2^2$ describe the variances of the individual components. $\rho$ denotes the correlation coefficient between the two components.

The random variables $\mathbf{y}$ and $\mathbf{z}$ give two special cases of $\mathbf{x}$ whose process parameters are to be determined from the correlation matrices $\mathbf{K_y}$ and $\mathbf{K_z}$ respectively.

Hints:

The exercise belongs to the chapter Generalization to N-Dimensional Random Variables.
Some basics on the application of vectors and matrices can be found on the pages Determinant of a Matrix and Inverse of a Matrix .
According to the page "Contour lines for correlated random variables" the angle $\alpha$ between the old and the new system is given by the following equation:

$$\alpha = {1}/{2}\cdot \arctan (2 \cdot\rho \cdot \frac{\sigma_1\cdot\sigma_2}{\sigma_1^2 -\sigma_2^2}).$$

In particular, note:
- A $2×2$-covariance matrix has two real eigenvalues $\lambda_1$ and $\lambda_2$.
- These two eigenvalues determine two eigenvectors $\xi_1$ and $\xi_2$.
- These span a new coordinate system in the direction of the principal axes of the old system.

Questions

	$\mathbf{K_y}$ describes all possible two-dimensional random variables with $\sigma_1 = \sigma_2 = \sigma$.
	The value range of the parameter $\rho$ is $-1 \le \rho \le +1$.
	The value range of the parameter $\rho$ is $0 < \rho < 1$.

$\lambda_1 \ = \ $

$\ (\lambda_1 \ge \lambda_2)$

$\lambda_2 \ = \ $

$\ (\lambda_2 \le \lambda_1)$

$\lambda_1 \ = \ $

$\ (\lambda_1 \ge \lambda_2)$

$\lambda_2 \ = \ $

$\ (\lambda_2 \le \lambda_1)$

	$\mathbf{\eta_1}$ and $\mathbf{\eta_2}$ lie in the direction of the ellipse main axes.
	The new coordinates are rotated by $45^\circ$.
	The standard deviations with respect to the new system are $\lambda_1$ and $\lambda_2$.

$\sigma_1 = \ $

$\sigma_2 = \ $

$\rho = \ $

$\lambda_1 \ = \ $

$\ (\lambda_1 \ge \lambda_2)$

$\lambda_2 \ = \ $

$\ (\lambda_2 \le \lambda_1)$

$\alpha \ = \ $

$\ \rm deg$

Solution

(1) Correct are the proposed solutions 1 and 2:

$\mathbf{K_y}$ is indeed the most general correlation matrix of a two-dimensional random variable with $\sigma_1 = \sigma_2 = \sigma$.
The parameter $\rho$ specifies the correlation coefficient. This can take all values between $\pm 1$ including these marginal values.

(2) In this case, the governing equation is:

$${\rm det}\left[ \begin{array}{cc} 1- \lambda & 0 \\ 0 & 1- \lambda \end{array} \right] = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} (1- \lambda)^2 = 0\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \hspace{0.15cm}\underline{\lambda_{1/2} =1}.$$

(3) With positive $\rho$ the governing equation of the eigenvalues is:

$$(1- \lambda)^2 -\rho^2 = 0\hspace{0.5cm}\Rightarrow \hspace{0.5cm}\lambda^2 - 2\lambda + 1 - \rho^2 = 0\hspace{0.5cm}\Rightarrow\hspace{0.5cm}\lambda_{1/2} =1 \pm \rho.$$

For $\rho= 0.5$ one gets $\underline{\lambda_{1} =1.5}$ and $\underline{\lambda_{2} =0.5}$.
By the way, the equation holds in the whole domain of definition $-1 \le \rho \le +1$.
For $\rho = 0$ ⇒ $\lambda_1 = \lambda_2 = +1$ ⇒ see subtask (2).
For $\rho = \pm 1$ ⇒ $\lambda_1 = 2$ and $\lambda_2 = 0$.

(4) Correct are the proposed solutions 1 and 2.

The eigenvectors are obtained by substituting the eigenvalues $\lambda_1$ and $\lambda_2$ into the correlation matrix:

$$\left[ \begin{array}{cc} 1- (1+\rho) & \rho \\ \rho & 1- (1+\rho) \end{array} \right]\cdot{\boldsymbol{\eta_1}} = \left[ \begin{array}{cc} -\rho & \rho \\ \rho & -\rho \end{array} \right]\cdot \left[ \begin{array}{c} \eta_{11} \\ \eta_{12} \end{array} \right]=0$$

$$\Rightarrow\hspace{0.3cm}-\rho \cdot \eta_{11} + \rho \cdot \eta_{12} = 0\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\eta_{11}= {\rm const} \cdot \eta_{12}\hspace{0.3cm}\Rightarrow\hspace{0.3cm}{\boldsymbol{\eta_1}}= {\rm const}\cdot \left[ \begin{array}{c} 1 \\ 1 \end{array} \right];$$

$$\left[ \begin{array}{cc} 1- (1-\rho) & \rho \\ \rho & 1- (1-\rho) \end{array} \right]\cdot{\boldsymbol{\eta_2}} = \left[ \begin{array}{cc} \rho & \rho \\ \rho & \rho \end{array} \right]\cdot \left[ \begin{array}{c} \eta_{21} \\ \eta_{22} \end{array} \right]=0$$

$$\Rightarrow\hspace{0.3cm}\rho \cdot \eta_{21} + \rho \cdot \eta_{22} = 0\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\eta_{21}= -{\rm const} \cdot \eta_{22}\hspace{0.3cm}\Rightarrow\hspace{0.3cm}{\boldsymbol{\eta_2}}= {\rm const}\cdot \left[ \begin{array}{c} -1 \\ 1 \end{array} \right].$$

Rotate the coordinate system

Putting this into the "orthonormal form", the following holds:

$${\boldsymbol{\eta_1}}= \frac{1}{\sqrt{2}}\cdot \left[ \begin{array}{c} 1 \\ 1 \end{array} \right],\hspace{0.5cm} {\boldsymbol{\eta_2}}= \frac{1}{\sqrt{2}}\cdot \left[ \begin{array}{c} -1 \\ 1 \end{array} \right].$$

The sketch illustrates the result:

The coordinate system defined by $\mathbf{\eta_1}$ and $\mathbf{\eta_2}$ is actually in the direction of the main axes of the original system.
With $\sigma_1 = \sigma_2$ almost always results $($exception: $\rho= 0)$ the rotation angle $\alpha = 45^\circ$.
This also follows from the equation given in the theory section:

$$\alpha = {1}/{2}\cdot \arctan (2 \cdot\rho \cdot \frac{\sigma_1\cdot\sigma_2}{\sigma_1^2 -\sigma_2^2})= {1}/{2}\cdot \arctan (\infty)\hspace{0.3cm}\rightarrow\hspace{0.3cm}\alpha = 45^\circ.$$

The eigenvalues $\lambda_1$ and $\lambda_2$ do not denote the standard deviations with respect to the new axes, but the variances.

(5) By comparing the matrices $\mathbf{K_x}$ and $\mathbf{K_z}$ we get.

$\sigma_{1}\hspace{0.15cm}\underline{ =2}$,
$\sigma_{2}\hspace{0.15cm}\underline{ =1}$,
$\rho = 2/(\sigma_{1} \cdot \sigma_{2})\hspace{0.15cm}\underline{ =1}$.

(6) According to the now familiar scheme:

$$(4- \lambda) \cdot (1- \lambda) -4 = 0\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\lambda^2 - 5\lambda = 0\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\hspace{0.15cm}\underline{\lambda_{1} =5,\hspace{0.1cm} \lambda_{2} =0}.$$

(7) According to the equation given on the specification sheet:

$$\alpha ={1}/{2}\cdot \arctan (2 \cdot 1 \cdot \frac{2 \cdot 1}{2^2 -1^2})= {1}/{2}\cdot \arctan ({4}/{3}) = 26.56^\circ.$$

Best possible decorrelation

The same result is obtained using the eigenvector:

$$\left[ \begin{array}{cc} 4-5 & 2 \\ 2 & 1-5 \end{array} \right]\cdot \left[ \begin{array}{c} \zeta_{11} \\ \zeta_{12} \end{array} \right]=0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}-\zeta_{11}= 2\zeta_{12}=0\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\zeta_{12}={\zeta_{11}}/{2}$$

$$\Rightarrow\hspace{0.3cm}\alpha = \arctan ({\zeta_{12}}/{\zeta_{11}}) = \arctan(0.5) \hspace{0.15cm}\underline{= 26.56^\circ}.$$

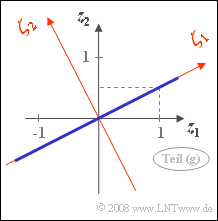
The accompanying sketch shows the joint PDF of the random variable $\mathbf{z}$:

Because of $\rho = 1$ all values lie on the correlation line with coordinates $z_1$ and $z_2 = z_1/2$.
By rotating by the angle $\alpha = \arctan(0.5) = 26.56^\circ$ a new coordinate system is formed.
The variance along the axis $\mathbf{\zeta_1}$ is $\lambda_1 = 5$ $($standard deviation $\sigma_1 = \sqrt{5} = 2.236)$,
while in the direction orthogonal to it, the random variable $\mathbf{\zeta_2}$ is not extended $(\lambda_2 = \sigma_2 = 0)$.