Exercise 4.4: Extrinsic L-values at SPC

• Return to book

Suitable auxiliary table

We consider again the  "single parity–check code".  In such a  ${\rm SPC} \ (n, \, n-1, \, 2)$  the  $n$  bits of a code word  $\underline{x}$  come from the  $k = n -1$  bits from the source sequence  $\underline{u}$  and only a single check bit  $p$  is added,  such that the number of  "ones"  in the code word  $\underline{x}$  is even:

$$\underline{x} = \big ( \hspace{0.03cm}x_1, \hspace{0.03cm} x_2, \hspace{0.05cm} \text{...} \hspace{0.05cm} , x_{n-1}, \hspace{0.03cm} x_n \hspace{0.03cm} \big ) = \big ( \hspace{0.03cm}u_1, \hspace{0.03cm} u_2, \hspace{0.05cm} \text{...} \hspace{0.05cm} , u_{k}, \hspace{0.03cm} p \hspace{0.03cm} \big )\hspace{0.03cm}.$$

The extrinsic information about the  $i$th code bit is formed over all other bits  $(j ≠ i)$.  Therefore we write for the code word shorter by one bit:

$$\underline{x}^{(-i)} = \big ( \hspace{0.03cm}x_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \hspace{0.03cm} x_{i-1}, \hspace{0.43cm} x_{i+1}, \hspace{0.05cm} \text{...} \hspace{0.05cm} , x_{n} \hspace{0.03cm} \big )\hspace{0.03cm}.$$

The extrinsic  L–value over the  $i$th code symbol reads with the  "Hamming weight"  $w_{\rm H}$  of the truncated sequence  $\underline{x}^{(-i)}$:

$$L_{\rm E}(i) = \frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} even} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} \hspace{0.05cm}.$$

• If the probability in the numerator is greater than that in the denominator,  then  $L_{\rm E}(i) > 0$  and thus the a-posteriori L–value  $L_{\rm APP}(i) = L_{\rm A}(i) + L_{\rm E}(i)$  magnified,  that is tends to be affected in the direction of the symbol  $x_i = 0$.

• If  $L_{\rm E}(i) < 0$  then there is much to be said for  $x_i = 1$  from the point of view of the other symbols  $(j ≠ i)$.

Only the  $\text{SPC (4, 3, 4)}$  is treated,  where for the probabilities  $p_i = {\rm Pr}(x_i = 1)$  holds:

$$p_1 = 0.2 \hspace{0.05cm}, \hspace{0.3cm} p_2 = 0.9 \hspace{0.05cm}, \hspace{0.3cm} p_3 = 0.3 \hspace{0.05cm}, \hspace{0.3cm} p_4 = 0.6 \hspace{0.05cm}.$$

From this the a-priori log likelihood ratios result to:

$$L_{\rm A}(i) = {\rm ln} \hspace{0.1cm} \left [ \frac{{\rm Pr}(x_i = 0)}{{\rm Pr}(x_i = 1)} \right ] = {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_i}{p_i} \right ] \hspace{0.05cm}.$$

Hints:

• This exercise belongs to the chapter  "Soft–in Soft–out Decoder".

• Reference is made in particular to the section  "Calculation of the extrinsic log likelihood ratios".

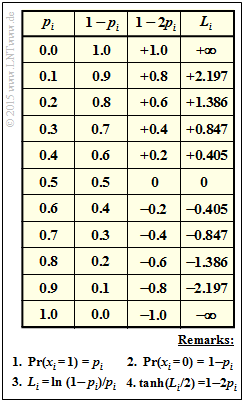
• In the table are given for  $p_i = 0$  to  $p_i = 1$  with step size  $0.1$  $($column 1$)$:

In column 2:   the probability  $q_i = {\rm Pr}(x_i = 0) = 1 - p_i$,

in column 3:   the values for  $1 - 2p_i$,

in column 4:   the a-priori log likelihood ratios  $L_i = \ln {\big [(1 - p_i)/p_ i \big ]} = L_{\rm A}(i)$.

• The  "hyperbolic tangent"  $(\tanh)$  of $L_i/2$  is identical to  $1-2p_i$   ⇒   column 3.

• In  $\text{Exercise 4.4Z}$  it is shown that for the extrinsic  L–value can also be written:

$$L_{\rm E}(i) = {\rm ln} \hspace{0.2cm} \frac{1 + \pi}{1 - \pi}\hspace{0.05cm}, \hspace{0.3cm} {\rm mit} \hspace{0.3cm} \pi = \prod\limits_{j \ne i}^{n} \hspace{0.25cm}(1-2p_j) \hspace{0.05cm}.$$

Questions

1

It holds  $p_1 = 0.2, \ p_2 = 0.9, \ p_3 = 0.3, \ p_4 = 0.6$.  From this,  calculate the a-priori log likelihood ratios of the  $\text{SPC (4, 3, 4)}$  for bit 1 and bit 2.

$L_{\rm A}(i = 1) \ = \ $

$L_{\rm A}(i = 2) \ = \ $

2

What are the extrinsic log likelihood ratios for bit 1 and bit 2.

$L_{\rm E}(i = 1) \ = \ $

$L_{\rm E}(i = 2) \ = \ $

3

What are the relationships between  $p_j$  and  $L_j = L_{\rm A}(j)$?

	It holds  $p_j = 1/(1 + {\rm e}^ {L_j})$.
	It holds  $1-2p_j = ({\rm e}^ {L_j} - 1) \ / \ ({\rm e}^ {L_j} + 1)$.
	It holds  $1-2p_j = \tanh {(L_j/2)}$.

4

It is further  $p_1 = 0.2, \ p_2 = 0.9, \ p_3, \ p_4 = 0.6$.  Calculate the extrinsic log likelihood ratios for bit 3 and bit 4.  Use different equations for this purpose.

$L_{\rm E}(i = 3) \ = \ $

$L_{\rm E}(i = 4) \ = \ $

Solution

Solution

(1)  For the a-priori log likelihood ratios of the first two bits of the code word:

$$L_{\rm A}(i = 1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_1}{p_1} \right ] = {\rm ln} \hspace{0.1cm} 4 \hspace{0.15cm}\underline{= +1.386} \hspace{0.05cm},$$

$$L_{\rm A}(i = 2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_2}{p_2} \right ] = {\rm ln} \hspace{0.1cm} 1/9 \hspace{0.15cm}\underline{= -2.197} \hspace{0.05cm}.$$

• The values can be read from the fourth column of the table attached to the information page.

(2)  To calculate the extrinsic L–value over the  $i$th bit,  only the information about the other three bits  $(j ≠ i)$  may be used.  With the given equation holds:

$$L_{\rm E}(i = 1) = {\rm ln} \hspace{0.2cm} \frac{1 + \prod\limits_{j \ne 1} \hspace{0.25cm}(1-2p_j)}{1 - \prod\limits_{j \ne 1} \hspace{0.25cm}(1-2p_j)} \hspace{0.05cm}.$$

• For the product,  we obtain according to the third column of the  $\rm table$:

$$\prod\limits_{j =2, \hspace{0.05cm}3,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = (-0.8) \cdot (+0.4) \cdot (-0.2) = 0.064 \hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}L_{\rm E}(i = 1) = {\rm ln} \hspace{0.2cm} \frac{1 + 0.064}{1 - 0.064} = {\rm ln} \hspace{0.1cm} (1.137)\hspace{0.15cm}\underline{= +0.128} \hspace{0.05cm}.$$

• In terms of bit 2,  one obtains accordingly:

$$\prod\limits_{j =1, \hspace{0.05cm}3,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = (+0.6) \cdot (+0.4) \cdot (-0.2) = -0.048 \hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}L_{\rm E}(i = 2) = {\rm ln} \hspace{0.2cm} \frac{1 -0.048}{1 +0.048} = {\rm ln} \hspace{0.1cm} (0.908)\hspace{0.15cm}\underline{= -0.096} \hspace{0.05cm}.$$

(3)  For the a-priori L– value holds:

$$L_j = L_{\rm A}(j) = {\rm ln} \hspace{0.1cm} \left [ \frac{{\rm Pr}(x_j = 0)}{{\rm Pr}(x_j = 1)} \right ] = {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_j}{p_j} \right ]\hspace{0.3cm} \Rightarrow \hspace{0.3cm} 1-p_j = p_j \cdot {\rm e}^{L_j} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_j = \frac{1}{1+{\rm e}^{L_j} } \hspace{0.05cm} .$$

• Thus also applies:

$$1- 2 \cdot p_j = 1 - \frac{2}{1+{\rm e}^{L_j} } = \frac{1+{\rm e}^{L_j}-2}{1+{\rm e}^{L_j} } = \frac{{\rm e}^{L_j}-1}{{\rm e}^{L_j} +1}\hspace{0.05cm} .$$

• Multiplying the numerator and denominator by  ${\rm e}^{-L_j/2}$,  we get:

$$1- 2 \cdot p_j = \frac{{\rm e}^{L_j/2}-{\rm e}^{-L_j/2}}{{\rm e}^{L_j/2}+{\rm e}^{-L_j/2}}={\rm tanh} (L_j/2) \hspace{0.05cm} .$$

• Thus  all proposed solutions are correct.

• The function  "hyperbolic tangent"  can be found,  for example,  in tabular form in formula collections or in the last column of the table given in front.

(4)  We first calculate  $L_{\rm E}(i = 3)$  in the same way as in subtask  (2):

$$\prod\limits_{j =1, \hspace{0.05cm}2,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = (+0.6) \cdot (-0.8) \cdot (-0.2) = +0.096 \hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}L_{\rm E}(i = 3) = {\rm ln} \hspace{0.2cm} \frac{1 +0.096}{1 -0.096} = {\rm ln} \hspace{0.1cm} (1.212)\hspace{0.15cm}\underline{= +0.193} \hspace{0.05cm}.$$

• We calculate the extrinsic L–value with respect to the last bit according to the equation

$$L_{\rm E}(i = 4) = {\rm ln} \hspace{0.2cm} \frac{1 + \pi}{1 - \pi}\hspace{0.05cm}, \hspace{0.3cm} {\rm with} \hspace{0.3cm} \pi = {\rm tanh}(L_1/2) \cdot {\rm tanh}(L_2/2) \cdot {\rm tanh}(L_3/2) \hspace{0.05cm}.$$

• This results in accordance with the above  $\rm table$:

$$p_1 = 0.2 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_1 = +1.386 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_1/2 = +0.693 \hspace{0.2cm} \Rightarrow \hspace{0.2cm} {\rm tanh}(L_1/2) = \frac{{\rm e}^{+0.693}-{\rm e}^{-0.693}}{{\rm e}^{+0.693}+{\rm e}^{-0.693}} = 0.6 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm identisch \hspace{0.15cm}mit\hspace{0.15cm} }1-2\cdot p_1\hspace{0.05cm},$$

$$p_2 = 0.9 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_2 = -2.197 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_2/2 = -1.099\hspace{0.2cm} \Rightarrow \hspace{0.2cm} {\rm tanh}(L_2/2) = \frac{{\rm e}^{-1.099}-{\rm e}^{+1.099}}{{\rm e}^{-1.099}+{\rm e}^{+1.099}} = -0.8 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm identisch \hspace{0.15cm}mit\hspace{0.15cm} }1-2\cdot p_2\hspace{0.05cm},$$

$$p_3 = 0.3 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_3 = 0.847 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_3/2 = +0.419 \hspace{0.2cm} \Rightarrow \hspace{0.2cm} {\rm tanh}(L_3/2) = \frac{{\rm e}^{+0.419}-{\rm e}^{-0.419}}{{\rm e}^{+0.419}+{\rm e}^{-0.419}} = 0.4 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm identisch \hspace{0.15cm}mit\hspace{0.15cm} }1-2\cdot p_3\hspace{0.05cm}.$$

• The final result is thus:

$$\pi = (+0.6) \cdot (-0.8) \cdot (+0.4) = -0.192 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} L_{\rm E}(i = 4) = {\rm ln} \hspace{0.2cm} \frac{1 -0.192}{1 +0.192}\hspace{0.15cm}\underline{= -0.389} \hspace{0.05cm}.$$