Difference between revisions of "Applets:Diskrete Fouriertransformation und Inverse"
| Line 19: | Line 19: | ||
==Theoretischer Hintergrund== | ==Theoretischer Hintergrund== | ||
<br> | <br> | ||
| − | === | + | ===Diskrete Fouriertransformation=== |
| − | + | Aus dem herkömmlichen „ersten Fourierintegral” | |
| + | |||
| + | :$$X(f) =\int_{-\infty | ||
| + | }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}t$$ | ||
| − | + | entsteht durch Diskretisierung $(\text{d}t \to T_{\rm A}$, $t \to \nu \cdot T_{\rm A}$, $f \to \mu \cdot f_{\rm A}$, $T_{\rm A} \cdot f_{\rm A} = 1/N)$ die abgetastete und periodifizierte Spektralfunktion | |
| − | $\text{ | + | |
| − | + | :$${\rm P}\{X(\mu \cdot f_{\rm A})\} = T_{\rm A} \cdot \sum_{\nu = 0 }^{N-1} | |
| − | :$$ | + | {\rm P}\{x(\nu \cdot T_{\rm A})\}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm} \cdot \hspace{0.05cm}\nu \hspace{0.05cm} |
| + | \cdot \hspace{0.05cm}\mu /N} \hspace{0.05cm}.$$ | ||
| − | + | Es ist berücksichtigt, dass aufgrund der Diskretisierung jeweils die periodifizierten Funktionen einzusetzen sind. | |
| − | |||
| − | |||
| − | |||
| + | Aus Gründen einer vereinfachten Schreibweise nehmen wir nun die folgenden Substitutionen vor: | ||
| + | *Die $N$ '''Zeitbereichskoeffizienten''' seien mit der Laufvariablen $\nu = 0$, ... , $N - 1$: | ||
| + | :$$d(\nu) = | ||
| + | {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.05cm}.$$ | ||
| + | *Die $N$ '''Frequenzbereichskoeffizienten''' seien mit der Laufvariablen $\mu = 0,$ ... , $N$ – 1: | ||
| + | :$$D(\mu) = f_{\rm A} \cdot | ||
| + | {\rm P}\left\{X(f)\right\}{\big|}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A}}\hspace{0.05cm}.$$ | ||
| + | *Abkürzend wird für den von $N$ abhängigen '''komplexen Drehfaktor''' geschrieben: | ||
| + | :$$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} | ||
| + | = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) | ||
| + | \hspace{0.05cm}.$$ | ||
| − | + | [[File:P_ID2730__Sig_T_5_1_S5_neu.png|right|frame|Zur Definition der Diskreten Fouriertransformation (DFT) mit $N=8$]] | |
| − | + | {{BlaueBox|TEXT= | |
| − | + | $\text{Definition:}$ | |
| − | + | Unter dem Begriff '''Diskrete Fouriertransformation''' (kurz '''DFT''') versteht man die Berechnung der $N$ Spektralkoeffizienten $D(\mu)$ aus den $N$ Signalkoeffizienten $d(\nu)$: | |
| − | + | ||
| − | + | :$$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} | |
| + | d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}. $$ | ||
| + | In der Grafik erkennt man an einem Beispiel | ||
| + | *die $N = 8$ Signalkoeffizienten $d(\nu)$ an der blauen Füllung, | ||
| + | *die $N = 8$ Spektralkoeffizienten $D(\mu)$ an der grünen Füllung.}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ===Inverse Diskrete Fouriertransformation=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Die Inverse Diskrete Fouriertransformation (IDFT) beschreibt das „zweite Fourierintegral” | |
| + | |||
| + | :$$\begin{align*}x(t) & = \int_{-\infty | ||
| + | }^{+\infty}X(f) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm} | ||
| + | t}\hspace{0.1cm} {\rm d}f\end{align*}$$ | ||
| − | + | in diskretisierter Form: $d(\nu) = | |
| − | + | {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm | |
| − | + | A}}\hspace{0.01cm}.$ | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | {{BlaueBox|TEXT= | + | [[File:P_ID2731__Sig_T_5_1_S6_neu.png|right|frame|Zur Definition der IDFT mit $N=8$]] |
| − | $\text{ | + | {{BlaueBox|TEXT= |
| − | + | $\text{Definition:}$ | |
| − | + | Unter dem Begriff '''Inverse Diskrete Fouriertransformation''' (kurz '''IDFT''') versteht man die Berechnung der Signalkoeffizienten $d(\nu)$ aus den Spektralkoeffizienten $D(\mu)$: | |
| − | + | ||
| − | + | :$$d(\nu) = \sum_{\mu = 0 }^{N-1} | |
| − | + | D(\mu) \cdot {w}^{-\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$ | |
| − | |||
| − | |||
| − | + | Mit den Laufvariablen $\nu = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, N-1$ und $\mu = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, N-1$ gilt auch hier: | |
| − | + | :$$d(\nu) = | |
| + | {\rm P}\left\{x(t)\right\}{\big \vert}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm | ||
| + | A} }\hspace{0.01cm},$$ | ||
| + | |||
| + | :$$D(\mu) = f_{\rm A} \cdot | ||
| + | {\rm P}\left\{X(f)\right\}{\big \vert}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A} } | ||
| + | \hspace{0.01cm},$$ | ||
| − | + | :$$w = {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} | |
| + | \hspace{0.01cm}.$$}} | ||
| − | + | ||
| − | Die | + | Ein Vergleich zwischen DFT und IDFT zeigt, dass genau der gleiche Algorithmus verwendet werden kann. Die einzigen Unterschiede der IDFT gegenüber der DFT sind: |
| − | * | + | *Der Exponent des Drehfaktors ist mit unterschiedlichem Vorzeichen anzusetzen. |
| − | * | + | *Bei der IDFT entfällt die Division durch $N$. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br><br> | <br><br> | ||
Revision as of 14:32, 2 September 2019
!!! Diese App wird gerade entwickelt. Entwicklungsstufe 0. Hat mit dem angekündigten Thema noch nichts zu tun!!!
Contents
Programmbeschreibung
Das Applet verdeutlicht die Eigenschaften zweidimensionaler Gaußscher Zufallsgrößen $XY\hspace{-0.1cm}$, gekennzeichnet durch die Standardabweichungen (Streuungen) $\sigma_X$ und $\sigma_Y$ ihrer beiden Komponenten sowie den Korrelationskoeffizienten $\rho_{XY}$ zwischen diesen. Die Komponenten werden als mittelwertfrei vorausgesetzt: $m_X = m_Y = 0$.
Das Applet zeigt
- die zweidimensionale Wahrscheinlichkeitsdichtefunktion ⇒ $\rm 2D\hspace{-0.1cm}-\hspace{-0.1cm}WDF$ $f_{XY}(x, \hspace{0.1cm}y)$ in dreidimensionaler Darstellung sowie in Form von Höhenlinien,
- die zugehörige Randwahrscheinlichkeitsdichtefunktion ⇒ $\rm 1D\hspace{-0.1cm}-\hspace{-0.1cm}WDF$ $f_{X}(x)$ der Zufallsgröße $X$ als blaue Kurve; ebenso $f_{Y}(y)$ für die zweite Zufallsgröße,
- die zweidimensionale Verteilungsfunktion ⇒ $\rm 2D\hspace{-0.1cm}-\hspace{-0.1cm}VTF$ $F_{XY}(x, \hspace{0.1cm}y)$ als 3D-Plot,
- die Verteilungsfunktion ⇒ $\rm 1D\hspace{-0.1cm}-\hspace{-0.1cm}VTF$ $F_{X}(x)$ der Zufallsgröße $X$; ebenso $F_{Y}(y)$ als rote Kurve.
Das Applet verwendet das Framework Plot.ly
Theoretischer Hintergrund
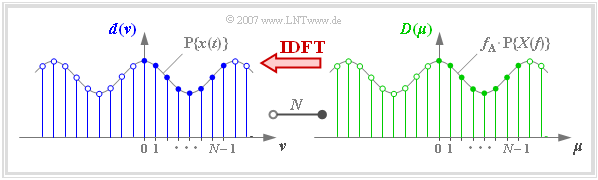
Diskrete Fouriertransformation
Aus dem herkömmlichen „ersten Fourierintegral”
- $$X(f) =\int_{-\infty }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}t$$
entsteht durch Diskretisierung $(\text{d}t \to T_{\rm A}$, $t \to \nu \cdot T_{\rm A}$, $f \to \mu \cdot f_{\rm A}$, $T_{\rm A} \cdot f_{\rm A} = 1/N)$ die abgetastete und periodifizierte Spektralfunktion
- $${\rm P}\{X(\mu \cdot f_{\rm A})\} = T_{\rm A} \cdot \sum_{\nu = 0 }^{N-1} {\rm P}\{x(\nu \cdot T_{\rm A})\}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm} \cdot \hspace{0.05cm}\nu \hspace{0.05cm} \cdot \hspace{0.05cm}\mu /N} \hspace{0.05cm}.$$
Es ist berücksichtigt, dass aufgrund der Diskretisierung jeweils die periodifizierten Funktionen einzusetzen sind.
Aus Gründen einer vereinfachten Schreibweise nehmen wir nun die folgenden Substitutionen vor:
- Die $N$ Zeitbereichskoeffizienten seien mit der Laufvariablen $\nu = 0$, ... , $N - 1$:
- $$d(\nu) = {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.05cm}.$$
- Die $N$ Frequenzbereichskoeffizienten seien mit der Laufvariablen $\mu = 0,$ ... , $N$ – 1:
- $$D(\mu) = f_{\rm A} \cdot {\rm P}\left\{X(f)\right\}{\big|}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A}}\hspace{0.05cm}.$$
- Abkürzend wird für den von $N$ abhängigen komplexen Drehfaktor geschrieben:
- $$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) \hspace{0.05cm}.$$
$\text{Definition:}$
Unter dem Begriff Diskrete Fouriertransformation (kurz DFT) versteht man die Berechnung der $N$ Spektralkoeffizienten $D(\mu)$ aus den $N$ Signalkoeffizienten $d(\nu)$:
- $$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}. $$
In der Grafik erkennt man an einem Beispiel
- die $N = 8$ Signalkoeffizienten $d(\nu)$ an der blauen Füllung,
- die $N = 8$ Spektralkoeffizienten $D(\mu)$ an der grünen Füllung.
Inverse Diskrete Fouriertransformation
Die Inverse Diskrete Fouriertransformation (IDFT) beschreibt das „zweite Fourierintegral”
- $$\begin{align*}x(t) & = \int_{-\infty }^{+\infty}X(f) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm} t}\hspace{0.1cm} {\rm d}f\end{align*}$$
in diskretisierter Form: $d(\nu) = {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.01cm}.$
$\text{Definition:}$
Unter dem Begriff Inverse Diskrete Fouriertransformation (kurz IDFT) versteht man die Berechnung der Signalkoeffizienten $d(\nu)$ aus den Spektralkoeffizienten $D(\mu)$:
- $$d(\nu) = \sum_{\mu = 0 }^{N-1} D(\mu) \cdot {w}^{-\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$
Mit den Laufvariablen $\nu = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, N-1$ und $\mu = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, N-1$ gilt auch hier:
- $$d(\nu) = {\rm P}\left\{x(t)\right\}{\big \vert}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A} }\hspace{0.01cm},$$
- $$D(\mu) = f_{\rm A} \cdot {\rm P}\left\{X(f)\right\}{\big \vert}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A} } \hspace{0.01cm},$$
- $$w = {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} \hspace{0.01cm}.$$
Ein Vergleich zwischen DFT und IDFT zeigt, dass genau der gleiche Algorithmus verwendet werden kann. Die einzigen Unterschiede der IDFT gegenüber der DFT sind:
- Der Exponent des Drehfaktors ist mit unterschiedlichem Vorzeichen anzusetzen.
- Bei der IDFT entfällt die Division durch $N$.
Versuchsdurchführung
- Wählen Sie zunächst die Nummer (1, ...) der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von „Musterlösung”.
- Bei der Aufgabenbeschreibung verwenden wir $\rho$ anstelle von $\rho_{XY}$.
- Für die „1D-WDF” gilt: $f_{X}(x) = \sqrt{1/(2\pi \cdot \sigma_X^2)} \cdot {\rm e}^{-x^2/(2 \hspace{0.05cm}\cdot \hspace{0.05cm} \sigma_X^2)}$.
Die Nummer 0 entspricht einem „Reset”:
- Gleiche Einstellung wie beim Programmstart.
- Ausgabe eines „Reset–Textes” mit weiteren Erläuterungen zum Applet.
(1) Neue Einstellung: $\text{DFT von Signal (a): Gleichsignal}$. Interpretieren Sie das Ergebnis im Frequenzbereich. Wie lautet das Analogon der herkömmlichen FT?
- Im Zeitbereich sind alle $d(\nu) =1$. Dann sind alle $D(\mu) =0$ mit Ausnahme von ${\rm Re}\big [D(0)] =1$.
- Dies entspricht bei der herkömmlichen (zeitkontinuierlichen) Fouriertransformation: $x(t) = A\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = A \cdot \delta(f=0)$ mit $A=1$.
(2) Gehen Sie vom erhaltenen $D(\mu)$–Feld aus und verschieben Sie alle Koeffizienten um eine Stelle nach unten. Welche Zeitfunktion liefert die $\rm IDFT$?
- Nun sind alle $D(\mu) =0$ mit Ausnahme von ${\rm Re}\big [D(1)] =1$. Das Zeitbereichsergebnis ist eine komplexe Exonentialfunktion.
- Der Realteil des $d(\nu)$–Feldes zeigt einen Cosinus und der Imaginärteil eine Sinusfunktion. Bei beiden Funktionen erkennt man jeweils eine Periode.
(3) Ergänzen Sie das aktuelle $D(\mu)$–Feld um den Koeffizienten ${\rm Im}\big [D(1)] =1$. Welche Unterschiede erkennt man gegenüber (2) im Zeitbereich?
- Zum einen erkennt man nun bei Realteil und Imaginärteil eine Phasenverschiebung um zwei Stützwerte. Dies entspricht der Phase $\varphi = 45^\circ$.
- Zudem wurden die Amplituden von Real– und Imaginärteil jeweils um den Faktor $\sqrt{2}$ vergrößert.
(4) Setzen Sie das $D(\mu)$–Feld auf Null mit Ausnahme von ${\rm Re}\big [D(1)] =1$. Durch welchen zusätzlichen $D(\mu)$–Koeffizienten erhält man ein reelles $d(\nu)$–Feld?
- Durch Probieren oder Nachdenken erkennt man, dass auch ${\rm Re}\big [D(15)] =1$ gesetzt werden muss. Dann beschreibt das $d(\nu)$–Feld einen Cosinus.
- Für die herkömmliche (zeitkontinuierliche) Fouriertransformation gilt: $x(t) = 2 \cdot \cos(2\pi \cdot f_0 \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = \delta(f -f_0)+\delta(f +f_0)$.
- Das Feld $D(1)$ steht für die Frequenz $f_0$ und aufgrund der Periodizät mit $N=16$ wird die Frequenz $-f_0$ durch $D(15) = D(-1)$ ausgedrückt.
(5) Mit welchem $D(\mu)$–Feld erhält man nach der $\rm IDFT$ im $d(\nu)$–Feld eine reelle Cosinusfunktion mit der Amplitude $A=1$?
- Die Diskrete Fouriertransformation ist ebenso wie die herkömmliche Fouriertransformation linear ⇒ $D(1) = D(15)=0.5$.
(6) Neue Einstellung: $\text{DFT von Signal (e): Cosinussignal}$ und anschließende Signalverschiebungen. Was bewirken diese Verschiebungen im Frequenzbereich?
- Eine Verschiebung im Zeitbereich verändert das Cosinussignal zu einer „Harmonischen Schwingung” mit beliebiger Phase.
- Das $D(\mu)$–Feld ist weiterhin Null bis auf $D(1)$ und $D(15)$. Die Beträge $|D(1)|$ und $|D(15)|$ bleiben ebenfalls gleich.
- Die alleinige Veränderung betrifft die Phase, also die unterschiedliche Aufteilung der Beträge auf Real– und Imaginärteil.
(7) Neue Einstellung: $\text{DFT von Signal (f): Sinussignal}$. Interpretieren Sie das Ergebnis im Frequenzbereich. Wie lautet das Analogon der herkömmlichen FT?
- Das Sinussignal ergibt sich aus dem Cosinussignal durch vier Zeitverschiebungen. Deshalb gelten alle Aussagen von (6) weiterhin.
- Für die herkömmliche (zeitkontinuierliche) Fouriertransformation gilt: $x(t) = \sin(2\pi \cdot f_0 \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = {\rm j}/2 \cdot \big [\delta(f +f_0)-\delta(f -f_0)\big ]$.
- Der Koeffizient $D(1)$ ⇒ $($Frequenz: $+f_0)$ ist imaginär und hat den Imaginärteil $-0.5$. Entsprechend gilt ${\rm Im}\big [D(15)] =+0.5$ ⇒ $($Frequenz: $-f_0)$.
(8) Neue Einstellung: $\text{DFT von Signal (g): Cosinussignal (zwei Perioden)}$. Interpretieren Sie das Ergebnis im Vergleich zur Aufgabe (5).
- Hier lautet die zeitkontinuierliche Fouriertransformation: $x(t) = \cos(2\pi \cdot (2f_0) \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = 0.5 \cdot \delta(f -2 f_0)+0.5 \cdot \delta(f +2f_0)$.
- Für die Frequenz $2f_0$ steht das Feld $D(2)$ und für die Frequenz $-2f_0$ aufgrund der Periodizät das Feld $D(14) = D(-2)$ : $D(2) = D(14) = 0.5$.
(9) Untersuchen Sie nun den Fall $\text{DFT von Sinussignal (zwei Perioden)}$. Welche Einstellung müssen Sie vornehmen? Interpretieren Sie das Ergebnis.
- Zum gewünschten Signal kommt man von $\text{DFT von Signal (g): Cosinussignal (zwei Perioden)}$ mit zwei Verschiebungen. Bei (7): Vier Verschiebungen.
- Das DFT–Ergebnis lautet dementsprechend: ${\rm Im}\big [D(2)] =-0.5$ und ${\rm Im}\big [D(14)] =+0.5$.
(10) Neue Einstellung: $\text{DFT von (h) Alternierende Zeitkoeffizienten}$. Interpretieren Sie das DFT–Ergebnis.
- Hier lautet die zeitkontinuierliche Fouriertransformation: $x(t) = \cos(2\pi \cdot (8f_0) \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = 0.5 \cdot \delta(f -8 f_0)+0.5 \cdot \delta(f +8f_0)$.
- $8f_0$ ist die höchste mit $N=16$ in der DFT darstellbare Frequenz. Pro Periodendauer gibt es nur zwei Abtastwerte, nämlich $+1$ und $-1$.
- Unterschied zur Teilaufgabe (5): Aus $D(1) =0.5$ wird nun $D(8) =0.5$. Ebenso verschiebt sich $D(15) =0.5$ auf $D(8) =0.5$. Endergebnis: $D(8) =1$.
(11) Welche Unterschiede erhält man mit den beiden Einstellungen $\text{IDFT von Spektrum (C)}$ sowie $\text{DFT von Signal (c)}$ ?
- Im ersten Fall ⇒ ${\rm Re}\big [D(\mu=1)] = 1$ ergibt sich im Zeitbereich die komplexe Exponentialfunktion ⇒ $x(t) = {\rm e}^{+{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}2\pi \hspace{0.05cm}\cdot\hspace{0.05cm} f_0 \hspace{0.05cm}\cdot\hspace{0.05cm} t}$ mit positivem Vorzeichen.
- Im zweiten Fall ⇒ ${\rm Re}\big [d(\nu=1)] = 1$ ergibt sich im Frequenzbereich die komplexe Exponentialfunktion ⇒ $X(f) = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}2\pi \hspace{0.05cm}\cdot\hspace{0.05cm} f/f_0}$ mit negativem Vorzeichen.
- Für ${\rm Re}\big [d(\nu=15)] = 1$ würde sich im Frequenzbereich die komplexe Exponentialfunktion ⇒ $X(f) = {\rm e}^{+{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}2\pi \hspace{0.05cm}\cdot\hspace{0.05cm} f/f_0}$ mit positivem Vorzeichen ergeben.
(12) Neue Einstellung: $\text{DFT von Signal (k) Dreieckimpuls}$. Interpretieren Sie die $d(\nu)$–Belegung und das DFT–Ergebnis.
- Wählen Sie die Betragsdarstellung. $x(t)$ ist symmetrisch um $t=0$ und erstreckt sich von $-T/2$ bis $+T/2$. Es gilt $T_{\rm A} = T/16$. $d(\nu)$–Belegung:
- $d(0)=x(0)= 1$, $d(1)=x(T_{\rm A})= 0.875$, ... , $d(8)=x(8T_{\rm A})= 0$, $d(9)=x(-7T_{\rm A})= 0.125$, ..., $d(15)=x(-T_{\rm A})= 0.875$.
- Im Frequenzbereich: Erst Gleichanteil ⇒ $D(0)$, dann positive Frequenzen ⇒ $D(1) ,\text{ ... },D(8)$, dann negative Frequenzen (gespiegelt) ⇒ $D(9), \text{ ... },D(15)$.
Zur Handhabung des Applets
(A) Parametereingabe per Slider: $\sigma_X$, $\sigma_Y$ und $\rho$
(B) Auswahl: Darstellung von WDF oder VTF
(C) Reset: Einstellung wie beim Programmstart
(D) Höhenlinien darstellen anstelle von „1D-WDF”
(E) Darstellungsbereich für „2D-WDF”
(F) Manipulation der 3D-Grafik (Zoom, Drehen, ...)
(G) Darstellungsbereich für „1D-WDF” bzw. „Höhenlinien”
(H) Manipulation der 2D-Grafik („1D-WDF”)
( I ) Bereich für die Versuchsdurchführung: Aufgabenauswahl
(J) Bereich für die Versuchsdurchführung: Aufgabenstellung
(K) Bereich für die Versuchsdurchführung: Musterlösung einblenden
( L) Bereich für die Versuchsdurchführung: Musterlösung
Werte–Ausgabe über Maussteuerung (sowohl bei 2D als auch bei 3D)
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2003 von Ji Li im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2019 wurde das Programm von Carolin Mirschina im Rahmen einer Werkstudententätigkeit auf „HTML5” umgesetzt und neu gestaltet (Betreuer: Tasnád Kernetzky).
Die Umsetzung dieses Applets auf HTML 5 wurde durch Studienzuschüsse der Fakultät EI der TU München finanziell unterstützt. Wir bedanken uns.