Difference between revisions of "Applets:Frequenzgang und Impulsantwort"
m (Text replacement - "„" to """) |
|||
| (35 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | {{LntAppletLinkEn|frequImpResp_en}} | |
| − | |||
| − | {{ | ||
==Programmbeschreibung== | ==Programmbeschreibung== | ||
| − | <br> | + | <br> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Dargestellt werden reelle und symmetrische Tiefpässe $H(f)$ und die dazugehörigen Impulsantworten $h(t)$, nämlich | ||
| + | *Gauß–Tiefpass (englisch: ''Gaussian low–pass''), | ||
| + | *Rechteck–Tiefpass (englisch: ''Rectangular low–pass''), | ||
| + | *Dreieck–Tiefpass (englisch: ''Triangular low–pass''), | ||
| + | *Trapez–Tiefpass (englisch: ''Trapezoidal low–pass''), | ||
| + | *Cosinus–Rolloff–Tiefpass (englisch: ''Cosine-rolloff low–pass''), | ||
| + | *Cosinus-Quadrat-Tiefpass (englisch: ''Cosine-rolloff -squared Low–pass''). | ||
| − | |||
| + | Das aufzurufende Applet verwendet die englischen Begriffe im Gegensatz zu dieser deutschen Beschreibung. | ||
| − | + | Die englische Beschreibung finden Sie unter [[englische Version: Frequency & Pulse response]] (ist derzeit noch nicht realisiert). | |
| − | |||
| − | |||
| − | |||
| − | + | Weiter ist zu beachten: | |
| − | $ | + | * Die Funktionen $H(f)$ bzw. $h(t)$ werden für bis zu zwei Parametersätzen in jeweils einem Diagramm dargestellt. |
| + | * Die orangenfarbenen ("roten") Kurven und Zahlenangaben gelten für den linken Parametersatz, die blauen für den rechten Parametersatz. | ||
| + | * Die Abszissen $t$ (Zeit) und $f$ (Frequenz) sowie die Ordinaten $H(f)$ und $h(t)$ sind jeweils normiert. | ||
| − | |||
| Line 31: | Line 28: | ||
<br> | <br> | ||
===Frequenzgang $H(f)$ und Impulsantwort $h(t)$=== | ===Frequenzgang $H(f)$ und Impulsantwort $h(t)$=== | ||
| − | *Der [[ | + | *Der [[Linear_and_Time_Invariant_Systems/Systembeschreibung_im_Frequenzbereich#.C3.9Cbertragungsfunktion_-_Frequenzgang|Frequenzgang]] (oder auch die ''Übertragungsfunktion'') eines linearen zeitinvarianten Übertragungssystems $H(f)$ gibt das Verhältnis zwischen dem Ausgangsspektrum $Y(f)$ und dem dem Eingangsspektrum $X(f)$ an: |
| − | *Die Eigenschaften von $H(f)$ werden im Zeitbereich durch die [[ | + | :$$H(f) = \frac{Y(f)}{X(f)}.$$ |
| + | *Ist das Übertragungsverhalten bei tiefen Frequenzen besser als bei höheren, so spricht man von einem '''Tiefpass''' (englisch: ''Low-pass''). | ||
| + | *Die Eigenschaften von $H(f)$ werden im Zeitbereich durch die [[Linear_and_Time_Invariant_Systems/Systembeschreibung_im_Zeitbereich#Impulsantwort|Impulsantwort]] $h(t)$ ausgedrückt. Entsprechend dem [[Signal_Representation/Fourier_Transform_and_Its_Inverse#Das_zweite_Fourierintegral|zweiten Fourierintegral]] gilt: | ||
:$$h(t)={\rm IFT} [H(f)] = \int_{-\infty}^{+\infty}H(f)\cdot {\rm e}^{+{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}f\hspace{1cm} | :$$h(t)={\rm IFT} [H(f)] = \int_{-\infty}^{+\infty}H(f)\cdot {\rm e}^{+{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}f\hspace{1cm} | ||
{\rm IFT}\hspace{-0.1cm}: \rm Inverse \ Fouriertransformation.$$ | {\rm IFT}\hspace{-0.1cm}: \rm Inverse \ Fouriertransformation.$$ | ||
| − | + | *Die Gegenrichtung wird durch das [[Signal_Representation/Fourier_Transform_and_Its_Inverse#Das_erste_Fourierintegral|erste Fourierintegral]] beschrieben: | |
| − | + | :$$H(f)={\rm FT} [h(t)] = \int_{-\infty}^{+\infty}h(t)\cdot {\rm e}^{-{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}t\hspace{1cm} | |
| − | :$$ | ||
\rm FT\hspace{-0.1cm}: \ Fouriertransformation.$$ | \rm FT\hspace{-0.1cm}: \ Fouriertransformation.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
*In allen Beispielen verwenden wir reelle und gerade Funktionen. Somit gilt: | *In allen Beispielen verwenden wir reelle und gerade Funktionen. Somit gilt: | ||
| − | :$$ | + | :$$h(t)=\int_{-\infty}^{+\infty}H(f)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}f \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ H(f)=\int_{-\infty}^{+\infty}h(t)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}t .$$ |
| − | *$ | + | *Bei einem Vierpol ⇒ $X(f)$ und $Y(f)$ haben gleiche Einheiten] ist $Y(f)$ dimensionslos. Die Einheit der Impulsantwort ist $\rm 1/s$. Es gilt zwar $\rm 1/s = 1 \ Hz$, aber die Einheit "Hertz" ist in diesem Zusammenhang unüblich. |
| − | *Der Zusammenhang zwischen diesem Modul & | + | *Der Zusammenhang zwischen diesem Modul "Frequenzgang & Impulsantwort" und dem ähnlich aufgebauten Applet [[Applets:Impulse_und_Spektren]] basiert auf dem [[Signal_Representation/Fourier_Transform_Laws#Vertauschungssatz|Vertauschungssatz]]. |
| − | *Alle Zeiten sind auf eine Normierungszeit $T$ normiert und alle Frequenzen auf $1/T \Rightarrow$ die | + | *Alle Zeiten sind auf eine Normierungszeit $T$ normiert und alle Frequenzen auf $1/T \Rightarrow$ die Impulsantwortwerte $h(t)$ müssen noch durch die Normierungszeit $T$ dividiert werden. |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel:}$ Stellt man einen | + | $\text{Beispiel:}$ Stellt man einen Rechteck–Tiefpass mit Höhe $K_1 = 1$ und äquivalenter Bandbreite $\Delta f_1 = 1$ ein, so ist der Frequenzgang $H_1(f)$ im Bereich $-1 < f < 1$ gleich $1$ und außerhalb dieses Bereichs gleich $0$. Die Impulsantwort $h_1(t)$ verläuft si–förmig mit $h_1(t= 0) = 1$ und der ersten Nullstelle bei $t=1$. |
| − | + | Mit dieser Einstellung soll nun ein Rechteck–Tiefpass mit $K = 1.5$ und $\Delta f = 2 \ \rm kHz$ nachgebildet werden, wobei wir die Normierungszeit $T= 1 \ \rm ms$. Dann liegt die erste Nullstelle bei $t=0.5\ \rm ms$ und das Impulsantwortmaximum ist dann $h(t= 0) = 3 \cdot 10^3 \ \rm 1/s$.}} | |
===Gauß–Tiefpass $\Rightarrow$ Gaussian Low–pass === | ===Gauß–Tiefpass $\Rightarrow$ Gaussian Low–pass === | ||
| − | * | + | *Der Gauß–Tiefpass lautet mit der Höhe $K$ und der (äquivalenten) Bandbreite $\Delta f$: |
| − | :$$ | + | :$$H(f)=K\cdot {\rm e}^{-\pi\cdot(f/\Delta f)^2}.$$ |
| − | *Die äquivalente | + | *Die äquivalente Bandbreite $\Delta f$ ergibt sich aus dem flächengleichen Rechteck. |
| − | *Der Wert bei $ | + | *Der Wert bei $f = \Delta f/2$ ist um den Faktor $0.456$ kleiner als der Wert bei $f=0$. |
| − | *Für die | + | *Für die Impulsantwort erhält man gemäß der Fourierrücktransformation: |
| − | :$$ | + | :$$h(t)=K\cdot \Delta f \cdot {\rm e}^{-\pi(t\cdot \Delta f)^2} .$$ |
| − | *Je kleiner | + | *Je kleiner $\Delta f$ ist, um so breiter und niedriger ist die Impulsantwort ⇒ [[Signal_Representation/Fourier_Transform_Laws#Reziprozit.C3.A4tsgesetz_von_Zeitdauer_und_Bandbreite|Reziprozitätsgesetz von Bandbreite und Impulsdauer]]. |
| − | *Sowohl $ | + | *Sowohl $H(f)$ als auch $h(t)$ sind zu keinem $f$- bzw. $t$-Wert exakt gleich Null. |
| − | *Für praktische Anwendungen kann der Gaußimpuls jedoch in Zeit und Frequenz als begrenzt angenommen werden. Zum Beispiel ist $ | + | *Für praktische Anwendungen kann der Gaußimpuls jedoch in Zeit und Frequenz als begrenzt angenommen werden. Zum Beispiel ist $h(t)$ bereits bei $t=1.5 \cdot \Delta t$ auf weniger als $0.1\% $ des Maximums abgefallen. |
===Idealer (rechteckförmiger) Tiefpass $\Rightarrow$ Rectangular Low–pass === | ===Idealer (rechteckförmiger) Tiefpass $\Rightarrow$ Rectangular Low–pass === | ||
| − | * | + | *Der Rechteck–Tiefpass lautet mit der Höhe $K$ und der (äquivalenten) Bandbreite $\Delta f$: |
| + | |||
| + | :$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K /2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| < \Delta f/2,} \\ {\left| \hspace{0.05cm}f\hspace{0.05cm} \right| = \Delta f/2,} \\ {\left|\hspace{0.05cm} f \hspace{0.05cm} \right| > \Delta f/2.} \\ \end{array}$$ | ||
| − | :$$ | + | *Der $\pm \Delta f/2$–Wert liegt mittig zwischen links- und rechtsseitigem Grenzwert. |
| + | *Für die Impulsantwort $h(t)$ erhält man entsprechend den Gesetzmäßigkeiten der Fourierrücktransformation (2. Fourierintegral): | ||
| + | :$$h(t)=K\cdot \Delta f \cdot {\rm si}(\pi\cdot \Delta f \cdot t) \quad \text{mit} \ {\rm si}(x)={\sin(x)}/{x}.$$ | ||
| + | *Der $h(t)$–Wert bei $t=0$ ist gleich der Rechteckfläche des Frequenzgangs. | ||
| + | *Die Impulsantwort besitzt Nullstellen in äquidistanten Abständen $1/\Delta f$. | ||
| + | *Das Integral über die Impulsantwort $h(t)$ ist gleich dem Frequenzgang $H(f)$ bei der Frequenz $f=0$, also gleich $K$. | ||
| − | + | ===Dreieck–Tiefpass $\Rightarrow$ Triangular Low–pass=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *Der Dreieck–Tiefpass lautet mit der Höhe $K$ und der (äquivalenten) Bandbreite $\Delta f$: | |
| − | |||
| − | :$$ | + | :$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot \Big(1-\frac{|f|}{\Delta f}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| < \Delta f,} \\ {\left| \hspace{0.05cm}f\hspace{0.05cm} \right| \ge \Delta f.} \\ \end{array}$$ |
| − | *Die absolute | + | *Die absolute physikalische Bandbreite $B$ ⇒ nur positive Frequenzen] ist ebenfalls gleich $\Delta f$, also so groß wie beim Rechteck–Tiefpass. |
| − | *Für die | + | *Für die Impulsantwort $h(t)$ erhält man gemäß der Fouriertransformation: |
| − | :$$ | + | :$$h(t)=K\cdot \Delta f \cdot {\rm si}^2(\pi\cdot \Delta f \cdot t) \quad \text{mit} \ {\rm si}(x)={\sin(x)}/{x}.$$ |
| − | * | + | *$H(f)$ kann man als Faltung zweier Rechteckfunktionen (jeweils mit Breite $\Delta f$) darstellen. |
| − | *Daraus folgt: $ | + | *Daraus folgt: $h(t)$ beinhaltet anstelle der ${\rm si}$-Funktion die ${\rm si}^2$-Funktion. |
| − | *$ | + | *$h(t)$ weist somit ebenfalls Nullstellen im äquidistanten Abständen $1/\Delta f$ auf. |
| − | *Der asymptotische Abfall von $ | + | *Der asymptotische Abfall von $h(t)$ erfolgt hier mit $1/t^2$, während zum Vergleich beim Rechteck–Tiefpass $h(t)$ mit $1/t$ abfällt. |
===Trapez–Tiefpass $\Rightarrow$ Trapezoidal Low–pass === | ===Trapez–Tiefpass $\Rightarrow$ Trapezoidal Low–pass === | ||
| − | + | Der Trapez–Tiefpass lautet mit der Höhe $K$ und den Eckfrequenzen $f_1$ und $f_2$: | |
| − | :$$ | + | :$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \frac{f_2-|f|}{f_2-f_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| \le f_1,} \\ {f_1\le \left| \hspace{0.05cm}f\hspace{0.05cm} \right| \le f_2,} \\ {\left|\hspace{0.05cm} f \hspace{0.05cm} \right| \ge f_2.} \\ \end{array}$$ |
| − | *Für die äquivalente | + | *Für die äquivalente Bandbreite (flächengleiches Rechteck) gilt: $\Delta f = f_1+f_2$. |
| − | *Der Rolloff-Faktor (im | + | *Der Rolloff-Faktor (im Frequenzbereich) kennzeichnet die Flankensteilheit: |
| − | :$$r=\frac{ | + | :$$r=\frac{f_2-f_1}{f_2+f_1}.$$ |
| − | *Der Sonderfall $r=0$ entspricht dem | + | *Der Sonderfall $r=0$ entspricht dem Rechteck–Tiefpass und der Sonderfall $r=1$ dem Dreieck–Tiefpass. |
| − | *Für die | + | *Für die Impulsantwort erhält man gemäß der Fourierrücktransformation: |
| − | :$$ | + | :$$h(t)=K\cdot \Delta f \cdot {\rm si}(\pi\cdot \Delta f \cdot t)\cdot {\rm si}(\pi \cdot r \cdot \Delta f \cdot t) \quad \text{mit} \ {\rm si}(x)={\sin(x)}/{x}.$$ |
| − | *Der asymptotische Abfall von $ | + | *Der asymptotische Abfall von $h(t)$ liegt zwischen $1/t$ (für Rechteck–Tiefpass oder $r=0$) und $1/t^2$ (für Dreieck–Tiefpass oder $r=1$). |
===Cosinus-Rolloff-Tiefpass $\Rightarrow$ Cosine-rolloff Low–pass === | ===Cosinus-Rolloff-Tiefpass $\Rightarrow$ Cosine-rolloff Low–pass === | ||
| − | + | Der Cosinus–Rolloff–Tiefpass lautet mit der Höhe $K$ und den Eckfrequenzen $f_1$ und $f_2$: | |
| − | :$$ | + | :$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \cos^2\Big(\frac{|f|-f_1}{f_2-f_1}\cdot \frac{\pi}{2}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| \le f_1,} \\ {f_1\le \left| \hspace{0.05cm}f\hspace{0.05cm} \right| \le f_2,} \\ {\left|\hspace{0.05cm} f \hspace{0.05cm} \right| \ge f_2.} \\ \end{array}$$ |
| − | *Für die äquivalente | + | *Für die äquivalente Bandbreite (flächengleiches Rechteck) gilt: $\Delta f = f_1+f_2$. |
| − | *Der Rolloff-Faktor (im | + | *Der Rolloff-Faktor (im Frequenzbereich) kennzeichnet die Flankensteilheit: |
| − | :$$r=\frac{ | + | :$$r=\frac{f_2-f_1}{f_2+f_1}.$$ |
| − | *Der Sonderfall $r=0$ entspricht dem | + | *Der Sonderfall $r=0$ entspricht dem Rechteck–Tiefpass der Sonderfall $r=1$ dem Cosinus-Quadrat-Tiefpass. |
| − | *Für die | + | *Für die Impulsantwort erhält man gemäß der Fourierrücktransformation: |
| − | :$$ | + | :$$h(t)=K\cdot \Delta f \cdot \frac{\cos(\pi \cdot r\cdot \Delta f \cdot t)}{1-(2\cdot r\cdot \Delta f \cdot t)^2} \cdot {\rm si}(\pi \cdot \Delta f \cdot t).$$ |
| − | *Je größer der Rolloff-Faktor $r$ ist, desto schneller nimmt $ | + | *Je größer der Rolloff-Faktor $r$ ist, desto schneller nimmt $h(t)$ asymptotisch mit $t$ ab. |
| − | ===Cosinus-Quadrat-Tiefpass | + | ===Cosinus-Quadrat-Tiefpass $\Rightarrow$ Cosine-rolloff -squared Low–pass === |
| − | *Dies ist ein Sonderfall des Cosinus | + | *Dies ist ein Sonderfall des Cosinus–Rolloff–Tiefpasses und ergibt sich aus diesem für $r=1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}f_1=0, f_2= \Delta f$: |
| − | :$$ | + | :$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot \cos^2\Big(\frac{|f|\cdot \pi}{2\cdot \Delta f}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| < \Delta f,} \\ {\left| \hspace{0.05cm}f\hspace{0.05cm} \right| \ge \Delta f.} \\ \end{array}$$ |
| − | *Für die | + | *Für die Impulsantwort erhält man gemäß der Fourierrücktransformation: |
| − | :$$ | + | :$$h(t)=K\cdot \Delta f \cdot {\pi}/{4}\cdot \big [{\rm si}(\pi(\Delta f\cdot t +0.5))+{\rm si}(\pi(\Delta f\cdot t -0.5))\big ]\cdot {\rm si}(\pi \cdot \Delta f \cdot t).$$ |
| − | *Wegen der letzten ${\rm si}$-Funktion ist $ | + | *Wegen der letzten ${\rm si}$-Funktion ist $h(t)=0$ für alle Vielfachen von $T=1/\Delta f$ ⇒ Die äquidistanten Nulldurchgänge des Cosinus–Rolloff–Tiefpasses bleiben erhalten. |
| − | *Aufgrund des Klammerausdrucks weist $ | + | *Aufgrund des Klammerausdrucks weist $h(t)$ nun weitere Nulldurchgänge bei $t=\pm1.5 T$, $\pm2.5 T$, $\pm3.5 T$, ... auf. |
| − | *Für | + | *Für $t=\pm T/2$ hat die Impulsanwort den Wert $K\cdot \Delta f/2$. |
| − | *Der asymptotische Abfall von $ | + | *Der asymptotische Abfall von $h(t)$ verläuft in diesem Sonderfall mit $1/t^3$. |
==Vorschlag für die Versuchsdurchführung== | ==Vorschlag für die Versuchsdurchführung== | ||
<br> | <br> | ||
| − | + | "Rot" bezieht sich stets auf den ersten Parametersatz ⇒ $H_1(f) \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\ h_1(t)$ und "Blau" auf den zweiten ⇒ $H_2(f) \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\ h_2(t)$. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(1)''' Vergleichen Sie den '''roten Gauß–Tiefpass''' $(K_1 = 1, \Delta f_1 = 1)$ mit dem '''blauen Rechteck–Tiefpass''' $( | + | '''(1)''' Vergleichen Sie den '''roten Gauß–Tiefpass''' $(K_1 = 1, \Delta f_1 = 1)$ mit dem '''blauen Rechteck–Tiefpass''' $(K_2 = 1, \Delta f_2 = 1)$ ⇒ Voreinstellung ] und beantworten Sie folgende Fragen:<br> |
| − | + | *Welche Signale $y(t)$ treten am Ausgang der Tiefpässe auf, wenn am Eingang das Signal $x(t) = 2 \cdot \cos (2\pi f_0 t -\varphi_0)$ mit $f_0 = 0.5$ anliegt? | |
| − | + | *Welche Unterschiede ergeben sich bei beiden Tiefpässen mit $f_0 = 0.5 \pm f_\varepsilon$ und $f_\varepsilon \ne 0, \ f_\varepsilon \to 0$?}} | |
| − | + | *In beiden Fällen gilt $y(t) = A \cdot \cos (2\pi f_0 t -\varphi_0)$ mit $A = 2 \cdot H(f = f_0) \ \Rightarrow \ A_1 = 2 \cdot 0.456 = 0.912, A_2 = 2 \cdot 0.5 =1.000$. Die Phase $\varphi_0$ bleibt erhalten. | |
| − | + | *Beim Gauß–Tiefpass gilt weiterhin $ A_1 = 0.912$. Beim Rechteck–Tiefpass ist $A_2 = 0$ für $f_0 = 0.5000\text{...}001$ und $A_2 = 2$ für $f_0 = 0.4999\text{...}999$. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(2)''' Lassen Sie die Einstellungen unverändert. Welcher Tiefpass kann das [[ | + | '''(2)''' Lassen Sie die Einstellungen unverändert. Welcher Tiefpass kann das [[Digital_Signal_Transmission/Eigenschaften_von_Nyquistsystemen#Erstes_Nyquistkriterium_im_Zeitbereich|erste Nyquistkriterium]] oder das [[Digital_Signal_Transmission/Eigenschaften_von_Nyquistsystemen#Zweites_Nyquistkriterium|zweite Nyquistkriterium]] erfüllen, wenn $H(f)$ den Gesamtfrequenzgang von Sender, Kanal und Empfangsfilter bezeichnet?}} |
| − | *Um das erste Nyquistkriterium zu erfüllen, muss die Impulsantwort $h(t)$ äquidistante Nulldurchgänge bei Vielfachen der (normierten) Zeit $t = 1, 2$, ... aufweisen. Die Impulsantwort $h(t) = {\rm si}(\pi | + | *Um das erste Nyquistkriterium zu erfüllen, muss die Impulsantwort $h(t)$ äquidistante Nulldurchgänge bei Vielfachen der (normierten) Zeit $t = 1, 2$, ... aufweisen. Die Impulsantwort $h(t) = {\rm si}(\pi \cdot \Delta f \cdot t)$ des Rechteck–Tiefpasses erfüllt dieses Kriterium mit $\Delta f = 1$. Dagegen ist beim Gauß–Tiefpass das erste Nyquistkriterium nie erfüllt und es kommt immer zu [[Digital_Signal_Transmission/Ursachen_und_Auswirkungen_von_Impulsinterferenzen|Impulsinterferenzen]]. |
| − | *Das zweite Nyquistkriterium erfüllt der Rechteck–Tiefpass | + | *Das zweite Nyquistkriterium erfüllt der Rechteck–Tiefpass ebenso nicht wie der Gauß–Tiefpass. |
| − | |||
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(3)''' Vergleichen Sie den '''roten | + | '''(3)''' Vergleichen Sie den '''roten Rechteck–Tiefpass''' $(K_1 = 0.5, \Delta f_1 = 2)$ mit dem '''blauen Rechteck–Tiefpass''' $(K_2 = 1, \Delta f_2 = 1)$ und variieren Sie anschließend $\Delta f_1$ zwischen $2$ und $0.5$. }} |
| + | |||
| − | + | *Bei der Einstellung $\Delta f_1 = 2$ liegen die Nullstellen der Impulsantwort bei Vielfachen von $0.5$. Die Impulsantwort $h_1(t)$ klingt also doppelt so schnell ab als die Impulsantwort $h_2(t)$ des schmalbandigeren Tiefpasses $H_2(f)$. | |
| − | + | *Mit dieser Einstellung gilt $h_1(t = 0) = h_2(t = 0)$, da die Rechteckflächen von $H_1(f)$ und $H_2(f)$ gleich sind. | |
| + | *Verringert man man $\Delta f_1$, so wird die Impulsantwort $h_1(t)$ immer breiter und niedriger. Mit $\Delta f_1 = 0.5$ ist $h_1(t)$ doppelt so breit wie $h_2(t)$, gleichzeitig aber um den Faktor $4$ niedriger. | ||
| − | |||
| − | |||
| + | {{BlaueBox|TEXT= | ||
| + | '''(4)''' Vergleichen Sie den '''roten Trapez–Tiefpass''' $(K_1 = 1, \Delta f_1 = 1, r_1 = 0.5)$ mit dem '''blauen Rechteck–Tiefpass''' $(K_2 = 1, \Delta f_2 = 1)$ und variieren Sie anschließend $r_1$ zwischen $0$ und $1$. }} | ||
| + | |||
| + | |||
| + | *Bei der Einstellung $r_1 = 0.5$ sind die Unterschwinger in der Impulsantwort $h(t)$ beim Trapez–Tiefpass aufgrund des flacheren Flankenabfalls geringer als beim Rechteck–Tiefpass. | ||
| + | *Je kleiner der Roll–off–Faktor $r_1$ wird, desto größer werden die Unterschwinger. Bei $r_1= 0$ ist der Trapez–Tiefpass identisch mit dem Rechteck–Tiefpass ⇒ $h(t)= {\rm si}(\pi \cdot t)$. | ||
| + | *Erhöht man dagegen den Roll–off–Faktor $r_1$, so größer werden die Unterschwinger kleiner. Bei $r_1= 1$ ist der Trapez–Tiefpass identisch mit dem Dreieck–Tiefpass ⇒ $h(t)= {\rm si}^2(\pi \cdot t)$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(5)''' Vergleichen Sie den '''roten Trapez–Tiefpass''' $(K_1 = 1, \Delta f_1 = 1, r_1 = 0.5)$ mit dem '''blauen Cosinus-Rolloff-Tiefpass''' $(K_2 = 1,\Delta f_2 = 1, r_2 = 0.5)$. Variieren Sie $r_2$ zwischen $0$ und $1$. Interpretieren Sie die Impulsantwort $h_2(t)$ für $r_2 = 0.75$. Welcher Tiefpass erfüllt das [[Digital_Signal_Transmission/Eigenschaften_von_Nyquistsystemen#Erstes_Nyquistkriterium_im_Zeitbereich|erste Nyquistkriterium]] ?}} |
| + | |||
| + | *Bei gleichem Rolloff-Faktor $r_1 = r_2= 0.5$ verläuft der Flankenabfall des Cosinus-Rolloff-Tiefpasses $H_2(f)$ um die Frequenz $f = 0.5$ steiler als der Flankenabfall des Trapez–Tiefpasses $H_1(f)$. | ||
| + | *Der Vergleich der zugehörigen Impulsantworten bei gleichem Rolloff-Faktor $r= 0.5$ zeigt, dass $h_2(t)$ für $t > 1$ betragsmäßig größere Anteile besitzt als $h_1(t)$. | ||
| + | *Mit $r_1 = 0.5$ und $r_2 = 0.75$ gilt $H_1(f) \approx H_2(f)$ und damit auch $h_1(t) \approx h_2(t)$. | ||
| + | *Beide Frequenzgänge $H_1(f)$ und $H_2(f)$ erfüllen das erste Nyquistkriterium, da die Funktionen bei $\Delta f = 1$ punktsymmetrisch um den Punkt $f = f_{\rm Nyq} = 1/2, \ H(f_{\rm Nyq}) = K/2$ sind. | ||
| + | *Wegen $\Delta f = 1$ besitzen sowohl $h_1(t)$ als auch $h_2(t)$ Nulldurchgänge bei $\pm 1$, $\pm 2$, ... ⇒ die vertikale Augenöffnung ist in beiden Fällen maximal. | ||
| − | |||
| − | |||
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(6)''' Vergleichen Sie den '''roten Cosinus–Quadrat–Tiefpass''' $(K_1 = 1, \Delta f_1 = 1)$ mit dem '''blauen Cosinus-Rolloff-Tiefpass''' $(K_2 = 1,\Delta f_2 = 1, r_2 = 0.5)$. Variieren Sie $r_2$ zwischen $0$ und $1$. Interpretieren Sie die Ergebnisse. Welcher Tiefpass erfüllt das [[Digital_Signal_Transmission/Eigenschaften_von_Nyquistsystemen#Zweites_Nyquistkriterium|zweite Nyquistkriterium]]?}} |
| + | |||
| + | |||
| + | *Der Cosinus–Quadrat–Tiefpass $H_1(f)$ ist ein Sonderfall Cosinus–Rolloff–Tiefpasses $H_2(f)$ mit Rolloff-Faktor $r_2 =1$. Das erste Nyquistkriterium wird auch mit $r_2 \ne 1$ erfüllt. | ||
| + | *Soll das zweite Nyquistkriterium erfüllt sein, so muss die Impulsantwort weitere Nulldurchgänge bei $t=\pm 1.5$, $\pm 2.5$, $\pm 3.5$, ... aufweisen (nicht jedoch bei $t = \pm 0.5$). | ||
| + | *Für den Cosinus–Quadrat–Tiefpass $H_1(f)$ gilt also $h_1(t=\pm 1) = h_1(t=\pm 1.5) = h_1(t=\pm 2)= h_1(t=\pm 2.5) = \text{...} =0$. Dagegen ist $h_1(t=\pm 0.5) = 0.5$. Der asymptotische Abfall von $h(t)$ verläuft in diesem Sonderfall mit $1/t^3$. | ||
| + | *Kein anderer Tiefpass als der Cosinus–Quadrat–Tiefpass erfüllt das erste und zweite Nyquistkriterium gleichzeitig. Demzufolge ist sowohl die vertikale als auch die horizontale Augenöffnung maximal. | ||
| + | |||
| + | ==Zur Handhabung des Programms== | ||
| + | [[File:Frequenzgang_fertig_version1.png|left]] | ||
| + | '''(A)''' Bereich der graphischen Darstellung für $H(f)$ | ||
| − | + | '''(B)''' Bereich der graphischen Darstellung für $h(t)$ | |
| − | |||
| − | |||
| − | |||
| + | '''(C)''' Variationsmöglichkeit für die graphischen Darstellungen | ||
| − | + | '''(D)''' Parametereingabe per Slider<br> links (rot): "Low–pass 1", rechts (blau): "Low–pass 2" | |
| − | '''( | ||
| + | '''(E)''' Parameter entsprechend der Voreinstellung ⇒ "Reset" | ||
| − | + | '''(F)''' Einstellung von $t_*$ und $f_*$ für Numerikausgabe | |
| − | * | ||
| + | '''(G)''' Numerikausgabe von $H(f_*)$ und $h(t_*)$<br> links (rot): "Low–pass 1", rechts (blau): "Low–pass 2" | ||
| − | + | '''Details zum obigen Punkt (C)''' | |
| − | '''( | + | |
| + | '''(*)''' Zoom–Funktionen "$+$" (Vergrößern), "$-$" (Verkleinern)<br> und $\rm o$ (Zurücksetzen) | ||
| + | '''(*)''' Verschiebe–Funktionen "$\leftarrow$" (Bildausschnitt nach links, <br> Ordinate nach rechts) sowie "$\uparrow$" "$\downarrow$" "$\rightarrow$" | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''Andere Möglichkeiten''': | ||
| − | + | *Bei gedrückter Shifttaste und Scrollen kann im Koordinatensystem gezoomt werden. | |
| − | <br> | + | *Bei gedrückter Shifttaste und gedrückter linker Maustaste kann das Koordinatensystem verschoben werden. |
| + | <br clear = all> | ||
| − | |||
==Über die Autoren== | ==Über die Autoren== | ||
Dieses interaktive Berechnungstool wurde am [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] der [https://www.tum.de/ Technischen Universität München] konzipiert und realisiert. | Dieses interaktive Berechnungstool wurde am [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] der [https://www.tum.de/ Technischen Universität München] konzipiert und realisiert. | ||
| − | *Die erste Version wurde 2005 von [[ | + | *Die erste Version wurde 2005 von [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Studierende#Ji_Li_.28Bachelorarbeit_EI_2003.2C_Diplomarbeit_EI_2005.29|Ji Li]] im Rahmen ihrer Diplomarbeit mit "FlashMX–Actionscript" erstellt (Betreuer: [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_seit_1974.29|Günter Söder]] und [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Dr.-Ing._Klaus_Eichin_.28am_LNT_von_1972-2011.29|Klaus Eichin]]). |
| − | *2017 wurde | + | *2017 wurde "Impulse & Spektren" von [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Studierende#David_Jobst_.28Ingenieurspraxis_Math_2017.29|David Jobst]] im Rahmen seiner Ingenieurspraxis (Betreuer: [[Biographies_and_Bibliographies/Beteiligte_der_Professur_Leitungsgebundene_%C3%9Cbertragungstechnik#Tasn.C3.A1d_Kernetzky.2C_M.Sc._.28bei_L.C3.9CT_seit_2014.29|Tasnád Kernetzky]]) auf "HTML5" umgesetzt und neu gestaltet. |
==Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster== | ==Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster== | ||
| − | {{ | + | {{LntAppletLinkEn|frequImpResp_en}} |
Latest revision as of 16:46, 28 May 2021
Contents
- 1 Programmbeschreibung
- 2 Theoretischer Hintergrund
- 2.1 Frequenzgang $H(f)$ und Impulsantwort $h(t)$
- 2.2 Gauß–Tiefpass $\Rightarrow$ Gaussian Low–pass
- 2.3 Idealer (rechteckförmiger) Tiefpass $\Rightarrow$ Rectangular Low–pass
- 2.4 Dreieck–Tiefpass $\Rightarrow$ Triangular Low–pass
- 2.5 Trapez–Tiefpass $\Rightarrow$ Trapezoidal Low–pass
- 2.6 Cosinus-Rolloff-Tiefpass $\Rightarrow$ Cosine-rolloff Low–pass
- 2.7 Cosinus-Quadrat-Tiefpass $\Rightarrow$ Cosine-rolloff -squared Low–pass
- 3 Vorschlag für die Versuchsdurchführung
- 4 Zur Handhabung des Programms
- 5 Über die Autoren
- 6 Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster
Programmbeschreibung
Dargestellt werden reelle und symmetrische Tiefpässe $H(f)$ und die dazugehörigen Impulsantworten $h(t)$, nämlich
- Gauß–Tiefpass (englisch: Gaussian low–pass),
- Rechteck–Tiefpass (englisch: Rectangular low–pass),
- Dreieck–Tiefpass (englisch: Triangular low–pass),
- Trapez–Tiefpass (englisch: Trapezoidal low–pass),
- Cosinus–Rolloff–Tiefpass (englisch: Cosine-rolloff low–pass),
- Cosinus-Quadrat-Tiefpass (englisch: Cosine-rolloff -squared Low–pass).
Das aufzurufende Applet verwendet die englischen Begriffe im Gegensatz zu dieser deutschen Beschreibung.
Die englische Beschreibung finden Sie unter Englische Version: Frequency & Pulse response (ist derzeit noch nicht realisiert).
Weiter ist zu beachten:
- Die Funktionen $H(f)$ bzw. $h(t)$ werden für bis zu zwei Parametersätzen in jeweils einem Diagramm dargestellt.
- Die orangenfarbenen ("roten") Kurven und Zahlenangaben gelten für den linken Parametersatz, die blauen für den rechten Parametersatz.
- Die Abszissen $t$ (Zeit) und $f$ (Frequenz) sowie die Ordinaten $H(f)$ und $h(t)$ sind jeweils normiert.
Theoretischer Hintergrund
Frequenzgang $H(f)$ und Impulsantwort $h(t)$
- Der Frequenzgang (oder auch die Übertragungsfunktion) eines linearen zeitinvarianten Übertragungssystems $H(f)$ gibt das Verhältnis zwischen dem Ausgangsspektrum $Y(f)$ und dem dem Eingangsspektrum $X(f)$ an:
- $$H(f) = \frac{Y(f)}{X(f)}.$$
- Ist das Übertragungsverhalten bei tiefen Frequenzen besser als bei höheren, so spricht man von einem Tiefpass (englisch: Low-pass).
- Die Eigenschaften von $H(f)$ werden im Zeitbereich durch die Impulsantwort $h(t)$ ausgedrückt. Entsprechend dem zweiten Fourierintegral gilt:
- $$h(t)={\rm IFT} [H(f)] = \int_{-\infty}^{+\infty}H(f)\cdot {\rm e}^{+{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}f\hspace{1cm} {\rm IFT}\hspace{-0.1cm}: \rm Inverse \ Fouriertransformation.$$
- Die Gegenrichtung wird durch das erste Fourierintegral beschrieben:
- $$H(f)={\rm FT} [h(t)] = \int_{-\infty}^{+\infty}h(t)\cdot {\rm e}^{-{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}t\hspace{1cm} \rm FT\hspace{-0.1cm}: \ Fouriertransformation.$$
- In allen Beispielen verwenden wir reelle und gerade Funktionen. Somit gilt:
- $$h(t)=\int_{-\infty}^{+\infty}H(f)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}f \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ H(f)=\int_{-\infty}^{+\infty}h(t)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}t .$$
- Bei einem Vierpol ⇒ $X(f)$ und $Y(f)$ haben gleiche Einheiten] ist $Y(f)$ dimensionslos. Die Einheit der Impulsantwort ist $\rm 1/s$. Es gilt zwar $\rm 1/s = 1 \ Hz$, aber die Einheit "Hertz" ist in diesem Zusammenhang unüblich.
- Der Zusammenhang zwischen diesem Modul "Frequenzgang & Impulsantwort" und dem ähnlich aufgebauten Applet Impulse und Spektren basiert auf dem Vertauschungssatz.
- Alle Zeiten sind auf eine Normierungszeit $T$ normiert und alle Frequenzen auf $1/T \Rightarrow$ die Impulsantwortwerte $h(t)$ müssen noch durch die Normierungszeit $T$ dividiert werden.
$\text{Beispiel:}$ Stellt man einen Rechteck–Tiefpass mit Höhe $K_1 = 1$ und äquivalenter Bandbreite $\Delta f_1 = 1$ ein, so ist der Frequenzgang $H_1(f)$ im Bereich $-1 < f < 1$ gleich $1$ und außerhalb dieses Bereichs gleich $0$. Die Impulsantwort $h_1(t)$ verläuft si–förmig mit $h_1(t= 0) = 1$ und der ersten Nullstelle bei $t=1$.
Mit dieser Einstellung soll nun ein Rechteck–Tiefpass mit $K = 1.5$ und $\Delta f = 2 \ \rm kHz$ nachgebildet werden, wobei wir die Normierungszeit $T= 1 \ \rm ms$. Dann liegt die erste Nullstelle bei $t=0.5\ \rm ms$ und das Impulsantwortmaximum ist dann $h(t= 0) = 3 \cdot 10^3 \ \rm 1/s$.
Gauß–Tiefpass $\Rightarrow$ Gaussian Low–pass
- Der Gauß–Tiefpass lautet mit der Höhe $K$ und der (äquivalenten) Bandbreite $\Delta f$:
- $$H(f)=K\cdot {\rm e}^{-\pi\cdot(f/\Delta f)^2}.$$
- Die äquivalente Bandbreite $\Delta f$ ergibt sich aus dem flächengleichen Rechteck.
- Der Wert bei $f = \Delta f/2$ ist um den Faktor $0.456$ kleiner als der Wert bei $f=0$.
- Für die Impulsantwort erhält man gemäß der Fourierrücktransformation:
- $$h(t)=K\cdot \Delta f \cdot {\rm e}^{-\pi(t\cdot \Delta f)^2} .$$
- Je kleiner $\Delta f$ ist, um so breiter und niedriger ist die Impulsantwort ⇒ Reziprozitätsgesetz von Bandbreite und Impulsdauer.
- Sowohl $H(f)$ als auch $h(t)$ sind zu keinem $f$- bzw. $t$-Wert exakt gleich Null.
- Für praktische Anwendungen kann der Gaußimpuls jedoch in Zeit und Frequenz als begrenzt angenommen werden. Zum Beispiel ist $h(t)$ bereits bei $t=1.5 \cdot \Delta t$ auf weniger als $0.1\% $ des Maximums abgefallen.
Idealer (rechteckförmiger) Tiefpass $\Rightarrow$ Rectangular Low–pass
- Der Rechteck–Tiefpass lautet mit der Höhe $K$ und der (äquivalenten) Bandbreite $\Delta f$:
- $$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K /2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| < \Delta f/2,} \\ {\left| \hspace{0.05cm}f\hspace{0.05cm} \right| = \Delta f/2,} \\ {\left|\hspace{0.05cm} f \hspace{0.05cm} \right| > \Delta f/2.} \\ \end{array}$$
- Der $\pm \Delta f/2$–Wert liegt mittig zwischen links- und rechtsseitigem Grenzwert.
- Für die Impulsantwort $h(t)$ erhält man entsprechend den Gesetzmäßigkeiten der Fourierrücktransformation (2. Fourierintegral):
- $$h(t)=K\cdot \Delta f \cdot {\rm si}(\pi\cdot \Delta f \cdot t) \quad \text{mit} \ {\rm si}(x)={\sin(x)}/{x}.$$
- Der $h(t)$–Wert bei $t=0$ ist gleich der Rechteckfläche des Frequenzgangs.
- Die Impulsantwort besitzt Nullstellen in äquidistanten Abständen $1/\Delta f$.
- Das Integral über die Impulsantwort $h(t)$ ist gleich dem Frequenzgang $H(f)$ bei der Frequenz $f=0$, also gleich $K$.
Dreieck–Tiefpass $\Rightarrow$ Triangular Low–pass
- Der Dreieck–Tiefpass lautet mit der Höhe $K$ und der (äquivalenten) Bandbreite $\Delta f$:
- $$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot \Big(1-\frac{|f|}{\Delta f}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| < \Delta f,} \\ {\left| \hspace{0.05cm}f\hspace{0.05cm} \right| \ge \Delta f.} \\ \end{array}$$
- Die absolute physikalische Bandbreite $B$ ⇒ nur positive Frequenzen] ist ebenfalls gleich $\Delta f$, also so groß wie beim Rechteck–Tiefpass.
- Für die Impulsantwort $h(t)$ erhält man gemäß der Fouriertransformation:
- $$h(t)=K\cdot \Delta f \cdot {\rm si}^2(\pi\cdot \Delta f \cdot t) \quad \text{mit} \ {\rm si}(x)={\sin(x)}/{x}.$$
- $H(f)$ kann man als Faltung zweier Rechteckfunktionen (jeweils mit Breite $\Delta f$) darstellen.
- Daraus folgt: $h(t)$ beinhaltet anstelle der ${\rm si}$-Funktion die ${\rm si}^2$-Funktion.
- $h(t)$ weist somit ebenfalls Nullstellen im äquidistanten Abständen $1/\Delta f$ auf.
- Der asymptotische Abfall von $h(t)$ erfolgt hier mit $1/t^2$, während zum Vergleich beim Rechteck–Tiefpass $h(t)$ mit $1/t$ abfällt.
Trapez–Tiefpass $\Rightarrow$ Trapezoidal Low–pass
Der Trapez–Tiefpass lautet mit der Höhe $K$ und den Eckfrequenzen $f_1$ und $f_2$:
- $$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \frac{f_2-|f|}{f_2-f_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| \le f_1,} \\ {f_1\le \left| \hspace{0.05cm}f\hspace{0.05cm} \right| \le f_2,} \\ {\left|\hspace{0.05cm} f \hspace{0.05cm} \right| \ge f_2.} \\ \end{array}$$
- Für die äquivalente Bandbreite (flächengleiches Rechteck) gilt: $\Delta f = f_1+f_2$.
- Der Rolloff-Faktor (im Frequenzbereich) kennzeichnet die Flankensteilheit:
- $$r=\frac{f_2-f_1}{f_2+f_1}.$$
- Der Sonderfall $r=0$ entspricht dem Rechteck–Tiefpass und der Sonderfall $r=1$ dem Dreieck–Tiefpass.
- Für die Impulsantwort erhält man gemäß der Fourierrücktransformation:
- $$h(t)=K\cdot \Delta f \cdot {\rm si}(\pi\cdot \Delta f \cdot t)\cdot {\rm si}(\pi \cdot r \cdot \Delta f \cdot t) \quad \text{mit} \ {\rm si}(x)={\sin(x)}/{x}.$$
- Der asymptotische Abfall von $h(t)$ liegt zwischen $1/t$ (für Rechteck–Tiefpass oder $r=0$) und $1/t^2$ (für Dreieck–Tiefpass oder $r=1$).
Cosinus-Rolloff-Tiefpass $\Rightarrow$ Cosine-rolloff Low–pass
Der Cosinus–Rolloff–Tiefpass lautet mit der Höhe $K$ und den Eckfrequenzen $f_1$ und $f_2$:
- $$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \cos^2\Big(\frac{|f|-f_1}{f_2-f_1}\cdot \frac{\pi}{2}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| \le f_1,} \\ {f_1\le \left| \hspace{0.05cm}f\hspace{0.05cm} \right| \le f_2,} \\ {\left|\hspace{0.05cm} f \hspace{0.05cm} \right| \ge f_2.} \\ \end{array}$$
- Für die äquivalente Bandbreite (flächengleiches Rechteck) gilt: $\Delta f = f_1+f_2$.
- Der Rolloff-Faktor (im Frequenzbereich) kennzeichnet die Flankensteilheit:
- $$r=\frac{f_2-f_1}{f_2+f_1}.$$
- Der Sonderfall $r=0$ entspricht dem Rechteck–Tiefpass der Sonderfall $r=1$ dem Cosinus-Quadrat-Tiefpass.
- Für die Impulsantwort erhält man gemäß der Fourierrücktransformation:
- $$h(t)=K\cdot \Delta f \cdot \frac{\cos(\pi \cdot r\cdot \Delta f \cdot t)}{1-(2\cdot r\cdot \Delta f \cdot t)^2} \cdot {\rm si}(\pi \cdot \Delta f \cdot t).$$
- Je größer der Rolloff-Faktor $r$ ist, desto schneller nimmt $h(t)$ asymptotisch mit $t$ ab.
Cosinus-Quadrat-Tiefpass $\Rightarrow$ Cosine-rolloff -squared Low–pass
- Dies ist ein Sonderfall des Cosinus–Rolloff–Tiefpasses und ergibt sich aus diesem für $r=1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}f_1=0, f_2= \Delta f$:
- $$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot \cos^2\Big(\frac{|f|\cdot \pi}{2\cdot \Delta f}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| < \Delta f,} \\ {\left| \hspace{0.05cm}f\hspace{0.05cm} \right| \ge \Delta f.} \\ \end{array}$$
- Für die Impulsantwort erhält man gemäß der Fourierrücktransformation:
- $$h(t)=K\cdot \Delta f \cdot {\pi}/{4}\cdot \big [{\rm si}(\pi(\Delta f\cdot t +0.5))+{\rm si}(\pi(\Delta f\cdot t -0.5))\big ]\cdot {\rm si}(\pi \cdot \Delta f \cdot t).$$
- Wegen der letzten ${\rm si}$-Funktion ist $h(t)=0$ für alle Vielfachen von $T=1/\Delta f$ ⇒ Die äquidistanten Nulldurchgänge des Cosinus–Rolloff–Tiefpasses bleiben erhalten.
- Aufgrund des Klammerausdrucks weist $h(t)$ nun weitere Nulldurchgänge bei $t=\pm1.5 T$, $\pm2.5 T$, $\pm3.5 T$, ... auf.
- Für $t=\pm T/2$ hat die Impulsanwort den Wert $K\cdot \Delta f/2$.
- Der asymptotische Abfall von $h(t)$ verläuft in diesem Sonderfall mit $1/t^3$.
Vorschlag für die Versuchsdurchführung
"Rot" bezieht sich stets auf den ersten Parametersatz ⇒ $H_1(f) \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\ h_1(t)$ und "Blau" auf den zweiten ⇒ $H_2(f) \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\ h_2(t)$.
(1) Vergleichen Sie den roten Gauß–Tiefpass $(K_1 = 1, \Delta f_1 = 1)$ mit dem blauen Rechteck–Tiefpass $(K_2 = 1, \Delta f_2 = 1)$ ⇒ Voreinstellung ] und beantworten Sie folgende Fragen:
- Welche Signale $y(t)$ treten am Ausgang der Tiefpässe auf, wenn am Eingang das Signal $x(t) = 2 \cdot \cos (2\pi f_0 t -\varphi_0)$ mit $f_0 = 0.5$ anliegt?
- Welche Unterschiede ergeben sich bei beiden Tiefpässen mit $f_0 = 0.5 \pm f_\varepsilon$ und $f_\varepsilon \ne 0, \ f_\varepsilon \to 0$?
- In beiden Fällen gilt $y(t) = A \cdot \cos (2\pi f_0 t -\varphi_0)$ mit $A = 2 \cdot H(f = f_0) \ \Rightarrow \ A_1 = 2 \cdot 0.456 = 0.912, A_2 = 2 \cdot 0.5 =1.000$. Die Phase $\varphi_0$ bleibt erhalten.
- Beim Gauß–Tiefpass gilt weiterhin $ A_1 = 0.912$. Beim Rechteck–Tiefpass ist $A_2 = 0$ für $f_0 = 0.5000\text{...}001$ und $A_2 = 2$ für $f_0 = 0.4999\text{...}999$.
(2) Lassen Sie die Einstellungen unverändert. Welcher Tiefpass kann das erste Nyquistkriterium oder das zweite Nyquistkriterium erfüllen, wenn $H(f)$ den Gesamtfrequenzgang von Sender, Kanal und Empfangsfilter bezeichnet?
- Um das erste Nyquistkriterium zu erfüllen, muss die Impulsantwort $h(t)$ äquidistante Nulldurchgänge bei Vielfachen der (normierten) Zeit $t = 1, 2$, ... aufweisen. Die Impulsantwort $h(t) = {\rm si}(\pi \cdot \Delta f \cdot t)$ des Rechteck–Tiefpasses erfüllt dieses Kriterium mit $\Delta f = 1$. Dagegen ist beim Gauß–Tiefpass das erste Nyquistkriterium nie erfüllt und es kommt immer zu Impulsinterferenzen.
- Das zweite Nyquistkriterium erfüllt der Rechteck–Tiefpass ebenso nicht wie der Gauß–Tiefpass.
(3) Vergleichen Sie den roten Rechteck–Tiefpass $(K_1 = 0.5, \Delta f_1 = 2)$ mit dem blauen Rechteck–Tiefpass $(K_2 = 1, \Delta f_2 = 1)$ und variieren Sie anschließend $\Delta f_1$ zwischen $2$ und $0.5$.
- Bei der Einstellung $\Delta f_1 = 2$ liegen die Nullstellen der Impulsantwort bei Vielfachen von $0.5$. Die Impulsantwort $h_1(t)$ klingt also doppelt so schnell ab als die Impulsantwort $h_2(t)$ des schmalbandigeren Tiefpasses $H_2(f)$.
- Mit dieser Einstellung gilt $h_1(t = 0) = h_2(t = 0)$, da die Rechteckflächen von $H_1(f)$ und $H_2(f)$ gleich sind.
- Verringert man man $\Delta f_1$, so wird die Impulsantwort $h_1(t)$ immer breiter und niedriger. Mit $\Delta f_1 = 0.5$ ist $h_1(t)$ doppelt so breit wie $h_2(t)$, gleichzeitig aber um den Faktor $4$ niedriger.
(4) Vergleichen Sie den roten Trapez–Tiefpass $(K_1 = 1, \Delta f_1 = 1, r_1 = 0.5)$ mit dem blauen Rechteck–Tiefpass $(K_2 = 1, \Delta f_2 = 1)$ und variieren Sie anschließend $r_1$ zwischen $0$ und $1$.
- Bei der Einstellung $r_1 = 0.5$ sind die Unterschwinger in der Impulsantwort $h(t)$ beim Trapez–Tiefpass aufgrund des flacheren Flankenabfalls geringer als beim Rechteck–Tiefpass.
- Je kleiner der Roll–off–Faktor $r_1$ wird, desto größer werden die Unterschwinger. Bei $r_1= 0$ ist der Trapez–Tiefpass identisch mit dem Rechteck–Tiefpass ⇒ $h(t)= {\rm si}(\pi \cdot t)$.
- Erhöht man dagegen den Roll–off–Faktor $r_1$, so größer werden die Unterschwinger kleiner. Bei $r_1= 1$ ist der Trapez–Tiefpass identisch mit dem Dreieck–Tiefpass ⇒ $h(t)= {\rm si}^2(\pi \cdot t)$.
(5) Vergleichen Sie den roten Trapez–Tiefpass $(K_1 = 1, \Delta f_1 = 1, r_1 = 0.5)$ mit dem blauen Cosinus-Rolloff-Tiefpass $(K_2 = 1,\Delta f_2 = 1, r_2 = 0.5)$. Variieren Sie $r_2$ zwischen $0$ und $1$. Interpretieren Sie die Impulsantwort $h_2(t)$ für $r_2 = 0.75$. Welcher Tiefpass erfüllt das erste Nyquistkriterium ?
- Bei gleichem Rolloff-Faktor $r_1 = r_2= 0.5$ verläuft der Flankenabfall des Cosinus-Rolloff-Tiefpasses $H_2(f)$ um die Frequenz $f = 0.5$ steiler als der Flankenabfall des Trapez–Tiefpasses $H_1(f)$.
- Der Vergleich der zugehörigen Impulsantworten bei gleichem Rolloff-Faktor $r= 0.5$ zeigt, dass $h_2(t)$ für $t > 1$ betragsmäßig größere Anteile besitzt als $h_1(t)$.
- Mit $r_1 = 0.5$ und $r_2 = 0.75$ gilt $H_1(f) \approx H_2(f)$ und damit auch $h_1(t) \approx h_2(t)$.
- Beide Frequenzgänge $H_1(f)$ und $H_2(f)$ erfüllen das erste Nyquistkriterium, da die Funktionen bei $\Delta f = 1$ punktsymmetrisch um den Punkt $f = f_{\rm Nyq} = 1/2, \ H(f_{\rm Nyq}) = K/2$ sind.
- Wegen $\Delta f = 1$ besitzen sowohl $h_1(t)$ als auch $h_2(t)$ Nulldurchgänge bei $\pm 1$, $\pm 2$, ... ⇒ die vertikale Augenöffnung ist in beiden Fällen maximal.
(6) Vergleichen Sie den roten Cosinus–Quadrat–Tiefpass $(K_1 = 1, \Delta f_1 = 1)$ mit dem blauen Cosinus-Rolloff-Tiefpass $(K_2 = 1,\Delta f_2 = 1, r_2 = 0.5)$. Variieren Sie $r_2$ zwischen $0$ und $1$. Interpretieren Sie die Ergebnisse. Welcher Tiefpass erfüllt das zweite Nyquistkriterium?
- Der Cosinus–Quadrat–Tiefpass $H_1(f)$ ist ein Sonderfall Cosinus–Rolloff–Tiefpasses $H_2(f)$ mit Rolloff-Faktor $r_2 =1$. Das erste Nyquistkriterium wird auch mit $r_2 \ne 1$ erfüllt.
- Soll das zweite Nyquistkriterium erfüllt sein, so muss die Impulsantwort weitere Nulldurchgänge bei $t=\pm 1.5$, $\pm 2.5$, $\pm 3.5$, ... aufweisen (nicht jedoch bei $t = \pm 0.5$).
- Für den Cosinus–Quadrat–Tiefpass $H_1(f)$ gilt also $h_1(t=\pm 1) = h_1(t=\pm 1.5) = h_1(t=\pm 2)= h_1(t=\pm 2.5) = \text{...} =0$. Dagegen ist $h_1(t=\pm 0.5) = 0.5$. Der asymptotische Abfall von $h(t)$ verläuft in diesem Sonderfall mit $1/t^3$.
- Kein anderer Tiefpass als der Cosinus–Quadrat–Tiefpass erfüllt das erste und zweite Nyquistkriterium gleichzeitig. Demzufolge ist sowohl die vertikale als auch die horizontale Augenöffnung maximal.
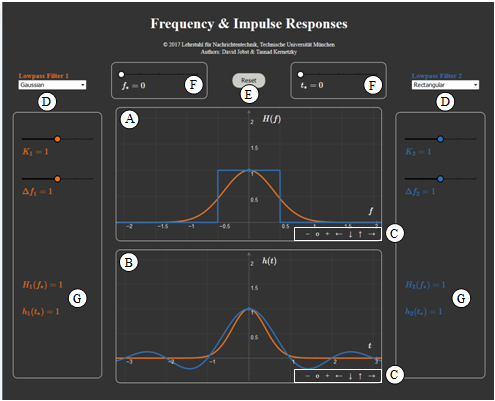
Zur Handhabung des Programms
(A) Bereich der graphischen Darstellung für $H(f)$
(B) Bereich der graphischen Darstellung für $h(t)$
(C) Variationsmöglichkeit für die graphischen Darstellungen
(D) Parametereingabe per Slider
links (rot): "Low–pass 1", rechts (blau): "Low–pass 2"
(E) Parameter entsprechend der Voreinstellung ⇒ "Reset"
(F) Einstellung von $t_*$ und $f_*$ für Numerikausgabe
(G) Numerikausgabe von $H(f_*)$ und $h(t_*)$
links (rot): "Low–pass 1", rechts (blau): "Low–pass 2"
Details zum obigen Punkt (C)
(*) Zoom–Funktionen "$+$" (Vergrößern), "$-$" (Verkleinern)
und $\rm o$ (Zurücksetzen)
(*) Verschiebe–Funktionen "$\leftarrow$" (Bildausschnitt nach links,
Ordinate nach rechts) sowie "$\uparrow$" "$\downarrow$" "$\rightarrow$"
Andere Möglichkeiten:
- Bei gedrückter Shifttaste und Scrollen kann im Koordinatensystem gezoomt werden.
- Bei gedrückter Shifttaste und gedrückter linker Maustaste kann das Koordinatensystem verschoben werden.
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2005 von Ji Li im Rahmen ihrer Diplomarbeit mit "FlashMX–Actionscript" erstellt (Betreuer: Günter Söder und Klaus Eichin).
- 2017 wurde "Impulse & Spektren" von David Jobst im Rahmen seiner Ingenieurspraxis (Betreuer: Tasnád Kernetzky) auf "HTML5" umgesetzt und neu gestaltet.