Difference between revisions of "Aufgaben:4.1:WDF, VTF und Wahrscheinlichkeit"
| Line 8: | Line 8: | ||
:* der [http://en.lntwww.de/Stochastische_Signaltheorie/Wahrscheinlichkeitsdichtefunktion '''Wahrscheinlichkeitsdichtefunktion '''] (WDF), | :* der [http://en.lntwww.de/Stochastische_Signaltheorie/Wahrscheinlichkeitsdichtefunktion '''Wahrscheinlichkeitsdichtefunktion '''] (WDF), | ||
:* der [http://en.lntwww.de/Stochastische_Signaltheorie/Verteilungsfunktion ''' Verteilungsfunktion '''] (VTF). | :* der [http://en.lntwww.de/Stochastische_Signaltheorie/Verteilungsfunktion ''' Verteilungsfunktion '''] (VTF). | ||
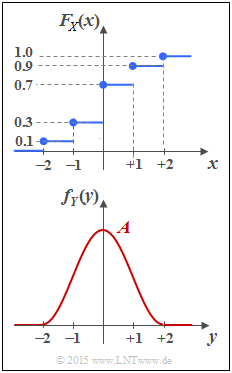
| + | Die obere Darstellung zeigt die Verteilungsfunktion $F_X(x)$ einer wertdiskreten Zufallsgröße ''X''. Die zugehörige WDF $f_X(x)$ ist in der Teilaufgabe (a) zu bestimmen. Die Gleichung | ||
| + | $$ {\rm Pr}(A < X \le B) \hspace{-0.15cm} = \hspace{-0.15cm} F_X(B) - F_X(A) = $$ | ||
| + | $$ =\hspace{-0.15cm} \lim_{\varepsilon \hspace{0.05cm}\rightarrow \hspace{0.05cm}0} \int\limits_{A+\varepsilon}^{B+\varepsilon} \hspace{-0.15cm} f_X(x) \hspace{0.1cm}{\rm d}x $$ | ||
| + | stellt zwei Möglichkeiten dar, um die Wahrscheinlichkeit für das Ereignis „Die Zufallsgröße ''X'' liegt in einem Intervall” aus der VTF bzw. der WDF zu berechnen. | ||
| + | |||
| + | Die untere Grafik zeigt die Wahrscheinlichkeitsdichtefunktion | ||
| + | $$ f_Y(y) = \left\{ \begin{array}{c} \hspace{0.1cm}1/2 \cdot \cos^2(\pi/4 \cdot y) \\ \hspace{0.1cm} 0 \\ \end{array} \right.\quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}l} | y| \le 2, \\ | ||
| + | y < -2 \hspace{0.1cm}{\rm und}\hspace{0.1cm}y > +2 \\ \end{array}$$ | ||
| + | einer wertkontinuierlichen Zufallsgröße Y, die auf den Bereich |''Y''| ≤ 2 begrenzt ist. | ||
| + | |||
| + | Prinzipiell besteht bei der kontinuierlichen Zufallsgröße ''Y'' der gleiche Zusammenhang zwischen WDF, VTF und Wahrscheinlichkeiten wie bei einer diskreten Zufallsgröße. Sie werden trotzdem einige Detailunterschiede feststellen. Beispielsweise kann bei der kontinuierlichen Zufallsgröße ''Y'' in obiger Gleichung auf den Grenzübergang verzichtet werden, und man erhält vereinfacht: | ||
| + | $${\rm Pr}(A \le Y \le B) = F_Y(B) - F_Y(A) =\int_{A}^{B} \hspace{-0.01cm} f_Y(y) | ||
| + | \hspace{0.1cm}{\rm d}y\hspace{0.05cm}$$. | ||
| + | |||
| + | '''Hinweis''': Die Aufgabe dient zur Vorbereitung der in [http://en.lntwww.de/Informationstheorie/Differentielle_Entropie '''Kapitel 4.1'''] dargelegten Thematik. Nützliche Hinweise zur Lösung dieser Aufgabe und weitere Informationen zu den wertkontinuierlichen Zufallsgrößen finden Sie im [http://en.lntwww.de/Stochastische_Signaltheorie '''Kapitel 3'''] des Buches „Stochastische Signaltheorie”. | ||
| + | Gegeben ist zudem das folgende unbstimmte Integral: | ||
| + | $$\int \hspace{0.1cm} \cos^2(A \eta) \hspace{0.1cm}{\rm d}\eta = \frac{\eta}{2} + \frac{1}{4A} \cdot \sin(2A \eta)$$. | ||
===Fragebogen=== | ===Fragebogen=== | ||
Revision as of 17:51, 19 March 2017
Zur Wiederholung einiger wichtiger Grundlagen aus dem Buch stochastischen Signaltheorie beschäftigen wir uns mit
- der Wahrscheinlichkeitsdichtefunktion (WDF),
- der Verteilungsfunktion (VTF).
Die obere Darstellung zeigt die Verteilungsfunktion $F_X(x)$ einer wertdiskreten Zufallsgröße X. Die zugehörige WDF $f_X(x)$ ist in der Teilaufgabe (a) zu bestimmen. Die Gleichung $$ {\rm Pr}(A < X \le B) \hspace{-0.15cm} = \hspace{-0.15cm} F_X(B) - F_X(A) = $$ $$ =\hspace{-0.15cm} \lim_{\varepsilon \hspace{0.05cm}\rightarrow \hspace{0.05cm}0} \int\limits_{A+\varepsilon}^{B+\varepsilon} \hspace{-0.15cm} f_X(x) \hspace{0.1cm}{\rm d}x $$
stellt zwei Möglichkeiten dar, um die Wahrscheinlichkeit für das Ereignis „Die Zufallsgröße X liegt in einem Intervall” aus der VTF bzw. der WDF zu berechnen.
Die untere Grafik zeigt die Wahrscheinlichkeitsdichtefunktion $$ f_Y(y) = \left\{ \begin{array}{c} \hspace{0.1cm}1/2 \cdot \cos^2(\pi/4 \cdot y) \\ \hspace{0.1cm} 0 \\ \end{array} \right.\quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}l} | y| \le 2, \\ y < -2 \hspace{0.1cm}{\rm und}\hspace{0.1cm}y > +2 \\ \end{array}$$ einer wertkontinuierlichen Zufallsgröße Y, die auf den Bereich |Y| ≤ 2 begrenzt ist.
Prinzipiell besteht bei der kontinuierlichen Zufallsgröße Y der gleiche Zusammenhang zwischen WDF, VTF und Wahrscheinlichkeiten wie bei einer diskreten Zufallsgröße. Sie werden trotzdem einige Detailunterschiede feststellen. Beispielsweise kann bei der kontinuierlichen Zufallsgröße Y in obiger Gleichung auf den Grenzübergang verzichtet werden, und man erhält vereinfacht: $${\rm Pr}(A \le Y \le B) = F_Y(B) - F_Y(A) =\int_{A}^{B} \hspace{-0.01cm} f_Y(y) \hspace{0.1cm}{\rm d}y\hspace{0.05cm}$$.
Hinweis: Die Aufgabe dient zur Vorbereitung der in Kapitel 4.1 dargelegten Thematik. Nützliche Hinweise zur Lösung dieser Aufgabe und weitere Informationen zu den wertkontinuierlichen Zufallsgrößen finden Sie im Kapitel 3 des Buches „Stochastische Signaltheorie”. Gegeben ist zudem das folgende unbstimmte Integral: $$\int \hspace{0.1cm} \cos^2(A \eta) \hspace{0.1cm}{\rm d}\eta = \frac{\eta}{2} + \frac{1}{4A} \cdot \sin(2A \eta)$$.
Fragebogen
Musterlösung