Exercise 4.06Z: Signal Space Constellations
Die (mittlere) Fehlerwahrscheinlichkeit eines optimalen Binärsystems lautet:
- $$p_{\rm S} = {\rm Pr}({ \cal E} ) = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right )\hspace{0.05cm}.$$
Hierzu ist anzumerken:
- ${\rm Q}(x)$ bezeichnet die komplementäre Gaußsche Fehlerfunktion (Definition und Approximation):
- $${\rm Q}(x) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2\pi}} \int_{x}^{\infty} {\rm e}^{-u^2/2} \,{\rm d} u \approx \frac{1}{\sqrt{2\pi} \cdot x} \cdot {\rm e}^{-x^2/2} \hspace{0.05cm}.$$
- $d$ gibt den Abstand der beiden Sendesignalpunkte $s_0$ und $s_1$ im Vektorraum an:
- $$d = \sqrt{ || \boldsymbol{ s }_1 - \boldsymbol{ s }_0||^2} \hspace{0.05cm}.$$
- $\sigma_n^2$ ist die Varianz des AWGN–Rauschens nach dem Detektor, der zum Beispiel als Matched–Filter realisiert sein kann.
Es gelte $\sigma_n^2 = N_0/2$.
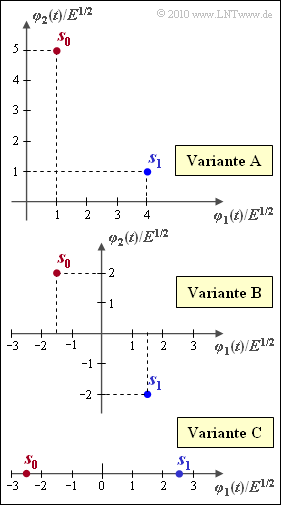
Durch die Grafik sind drei unterschiedliche Signalraumkonstellationen gegeben, nämlich
- Variante $\rm A$: $s_0 = (+1, \, +5), \hspace{0.4cm} s_1 = (+4, \, +1)$,
- Variante $\rm B$: $s_0 = (-1.5, \, +2), \, s_1 = (+1.5, \, -2)$,
- Variante $\rm C$: $s_0 = (-2.5, \, 0), \hspace{0.45cm} s_1 = (+2.5, \, 0)$.
Die jeweils mittlere Energie pro Symbol $(E_{\rm S})$ kann wie folgt berechnet werden:
- $$E_{\rm S} = {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) \cdot || \boldsymbol{ s }_0||^2 + {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_1) \cdot || \boldsymbol{ s }_1||^2\hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Approximation der Fehlerwahrscheinlichkeit.
- Für numerische Berechnungen kann zur Vereinfachung die Energie $E = 1$ gesetzt werden.
- Wenn keine anderslautende Angabe gemacht ist, so kann von gleichwahrscheinlichen Symbolen ausgegangen werden:
- $${\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) = {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_1) = 0.5\hspace{0.05cm}.$$
Fragebogen
Musterlösung
- Die Gleichung gilt dann unabhängig von den Auftrittswahrscheinlichkeiten.
- Im Fall ${\rm Pr}(\boldsymbol{s} = \boldsymbol{s}_0) ≠ {\rm Pr}(\boldsymbol{s} = \boldsymbol{s}_1)$ kann durch eine Verschiebung der Entscheiderschwelle eine kleinere Fehlerwahrscheinlichkeit erzielt werden.
(2) Der Rauscheffektivwert $\sigma_n$ und damit auch die Signalenergie $E = \sigma_n^2$ sind für alle drei betrachteten Varianten gleich. Gleiches gilt für die Distanz der Signalraumpunkte. Für die Variante $\rm A$ gilt zum Beispiel:
- $$d = \sqrt{ || \boldsymbol{ s }_1 - \boldsymbol{ s }_0||^2} = \sqrt{ E \cdot (4-1)^2 + E \cdot (1-5)^2} = 5 \cdot \sqrt{E}\hspace{0.05cm}.$$
Durch die Verschiebung des Koordinatensystems ändert sich am Absand zwischen $\boldsymbol{s}_0$ und $\boldsymbol{s}_1$ nichts (Variante $\rm B$), und auch bei Variante $\rm C$ (nach Drehung) ergibt sich der gleiche Abstand.
Richtig ist also der Lösungsvorschlag 4:
- Durch eine Drehung des Koordinatensystems kann man bei einem Binärsystem $(M = 2)$ stets mit einer Basisfunktion $(N = 1)$ auskommen.
- Da das zweidimensionale Rauschen zirkulär symmetrisch ist ⇒ gleiche Streuung $\sigma_n$ in alle Richtungen, kann auch der Rauschterm wie im Kapitel Fehlerwahrscheinlichkeit bei Basisbandübertragung eindimensional beschrieben werden.
(3) Für alle hier betrachteten Varianten gilt, also auch für die Variante $\rm A$:
- $$p_{\rm S} = {\rm Pr}({ \cal E} ) = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right )= {\rm Q} \left ( \frac{5/2 \cdot \sqrt{E}}{\sigma_n} \right ) = {\rm Q}(2.5)\hspace{0.05cm}.$$
Mit der angegebenen Näherung erhält man
- $$p_{\rm S} = \frac{1}{\sqrt{2\pi} \cdot 2.5} \cdot {\rm e}^{-2.5^2/2} \hspace{0.1cm} \hspace{0.15cm}\underline {\approx 0.7 \%}\hspace{0.05cm}.$$
(4) Bei der Variante $\rm C$ ergibt sich für die mittlere Energie pro Symbol:
- $$E_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) \cdot (-2.5 \cdot \sqrt{E})^2 + {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_1) \cdot (+ 2.5 \cdot \sqrt{E})^2 = \left [ {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) + {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) \right ] \cdot 6.25 \cdot E = 6.25 \cdot E$$
- $$\Rightarrow \hspace{0.3cm} E = \frac {E_{\rm S}}{6.25} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sqrt{E}= \frac {\sqrt{E_{\rm S}}}{2.5} \hspace{0.05cm}.$$
Setzt man dieses Ergebnis in die unter (3) gefundene Gleichung ein, so erhält man mit $\sigma_n^2 = N_0/2$:
- $$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Q} \left ( \frac{2.5 \cdot \sqrt{E}}{\sigma_n} \right )= {\rm Q} \left ( \frac{ \sqrt{E_{\rm S}}}{\sigma_n} \right ) = {\rm Q} \left ( \frac{ \sqrt{2 \cdot E_{\rm S}}}{N_0} \right ) ={\rm Q} \left ( \sqrt{\frac{ 2 \cdot 6.25 \cdot 10^{-6}\,{\rm Ws}}{2 \cdot 10^{-6}\,{\rm W/Hz}}} \right ) ={\rm Q}(2.5) \hspace{0.1cm} \hspace{0.15cm}\underline {\approx 0.7 \%}\hspace{0.05cm}. $$
(5) Durch Drehung des Koordinatensystems ändert sich nichts an den Energieverhältnissen. Deshalb erhält man wieder $p_{\rm S} \ \underline {\approx 0.7\%}$.
(6) Bei der Variante $\rm A$ ist die mittlere Energie pro Symbol
- $$E_{\rm S} = {1}/{2} \cdot \left [ (1^2 + 5^2) \cdot E + (4^2 + 1^2) \cdot E \right ] = 21.5 \cdot E \hspace{0.05cm}. $$
Der Abstand von der Schwelle, die bei gleichwahrscheinlichen Symbolen in der Mitte zwischen $\boldsymbol{s}_0$ und $\boldsymbol{s}_1$ liegen sollte, ist wie bei den anderen Varianten $d/2 = 2.5 \cdot E^{\rm 1/2}$. Mit $\sigma_n^2 = N_0/2$ erhält man somit die Bestimmungsgleichung:
- $$p_{\rm S} = {\rm Q} \left ( \frac{ 2.5 \cdot \sqrt{E}}{\sqrt{N_0/2}} \right ) ={\rm Q}(2.5)\approx 0.7 \cdot 10^{-2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sqrt{\frac {2E}{N_0}} = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac {E}{N_0} = 0.5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\frac {E_{\rm S}}{21.5 \cdot N_0} = 0.5$$
- $$\Rightarrow \hspace{0.3cm} {E_{\rm S}} = 0.5 \cdot {21.5 \cdot N_0} \hspace{0.1cm} \hspace{0.15cm}\underline { = 21.5 \cdot 10^{-6}\,{\rm Ws}}\hspace{0.05cm}.$$
Das bedeutet: Bei der Variante $\rm A$ ist gegenüber den beiden anderen Symbolen eine um den Faktor $3.44$ größere mittlere Symbolenergie $E_{\rm S}$ erforderlich, um die gleiche Fehlerwahrscheinlichkeit $p_{\rm S} = 0.7%$ zu erzielen.
- Das heißt: Diese Signalraumkonstellation ist sehr ungünstig. Es ergibt sich ein sehr großes $E_{\rm S}$, ohne dass gleichzeitig der Abstand $d$ vergrößert wird.
- Mit $E_{\rm S} = 6.25 \cdot 10^{\rm –6} \ \rm Ws$ würde sich dagegen $p_{\rm S} = {\rm Q}(2.5/3.44^{\rm 1/2}) \approx {\rm Q}(1.35) \approx 9\%$ ergeben.
- Das heißt: Die Fehlerwahrscheinlichkeit würde um mehr als eine Zehnerpotenz größer.