Exercise 1.07: Check and Generator Matrix of the HC (7, 4, 3)

Parity-check equations of the
$(7, 4, 3)$ Hamming code

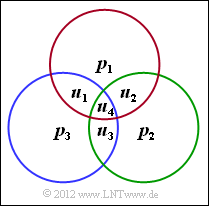
The graph shows the test equations of the $(7, 4, 3)$ Hamming code, which has already been considered in detail in the Exercise 1.6 and described using the code table.

In this task, this code is now characterized by two matrices - as is common in channel coding:

The parity-check matrix $\boldsymbol{\rm H}$ is a matrix with $m = n - k$ rows and $n$ columns. It describes the $m = 3$ parity-check equations, where the first row refers to the elements of the red circle and the second row refers to those of the green circle. The last row gives the modulo-2 sum of the blue circle.

A second description possibility is provided by the generator matrix $ \boldsymbol{\rm G}$ with $k$ rows and $n$ columns. It gives the relationship between the information words $ \underline{u}$ and the code words $\underline{x}$ :

$$ \underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} \hspace{0.05cm}.$$

From this and from the equation $ \boldsymbol{\rm H} · \underline{x}^{\rm T} = \underline{0}$ the relation between the parity-check matrix $ \boldsymbol{\rm H}$ and the generator matrix $ \boldsymbol{\rm G}$ can be established:

$$\underline{x}^{\rm T} = { \boldsymbol{\rm G}}^{\rm T} \cdot \underline{u}^{\rm T} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} { \boldsymbol{\rm H}} \cdot { \boldsymbol{\rm G}}^{\rm T} \cdot \underline{u}^{\rm T} = \underline{0}\hspace{0.5cm} \forall \hspace{0.15cm}\underline{u} \in {\rm GF}(2^k)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} { \boldsymbol{\rm H}} \cdot { \boldsymbol{\rm G}}^{\rm T} = { \boldsymbol{\rm 0}} \hspace{0.05cm}.$$

Note that in these equations $\underline{0}$ denotes a row vector with $k$ elements and $\boldsymbol{\rm 0}$ denotes a matrix with $m$ rows and $k$ columns. All elements of $\underline{0}$ or $\boldsymbol{\rm 0}$ are zero.

If the code is a systematic code, the description variables $\boldsymbol{\rm H}$ and $\boldsymbol{\rm G}$ can be written with the aid of unit (identity) matrices as follows:

$${ \boldsymbol{\rm G}} =\left({ \boldsymbol{\rm I}}_k \: ; \: { \boldsymbol{\rm P}}\right) \hspace{0.5cm} \Rightarrow \hspace{0.5cm} { \boldsymbol{\rm H}} = \left({ \boldsymbol{\rm P}}^{\rm T}\: ; \:{ \boldsymbol{\rm I}}_m \right) \hspace{0.05cm}.$$

$\boldsymbol{\rm P}$ is thereby a matrix with $k$ rows and $m$ columns. Accordingly, the transposed matrix ${ \boldsymbol{\rm P}}^{\rm T}$ consists of $m$ rows and $k$ columns.

Hints :

This exercise belongs to the chapter General Description of Linear Block Codes.
Reference is made in particular to the pages Code definition by the parity-check matrix and Code definition by the generator matrix.

Questions

Solution

(1) The number of columns of the parity-check matrix $\boldsymbol{\rm H}$ is equal to the code length $\underline{n = 7}$.

The number of rows is equal to the number of parity-check equations, in this case $\underline{m = 3} = n - k$.

(2) A comparison with the graph on the information page shows that all statements are true. With

$$\underline{x} = ( x_1, x_2, x_3, x_4, x_5, x_6, x_7) = ( u_1, u_2, u_3, u_4, p_1, p_2, p_3)$$

results in the following parity-check equations:

$$x_1 \oplus x_2 \oplus x_4 \oplus x_5 \hspace{-0.1cm}\ = \ \hspace{-0.1cm} 0 \hspace{0.3cm}{\rm (roter\hspace{0.15cm}Kreis)}\hspace{0.05cm},$$

$$x_2 \oplus x_3 \oplus x_4 \oplus x_6 \hspace{-0.1cm}\ = \ \hspace{-0.1cm} 0 \hspace{0.3cm}{\rm (gr\ddot{u}ner\hspace{0.15cm}Kreis)}\hspace{0.05cm},$$

$$ x_1 \oplus x_3 \oplus x_4 \oplus x_7 \hspace{-0.1cm}\ = \ \hspace{-0.1cm} 0 \hspace{0.3cm}{\rm (blauer\hspace{0.15cm}Kreis)}\hspace{0.05cm}.$$

Damit erhält man für die Prüfmatrix:

$${ \boldsymbol{\rm H}} = \begin{pmatrix} 1 &1 &0 &1 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0\\ 1 &0 &1 &1 &0 &0 &1 \end{pmatrix}\hspace{0.05cm}.$$

Die Angabe von $\boldsymbol{\rm H}$ ist nicht eindeutig. Bei anderer Reihenfolge der Prüfgleichungen ergäbe sich beispielsweise eine zweite, ebenfalls richtige Prüfmatrix:

$${ \boldsymbol{\rm H}}' = \begin{pmatrix} 1 &0 &1 &1 &0 &0 &1\\ 1 &1 &0 &1 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0 \end{pmatrix}\hspace{0.05cm}.$$

(3) Richtig ist die Aussage 2:

Bei einem systematischen Code lässt sich die Prüfmatrix in folgender Form darstellen:

$${ \boldsymbol{\rm H}} =\left({ \boldsymbol{\rm P}}^{\rm T}\: ; \:{ \boldsymbol{\rm I}}_m \right) \hspace{0.05cm}.$$

Im vorliegenden Beispiel gilt mit $m = 3$:

$${ \boldsymbol{\rm P}}^{\rm T} = \begin{pmatrix} 1 &1 &0 &1\\ 0 &1 &1 &1\\ 1 &0 &1 &1 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm I}}_3 = \begin{pmatrix} 1 &0 &0\\ 0 &1 &0\\ 0 &0 &1 \end{pmatrix}\hspace{0.05cm}.$$

(4) Richtig sind die Aussagen 1 und 3:

Allgemein lautet der Zusammenhang zwischen der $m×n$–Prüfmatrix und der $k×n$–Generatormatrix:

$${ \boldsymbol{\rm H}} \cdot { \boldsymbol{\rm G}}^{\rm T} = { \boldsymbol{\rm 0}} \hspace{0.05cm}$$

Die Matrix $ \boldsymbol{\rm 0}$ ist nur mit Nullen belegt und hat $m$ Zeilen und $k$ Spalten. Bei einem systematischen Code – wie hier – besteht folgender Zusammenhang:

$${ \boldsymbol{\rm H}} =\left({ \boldsymbol{\rm P}}^{\rm T}\: ; \:{ \boldsymbol{\rm I}}_m \right) \hspace{0.3cm}\Leftrightarrow \hspace{0.3cm}{ \boldsymbol{\rm G}} =\left({ \boldsymbol{\rm I}}_k \: ; \:{ \boldsymbol{\rm P}} \right) \hspace{0.05cm}.$$

Im vorliegenden Fall erhält man:

$${ \boldsymbol{\rm I}}_4 = \begin{pmatrix} 1 &0 &0 &0\\ 0 &1 &0 &0\\ 0 &0 &1 &0\\ 0 &0 &0 &1 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm P}} = \begin{pmatrix} 1 &0 &1\\ 1 &1 &0\\ 0 &1 &1\\ 1 &1 &1 \end{pmatrix}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} { \boldsymbol{\rm G}} = \begin{pmatrix} 1 &0 &0 &0 &1 &0 &1\\ 0 &1 &0 &0 &1 &1 &0\\ 0 &0 &1 &0 &0 &1 &1\\ 0 &0 &0 &1 &1 &1 &1 \end{pmatrix}\hspace{0.05cm}.$$

(5) Die anzuwendende Gleichung lautet:

$$\underline{x}_{11} \hspace{-0.15cm}\ = \ \hspace{-0.15cm} \underline{u}_{11} \cdot { \boldsymbol{\rm G}} = \begin{pmatrix} 1 &0 &1 &1 \end{pmatrix} \cdot \begin{pmatrix} 1 &0 &0 &0 &1 &0 &1\\ 0 &1 &0 &0 &1 &1 &0\\ 0 &0 &1 &0 &0 &1 &1\\ 0 &0 &0 &1 &1 &1 &1 \end{pmatrix} = \begin{pmatrix} 1 &0 &1 &1 &0 &0 &1 \end{pmatrix}\hspace{0.05cm}.$$

Ein Vergleich mit der Tabelle von Aufgabe 1.6 zeigt die Richtigkeit dieser Berechnung ⇒ Antwort 3.

Die Antwort 1 kann schon deshalb nicht richtig sein, weil das keiner systematischen Codierung entspricht.
(1, 0, 1, 1, 0, 0, 0) gemäß Vorschlag 2 ist kein gültiges Codewort. Hiermit wird die in der Grafik auf der Angabenseite blau markierte Prüfgleichung nicht erfüllt.

	The first row is: $1101100$.
	The second row is: $0111010$.
	The third row is: $1011001$.

	In each row there is an even number of ones.
	At the end of $\boldsymbol{\rm H}$ you can recognize a unit matrix.
	The middle column of $\boldsymbol{\rm H}$ is occupied by ones.

	The first row is: $1000101$,
	The second row is: $0111010$,
	The last row is: $0001111$.

	$x_{11} = (1, 1, 1, 1, 0, 0, 0),$
	$x_{11} = (1, 0, 1, 1, 0, 0, 0),$
	$x_{11} = (1, 0, 1, 1, 0, 0, 1).$