Difference between revisions of "Aufgaben:Exercise 1.12Z: Comparison of HC (7, 4, 3) and HC (8, 4, 4)"
| (48 intermediate revisions by 8 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Decoding_of_Linear_Block_Codes}} |
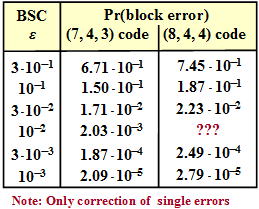
| + | [[File:EN_KC_Z_1_12_neu.png|right|frame|Block error probabilities of $\rm HC \ (7, 4, 3)$ and $\rm HC \ (8, 4, 4)$]] | ||
| − | + | Now the block error probabilities | |
| + | *of the $(7, 4, 3)$ Hamming code and | ||
| + | *of the extended $(8, 4, 4)$ Hamming code | ||
| − | |||
| − | + | are compared with each other. The following are used as a basis: | |
| − | + | *The [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Symmetric_Channel_.E2.80.93_BSC|"BSC channel model"]] $($parameters $\varepsilon$, in particular $\varepsilon = 0.01$ for numerical results$)$, | |
| − | |||
| − | |||
| − | * | ||
| − | |||
| − | + | *the [[Channel_Coding/Decoding_of_Linear_Block_Codes#Principle_of_syndrome_decoding|"syndrome decoding"]], which implements maximum likelihood detection for both codes; correct assignment of the syndrome table yields the minimum block error probability in each case. | |
| − | |||
| − | |||
| − | + | For the $(7, 4, 3)$ Hamming code was calculated in [[Aufgaben:Exercise_1.12:_Hard_Decision_vs._Soft_Decision|"Exercise 1.12"]]: | |
| − | + | :$${\rm Pr(block\:error)} = 1 - (1 - \varepsilon)^7 - 7 \cdot \varepsilon \cdot (1 - \varepsilon)^6 \hspace{0.05cm}.$$ | |
| − | |||
| − | + | The numerical values are given in the second column of the table above. They are the actual values, i.e. not the approximation derived in [[Aufgaben:Exercise_1.12:_Hard_Decision_vs._Soft_Decision|"Exercise 1.12"]]: ${\rm Pr(block\:error)} \approx 21 \cdot \varepsilon^2$. | |
| + | It should be noted that only hard decisions are possible due to the BSC channel model. With [[Channel_Coding/Decoding_of_Linear_Block_Codes#Coding_gain_-_bit_error_rate_with_AWGN|"Soft Decision"]] slightly smaller block error probabilities result. | ||
| − | '' | + | Now the block error probability for the extended $(8, 4, 4)$ code is to be determined: |
| + | *The calculation in subtask '''(4)''' is made with the proviso that, as for the $(7, 4, 3)$ code, only the error patterns with a single "$1$" are corrected. In the right column of the above table, the results are entered, except for the value for $\varepsilon = 0.01$, which is to be calculated explicitly. | ||
| − | + | *In subtask '''(5)''' it is to be taken into account that with the extended $(8, 4, 4)$ code, parts of the syndrome table can still be filled with weight-2 error patterns. | |
| − | |||
| − | { | + | |
| + | Hints: | ||
| + | * This exercise belongs to the chapter [[Channel_Coding/Decoding_of_Linear_Block_Codes|"Decoding of Linear Block Codes"]]. | ||
| + | |||
| + | * Of particular interest for solving this exercise is the section [[Channel_Coding/Decoding_of_Linear_Block_Codes#Generalization_of_syndrome_coding|"Generalization of Syndrome Decoding"]]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
| + | <quiz display=simple> | ||
| + | {How many entries do the respective syndrome tables contain in total? | ||
|type="{}"} | |type="{}"} | ||
| − | $ | + | $(7, 4, 3)\:{\rm code} \text{:} \hspace{0.4cm} N_{\rm ges} \ = \ $ { 8 } |
| − | $ | + | $(8, 4, 4)\:{\rm code} \text{:} \hspace{0.4cm} N_{\rm ges} \ = \ $ { 16 } |
| − | { | + | {How many weight-2 error patterns $(N_2')$ are there in total? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $(7, 4, 3)\:{\rm code} \text{:} \hspace{0.4cm} N_2' \ = \ $ { 21 } |
| − | $ | + | $(8, 4, 4)\:{\rm code} \text{:} \hspace{0.4cm} N_2' \ = \ $ { 28 } |
| + | {How many error patterns in the syndrome tables $(N_2)$ contain two ones? | ||
| + | |type="{}"} | ||
| + | $(7, 4, 3)\:{\rm code} \text{:} \hspace{0.4cm} N_2 \ = \ $ { 0. } | ||
| + | $(8, 4, 4)\:{\rm code} \text{:} \hspace{0.4cm} N_2 \ = \ $ { 7 } | ||
| − | { | + | {Let it now $\varepsilon = 0.01$. What is the block error probability for the extended $(8, 4, 4)$ code <u>without weight-2 error correction</u>? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | ${\rm Pr(block\:error)} \ = \ $ { 2.69 3% } $\ \cdot 10^{-3}$ |
| − | $ | ||
| − | { | + | {In contrast, what result is obtained <u>with weight-2 error correction</u>? |
|type="{}"} | |type="{}"} | ||
| − | $\ {\rm Pr( | + | $\ {\rm Pr(block\:error)} \ = \ $ { 2.03 3% } $\ \cdot 10^{-3}$ |
| + | </quiz> | ||
| + | |||
| + | ===Solution=== | ||
| + | {{ML-Kopf}} | ||
| + | '''(1)''' The size of the syndrome table is generally $N_{\rm ges} = 2^m$, where $m = n - k$ indicates the number of parity bits. | ||
| + | *In the $(7, 4, 3)$ Hamming code, $m = n - k = 3$ ⇒ the length of the table is $N_{\rm ges} =2^3 \ \underline{= 8}.$ | ||
| + | |||
| + | *The syndrome table of the $(8, 4, 4)$ code is twice as large: $N_{\rm ges} = 2^4 \ \underline{= 16}$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' In general, for the number of entries with weight-2 error patterns, $N_2' = $"$n {\rm \ over \ } 2$". This results in the numerical values | ||
| + | *$N_2' \ \underline{= 21} \ $ für $n = 7 \ \ ⇒ \ \ (7, 4, 3)$ code, | ||
| + | *$N_2' \ \underline{= 28} \ $ für $n = 8 \ \ \Rightarrow \ \ (8, 4, 4)$ code. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' In the $\rm HC (7, 4, 3)$, the syndrome table is filled with | ||
| + | :*one entry for the error-free case $(N_{0}= 1)$ | ||
| + | :*and $n = 7$ entries with weight-1 error patterns $(N_{1} = 7)$. | ||
| + | |||
| + | |||
| + | *Thus, the number of entries with weight-2 error patterns is | ||
| + | |||
| + | :$$N_2 = N_{\rm ges} - N_0 - N_1 \hspace{0.15cm} \underline{= 0} \hspace{0.05cm}.$$ | ||
| + | |||
| + | *In contrast, for the extended $(8, 4, 4)$ Hamming code: | ||
| + | :$$N_0 = 1\hspace{0.05cm},\hspace{0.2cm}N_1 = 8 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} N_2 = N_{\rm ges} - N_0 - N_1 \hspace{0.15cm} \underline{= 7} \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| + | '''(4)''' Analogous to the [[Aufgaben:Exercise_1.12:_Hard_Decision_vs._Soft_Decision| "solution"]] of the first two parts of Exercise 1.12, here you get: | ||
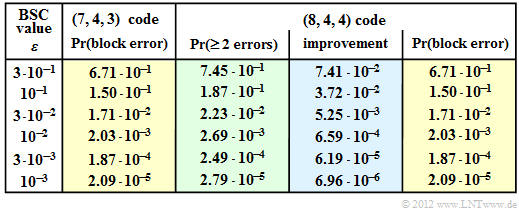
| + | [[File:EN_KC_A_1_12d_neu.png|right|frame|Block error probability of $(7, 4, 3)$ and $(8, 4, 4)$ code]] | ||
| + | :$${\rm Pr(block\:error)} = 1 - (1 - \varepsilon)^8 - 8 \cdot \varepsilon \cdot (1 - \varepsilon)^7$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}{\rm Pr(block\:error)} =1 - 0.922745 - 0.074655\hspace{0.15cm} \underline{= 2.69 \cdot 10^{-3}} \hspace{0.05cm}.$$ | ||
| − | + | *In the table for this case and for different BSC parameters $ε$, the results are entered in the third column ⇒ ${\rm Pr}(\ge \text{2 errors)}$. | |
| + | |||
| + | *Compared to the $(7, 4, 3)$ Hamming code corresponding to the second column, there is always a deterioration. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(5)''' With the best possible correction ("filled syndrome table"), seven weight-2 error patterns are also corrected. | ||
| + | *This reduces the block error probability by the "improvement" (column 4): | ||
| + | |||
| + | :$${\rm Pr(corrected\hspace{0.15cm}weight\hspace{-0.1cm}-\hspace{-0.1cm}2\hspace{0.15cm}error\hspace{0.15cm} pattern)} = 7 \cdot \varepsilon^2 \cdot (1 - \varepsilon)^6 \hspace{0.05cm}.$$ | ||
| + | *For $\varepsilon = 0.01$, this "improvement" accounts for about $6.59\cdot10^{-4}$. | ||
| + | |||
| + | *The block error probability of the $(8, 4, 4)$ code (last column) is thus given by | ||
| − | + | :$${\rm Pr(block\:error)} = 2.69 \cdot 10^{-3} - 0.66 \cdot 10^{-3} \underline{= 2.03 \cdot 10^{-3}} \hspace{0.05cm}.$$ | |
| + | |||
| + | In the table above, this calculation is performed for different BSC parameters $\varepsilon$. One can see: | ||
| + | #The block error probability of the $(8, 4, 4)$ extended Hamming code (last column) exactly matches that of the $(7, 4, 3)$ Hamming code (column 2). | ||
| + | #The $25\%$ correction to the weight-2 error patterns exactly balances the fact that error patterns with more than one error (column 3) are more likely for the $(8, 4, 4)$ code than for the $(7, 4, 3)$ code (column 2). | ||
| + | {{ML-Fuß}} | ||
| − | ^]] | + | [[Category:Channel Coding: Exercises|^1.5 Linear Block Code Decoding^]] |
Latest revision as of 12:30, 5 April 2023
Now the block error probabilities
- of the $(7, 4, 3)$ Hamming code and
- of the extended $(8, 4, 4)$ Hamming code
are compared with each other. The following are used as a basis:
- The "BSC channel model" $($parameters $\varepsilon$, in particular $\varepsilon = 0.01$ for numerical results$)$,
- the "syndrome decoding", which implements maximum likelihood detection for both codes; correct assignment of the syndrome table yields the minimum block error probability in each case.
For the $(7, 4, 3)$ Hamming code was calculated in "Exercise 1.12":
- $${\rm Pr(block\:error)} = 1 - (1 - \varepsilon)^7 - 7 \cdot \varepsilon \cdot (1 - \varepsilon)^6 \hspace{0.05cm}.$$
The numerical values are given in the second column of the table above. They are the actual values, i.e. not the approximation derived in "Exercise 1.12": ${\rm Pr(block\:error)} \approx 21 \cdot \varepsilon^2$.
It should be noted that only hard decisions are possible due to the BSC channel model. With "Soft Decision" slightly smaller block error probabilities result.
Now the block error probability for the extended $(8, 4, 4)$ code is to be determined:
- The calculation in subtask (4) is made with the proviso that, as for the $(7, 4, 3)$ code, only the error patterns with a single "$1$" are corrected. In the right column of the above table, the results are entered, except for the value for $\varepsilon = 0.01$, which is to be calculated explicitly.
- In subtask (5) it is to be taken into account that with the extended $(8, 4, 4)$ code, parts of the syndrome table can still be filled with weight-2 error patterns.
Hints:
- This exercise belongs to the chapter "Decoding of Linear Block Codes".
- Of particular interest for solving this exercise is the section "Generalization of Syndrome Decoding".
Questions
Solution
- In the $(7, 4, 3)$ Hamming code, $m = n - k = 3$ ⇒ the length of the table is $N_{\rm ges} =2^3 \ \underline{= 8}.$
- The syndrome table of the $(8, 4, 4)$ code is twice as large: $N_{\rm ges} = 2^4 \ \underline{= 16}$.
(2) In general, for the number of entries with weight-2 error patterns, $N_2' = $"$n {\rm \ over \ } 2$". This results in the numerical values
- $N_2' \ \underline{= 21} \ $ für $n = 7 \ \ ⇒ \ \ (7, 4, 3)$ code,
- $N_2' \ \underline{= 28} \ $ für $n = 8 \ \ \Rightarrow \ \ (8, 4, 4)$ code.
(3) In the $\rm HC (7, 4, 3)$, the syndrome table is filled with
- one entry for the error-free case $(N_{0}= 1)$
- and $n = 7$ entries with weight-1 error patterns $(N_{1} = 7)$.
- Thus, the number of entries with weight-2 error patterns is
- $$N_2 = N_{\rm ges} - N_0 - N_1 \hspace{0.15cm} \underline{= 0} \hspace{0.05cm}.$$
- In contrast, for the extended $(8, 4, 4)$ Hamming code:
- $$N_0 = 1\hspace{0.05cm},\hspace{0.2cm}N_1 = 8 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} N_2 = N_{\rm ges} - N_0 - N_1 \hspace{0.15cm} \underline{= 7} \hspace{0.05cm}.$$
(4) Analogous to the "solution" of the first two parts of Exercise 1.12, here you get:
- $${\rm Pr(block\:error)} = 1 - (1 - \varepsilon)^8 - 8 \cdot \varepsilon \cdot (1 - \varepsilon)^7$$
- $$\Rightarrow \hspace{0.3cm}{\rm Pr(block\:error)} =1 - 0.922745 - 0.074655\hspace{0.15cm} \underline{= 2.69 \cdot 10^{-3}} \hspace{0.05cm}.$$
- In the table for this case and for different BSC parameters $ε$, the results are entered in the third column ⇒ ${\rm Pr}(\ge \text{2 errors)}$.
- Compared to the $(7, 4, 3)$ Hamming code corresponding to the second column, there is always a deterioration.
(5) With the best possible correction ("filled syndrome table"), seven weight-2 error patterns are also corrected.
- This reduces the block error probability by the "improvement" (column 4):
- $${\rm Pr(corrected\hspace{0.15cm}weight\hspace{-0.1cm}-\hspace{-0.1cm}2\hspace{0.15cm}error\hspace{0.15cm} pattern)} = 7 \cdot \varepsilon^2 \cdot (1 - \varepsilon)^6 \hspace{0.05cm}.$$
- For $\varepsilon = 0.01$, this "improvement" accounts for about $6.59\cdot10^{-4}$.
- The block error probability of the $(8, 4, 4)$ code (last column) is thus given by
- $${\rm Pr(block\:error)} = 2.69 \cdot 10^{-3} - 0.66 \cdot 10^{-3} \underline{= 2.03 \cdot 10^{-3}} \hspace{0.05cm}.$$
In the table above, this calculation is performed for different BSC parameters $\varepsilon$. One can see:
- The block error probability of the $(8, 4, 4)$ extended Hamming code (last column) exactly matches that of the $(7, 4, 3)$ Hamming code (column 2).
- The $25\%$ correction to the weight-2 error patterns exactly balances the fact that error patterns with more than one error (column 3) are more likely for the $(8, 4, 4)$ code than for the $(7, 4, 3)$ code (column 2).