Difference between revisions of "Aufgaben:Exercise 1.14: Bhattacharyya Bound for BEC"
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Limits_for_Block_Error_Probability}} |
[[File:P_ID2411__KC_A_1_13.png|right|frame|Possible received vectors for the $(5, 2)$ code and BEC]] | [[File:P_ID2411__KC_A_1_13.png|right|frame|Possible received vectors for the $(5, 2)$ code and BEC]] | ||
| Line 39: | Line 39: | ||
| − | + | Computing the block error probability is difficult because the events $[\underline{x}_{0} → \underline{x}_{1}]$ , $[\underline{x}_{0} → \underline{x}_{2}]$ and $[\underline{x}_{0} → \underline{x}_{3}]$ are not necessarily [[Theory_of_Stochastic_Signals/Set_Theory_Basics#Disjoint_sets|disjoint]] . An upper bound is provided by [[Channel_Coding/Limits_for_Block_Error_Probability#Union_Bound_of_the_block_error_probability|Union Bound]]: | |
:$${\rm Pr(Union \hspace{0.15cm}Bound)} = {\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}2}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}3}] \ge {\rm Pr(Blockfehler)} \hspace{0.05cm}.$$ | :$${\rm Pr(Union \hspace{0.15cm}Bound)} = {\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}2}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}3}] \ge {\rm Pr(Blockfehler)} \hspace{0.05cm}.$$ | ||
| − | + | ||
| + | Another bound was given by Bhattacharyya: | ||
| − | :$${\rm Pr(Bhattacharyya)} = W(\beta)-1 \ge {\rm Pr(Union \hspace{0.15cm}Bound)} \ge {\rm Pr( | + | :$${\rm Pr(Bhattacharyya)} = W(\beta)-1 \ge {\rm Pr(Union \hspace{0.15cm}Bound)} \ge {\rm Pr(block\:error)} \hspace{0.05cm},$$ |
| − | + | where, for the Binary Erasure Channel, Bhattacharyya parameter $\beta = \lambda$ and $W(X)$ the [[Channel_Coding/Limits_for_Block_Error_Probability#Distance_spectrum_of_a_linear_code|weight enumerator function]] where the pseudo-variable $X$ is to be replaced here by the Bhattacharyya parameter $\lambda$ . | |
| − | * | + | *The Bhattacharyya bound is more or less far above the ''Union Bound.'' depending on the channel. |
| − | * | + | *Its importance lies in the fact that the bound can be specified in the same way for different channels. |
| Line 58: | Line 59: | ||
| − | + | Hints: | |
| − | * | + | *The exercise belongs to the chapter [[Channel_Coding/Limits_for_Block_Error_Probability|Bounds on block error probability]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the pairwise error probability between the codewords $\underline{x}_{0} = (0, 0, 0, 0, 0)$ and $\underline{x}_{1} = (0, 1, 0, 1, 1)$? |
|type="{}"} | |type="{}"} | ||
${\rm Pr}[\underline{x}_{0} → \underline{x}_{1}] \ = \ $ { 0.5 3% }$\ \cdot 10^{-3} $ | ${\rm Pr}[\underline{x}_{0} → \underline{x}_{1}] \ = \ $ { 0.5 3% }$\ \cdot 10^{-3} $ | ||
| − | { | + | {Which statements are true regarding ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}]$ with index $i = 1, \ \text{...} \ , 3$? <br>$d_{{\rm H},\hspace{0.05cm}i}$ bezeichnet hier die Hamming–Distanz zwischen $x_{0}$ und $x_{i}$. |
|type="()"} | |type="()"} | ||
| − | - | + | - It holds ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}] \ = \ \lambda ^{d_{{\rm H},\hspace{0.05cm}i}} \ · \ (1 – \lambda)^{n \hspace{0.05cm}– \hspace{0.05cm}d_{{\rm H},\hspace{0.05cm}i}}$. |
| − | + | + | + It holds ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}] \ = \ 1/2 · \lambda ^{d_{{\rm H},\hspace{0.05cm}i}}.$ |
| − | - ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}]$ | + | - ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}]$ is the corruption probability of $x_{0}$ nach $x_{i}$. |
| − | { | + | {What are the following probabilities? |
|type="{}"} | |type="{}"} | ||
$\ {\rm Pr}[\underline{x}_{0} → \underline{x}_{2}] \ = \ $ { 0.5 3% } $\ \cdot 10^{-3} $ | $\ {\rm Pr}[\underline{x}_{0} → \underline{x}_{2}] \ = \ $ { 0.5 3% } $\ \cdot 10^{-3} $ | ||
$\ {\rm Pr}[\underline{x}_{0} → \underline{x}_{3}] \ = \ $ { 0.05 3% } $\ \cdot 10^{-3} $ | $\ {\rm Pr}[\underline{x}_{0} → \underline{x}_{3}] \ = \ $ { 0.05 3% } $\ \cdot 10^{-3} $ | ||
| − | { | + | {Specify the ''Union Bound'' for the block error probability. |
|type="{}"} | |type="{}"} | ||
$\ {\rm Pr(Union\ Bound)} \ = \ ${ 1.05 3% } $\ \cdot 10^{-3} $ | $\ {\rm Pr(Union\ Bound)} \ = \ ${ 1.05 3% } $\ \cdot 10^{-3} $ | ||
| − | { | + | {What is the ''Bhattacharyya bound'' in the present case? |
|type="{}"} | |type="{}"} | ||
$\ {\rm Pr(Bhattacharyya)} \ = \ ${ 2.1 3% } $\ \cdot 10^{-3} $ | $\ {\rm Pr(Bhattacharyya)} \ = \ ${ 2.1 3% } $\ \cdot 10^{-3} $ | ||
| Line 92: | Line 93: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
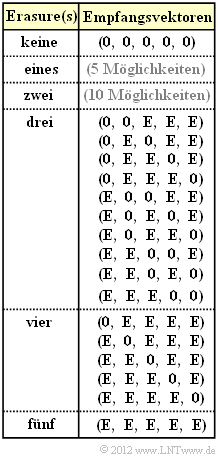
'''(1)''' Die Codeworte $\underline{x}_{0}$ und $\underline{x}_{1}$ unterscheiden sich in Bit $2, \ 4$ und $5$. Wird nur einer dieser drei Binärwerte richtig übertragen, ist damit das gesamte Codewort eindeutig bestimmt. Keine Information über das Codewort erhält man bei folgenden Empfangsvektoren (siehe Tabelle auf der Angabenseite): | '''(1)''' Die Codeworte $\underline{x}_{0}$ und $\underline{x}_{1}$ unterscheiden sich in Bit $2, \ 4$ und $5$. Wird nur einer dieser drei Binärwerte richtig übertragen, ist damit das gesamte Codewort eindeutig bestimmt. Keine Information über das Codewort erhält man bei folgenden Empfangsvektoren (siehe Tabelle auf der Angabenseite): | ||
Revision as of 22:57, 28 July 2022
In this exercise, we consider the systematic $(5, 2)$ code
- with the $2×5$ generator matrix
- $${ \boldsymbol{\rm G}}_{(5, 2)} = \begin{pmatrix} 1 &0 &1 &1 &0\\ 0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm},$$
- the $3 × 5$ parity-check matrix
- $${ \boldsymbol{\rm H}}_{(5, 2)} = \begin{pmatrix} 1 &0 &1 &0 &0\\ 1 &1 &0 &1 &0\\ 0 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm},$$
- and the $2^k = 4$ code words
- $$\underline{x}_0 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.2cm}\underline{x}_1 = (0, 1, 0, 1, 1)\hspace{0.05cm},\hspace{0.2cm}\underline{x}_2 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} (1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.2cm}\underline{x}_3 = (1, 1, 1, 0, 1)\hspace{0.05cm}.$$
At the output of the digital channel defined by the BEC model (Binary Erasure Channel) with the erasure probability $\lambda = 0.001$ the received vector
- $$\underline{y} = (y_1, \hspace{0.05cm}y_2, \hspace{0.05cm}y_3, \hspace{0.05cm}y_4, \hspace{0.05cm}y_5)$$
occurs, where for $i = 1, \ \text{...} \ , 5$ holds: $y_{i} \in \{0, 1, \rm E\}$.
The BEC channel is characterized by the fact that.
- corruptions $(0 → 1, 1 → 0)$ are excluded,
- but cancellations $(0 → \rm E, 1 → E)$ may occur.
The graph explicitly shows all possible received vectors $\underline{y}$ with three or more erasures $\rm E$ assuming that the all-zero vector $(0, 0, 0, 0, 0)$ was sent.
- For less than three extinctions, for the considered $(5, 2)$ code, the codeword finder always returns the correct decision: $\underline{z} = \underline{x}$.
- On the other hand, if there are three or more erasures, wrong decisions may occur. In this case, the following applies to the block error probability:
- $$ {\rm Pr(block\:error)}= {\rm Pr} (\underline{z} \ne \underline{x}) = {\rm Pr}\left \{ \hspace{0.1cm} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] \hspace{0.05cm}\cup\hspace{0.05cm}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}] \hspace{0.05cm}\cup \hspace{0.05cm}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}] \hspace{0.1cm}\right \} \hspace{0.05cm}.$$
Please note:
- The event $[\underline{x}_{0} → \underline{x}_{1}]$ does not necessarily say that at the received vector under consideration $\underline{y}$ is actually decided for the codeword $\underline{x}_{1}$ is decided, but only that the decision for $x_{1}$ would be more reasonable than the decision for $\underline{x}_{0}$ due to statistics.
- But it could also be decided for $\underline{x}_{2}$ or $\underline{x}_{3}$ if the maximum-likelihood criterion is in favor.
Computing the block error probability is difficult because the events $[\underline{x}_{0} → \underline{x}_{1}]$ , $[\underline{x}_{0} → \underline{x}_{2}]$ and $[\underline{x}_{0} → \underline{x}_{3}]$ are not necessarily disjoint . An upper bound is provided by Union Bound:
- $${\rm Pr(Union \hspace{0.15cm}Bound)} = {\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}2}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}3}] \ge {\rm Pr(Blockfehler)} \hspace{0.05cm}.$$
Another bound was given by Bhattacharyya:
- $${\rm Pr(Bhattacharyya)} = W(\beta)-1 \ge {\rm Pr(Union \hspace{0.15cm}Bound)} \ge {\rm Pr(block\:error)} \hspace{0.05cm},$$
where, for the Binary Erasure Channel, Bhattacharyya parameter $\beta = \lambda$ and $W(X)$ the weight enumerator function where the pseudo-variable $X$ is to be replaced here by the Bhattacharyya parameter $\lambda$ .
- The Bhattacharyya bound is more or less far above the Union Bound. depending on the channel.
- Its importance lies in the fact that the bound can be specified in the same way for different channels.
Hints:
- The exercise belongs to the chapter Bounds on block error probability.
Questions
Solution
- $\underline{y} = (0, {\rm E}, 0, {\rm E}, {\rm E})$ mit Wahrscheinlichkeit $\lambda^3 \ · \ (1 – \lambda)^2$,
- $\underline{y} = (0, {\rm E}, {\rm E}, {\rm E}, {\rm E})$ mit Wahrscheinlichkeit $\lambda^4 \ · \ (1 – \lambda)$,
- $\underline{y} = ({\rm E}, {\rm E}, 0, {\rm E}, {\rm E})$ mit Wahrscheinlichkeit $\lambda^4 \ · \ (1 – \lambda)$,
- $\underline{y} = ({\rm E}, {\rm E}, {\rm E}, {\rm E}, {\rm E})$ mit Wahrscheinlichkeit $\lambda^5$.
Die Wahrscheinlichkeit, dass aufgrund des spezifischen Empfangsvektors $\underline{y}$ das Codewort $\underline{x}_{1}$ genau so wahrscheinlich ist wie $\underline{x}_{0}$, ergibt sich zu
- $$\ {\rm Pr}\ [\underline{x}_0 \hspace{0.12cm}{\rm und}\hspace{0.12cm} \underline{x}_1 \hspace{0.15cm}{\rm sind \hspace{0.15cm}gleichwahrscheinlich}] = \lambda^3 \cdot (1- \lambda)^2 + 2 \cdot \lambda^4 \cdot (1- \lambda) + \lambda^5 =\lambda^3 \cdot \left [ (1- \lambda)^2 + 2 \cdot \lambda \cdot (1- \lambda) + \lambda^2 \right ] = \lambda^3 \hspace{0.05cm}.$$
In diesem Fall entscheidet man sich nach dem Zufallsprinzip für $\underline{x}_{0}$ (wäre richtig) oder für $\underline{x}_{1}$ (leider falsch), und zwar mit gleicher Wahrscheinlichkeit. Daraus folgt:
- $${\rm Pr} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] = 1/2 \cdot \lambda^3 \hspace{0.15cm} \underline{= 0.5 \cdot 10^{-3}} \hspace{0.05cm}.$$
(2) Nach Teilaufgabe (1) ist die Antwort 2 richtig und nicht die Antwort 1. Auch die Aussage 3 ist falsch:
- ${\rm Pr}[\underline{x}_{0} → \underline{x}_{1}]$ sagt nicht aus, dass mit dieser Wahrscheinlickeit das Codewort $\underline{x}_{0}$ tatsächlich in das falsche Codewort $\underline{x}_{1}$ übergeht, sondern nur, dass es mit dieser Wahrscheinlichkeit zu $\underline{x}_{1}$ übergehen könnte.
- ${\rm Pr}[\underline{x}_{0} → \underline{x}_{1}]$ beinhaltet auch Konstellationen, bei denen die Entscheidung tatsächlich für $\underline{x}_{2}$ bzw. $\underline{x}_{3}$ fällt.
(3) Wegen $d_{\rm H}(\underline{x}_{0}, \underline{x}_{2}) = 3$ und $d_{\rm H}(\underline{x}_{0}, \underline{x}_{3}) = 4$ ergibt sich hierfür
- $${\rm Pr} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}] = 1/2 \cdot \lambda^3 \hspace{0.15cm} \underline{= 0.5 \cdot 10^{-3}} \hspace{0.05cm},\hspace{0.2cm} {\rm Pr} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}] = 1/2 \cdot \lambda^4 \hspace{0.15cm} \underline{= 0.05 \cdot 10^{-3}} \hspace{0.05cm}.$$
(4) Die Blockfehlerwahrscheinlichkeit ist nie größer (mit einer gewissen Wahrscheinlichkeit eher kleiner) als die so genannte Union Bound:
- $${\rm Pr(Union \hspace{0.15cm}Bound)} \hspace{-0.15cm}\ = \ \hspace{-0.15cm} {\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}2}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}3}] = 2 \cdot \lambda^3/2 + \lambda^4/2 = 0.001 + 0.00005 \hspace{0.15cm} \underline{= 1.05 \cdot 10^{-3}} \hspace{0.05cm}.$$
(5) Allgemein gilt:
- $${\rm Pr(Blockfehler) ≤ {\rm Pr(Union \hspace{0.15cm}Bound)} \le Pr(Bhattacharyya)} = W(\beta) - 1.$$
- Für das Distanzspektrum bzw. die Gewichtsfunktion erhält man im vorliegenden Fall:
- $$W_0 = 1 \hspace{0.05cm}, \hspace{0.2cm} W_3 = 2 \hspace{0.05cm}, \hspace{0.2cm}W_4 = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} W(X) = 1+ 2 \cdot X^{3} +X^{4} \hspace{0.05cm}.$$
- Beim BEC–Kanal gilt zudem $\beta = \lambda$. Daraus folgt als Endergebnis für $\lambda = 0.001$:
- $${\rm Pr(Bhattacharyya)} = 2 \cdot \lambda^3 + \lambda^4 \hspace{0.15cm} \underline{= 2.1 \cdot 10^{-3}} \hspace{0.05cm}.$$
Anzumerken ist, dass beim BEC–Modell die Bhattacharyya–Schranke stets doppelt so groß ist wie die Union Bound, die ja selbst wieder eine obere Schranke für die Blockfehlerwahrscheinlichkeit darstellt.