Difference between revisions of "Aufgaben:Exercise 1.14: Bhattacharyya Bound for BEC"
| Line 1: | Line 1: | ||
{{quiz-Header|Buchseite=Channel_Coding/Limits_for_Block_Error_Probability}} | {{quiz-Header|Buchseite=Channel_Coding/Limits_for_Block_Error_Probability}} | ||
| − | [[File:P_ID2411__KC_A_1_13.png|right|frame|Possible received vectors for the $(5, 2)$ code and BEC]] | + | [[File:P_ID2411__KC_A_1_13.png|right|frame|Possible received vectors for the $(5, 2)$ code and BEC '''Korrektur''']] |
| − | In this exercise, we consider the systematic $(5, 2)$ code | + | In this exercise, we consider the systematic $(5, 2)$ code |
*with the $2×5$ generator matrix | *with the $2×5$ generator matrix | ||
| Line 16: | Line 16: | ||
:$$\underline{x}_0 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.2cm}\underline{x}_1 = (0, 1, 0, 1, 1)\hspace{0.05cm},\hspace{0.2cm}\underline{x}_2 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} (1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.2cm}\underline{x}_3 = (1, 1, 1, 0, 1)\hspace{0.05cm}.$$ | :$$\underline{x}_0 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.2cm}\underline{x}_1 = (0, 1, 0, 1, 1)\hspace{0.05cm},\hspace{0.2cm}\underline{x}_2 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} (1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.2cm}\underline{x}_3 = (1, 1, 1, 0, 1)\hspace{0.05cm}.$$ | ||
| − | At the output of the digital channel defined by the [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Erasure_Channel_.E2.80.93_BEC|"BEC model"]] ( | + | At the output of the digital channel defined by the [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Erasure_Channel_.E2.80.93_BEC|"BEC model"]] ("Binary Erasure Channel") with the erasure probability $\lambda = 0.001$, the received vector |
:$$\underline{y} = (y_1, \hspace{0.05cm}y_2, \hspace{0.05cm}y_3, \hspace{0.05cm}y_4, \hspace{0.05cm}y_5)$$ | :$$\underline{y} = (y_1, \hspace{0.05cm}y_2, \hspace{0.05cm}y_3, \hspace{0.05cm}y_4, \hspace{0.05cm}y_5)$$ | ||
| − | occurs, where for $i = 1, \ \text{...} \ , 5$ holds: $y_{i} \in \{0, 1, \rm E\}$ | + | occurs, where for $i = 1, \ \text{...} \ , 5$ holds: |
| + | :$$y_{i} \in \{0, 1, \rm E\}.$$ | ||
| − | The BEC channel is characterized by the fact that | + | The BEC channel is characterized by the fact that |
| − | * | + | *falsifications $(0 → 1,\ 1 → 0)$ are excluded, |
| − | |||
| − | + | *but erasures $(0 → \rm E,\ 1 → E)$ may occur. | |
| − | |||
| − | *On the other hand, if there are three or more erasures, wrong decisions may occur. In this case, the following applies to the block error probability: | + | |
| + | The graph explicitly shows all possible received vectors $\underline{y}$ with three or more erasures $\rm (E)$ assuming that the all-zero vector $(0, 0, 0, 0, 0)$ was sent. | ||
| + | *For less than three erausures, for the considered $(5, 2)$ code, the "code word finder" always returns the correct decision: $\underline{z} = \underline{x}$. | ||
| + | |||
| + | *On the other hand, if there are three or more erasures, wrong decisions may occur. In this case, the following applies to the block error probability: | ||
:$$ {\rm Pr(block\:error)}= {\rm Pr} (\underline{z} \ne \underline{x}) = {\rm Pr}\left \{ \hspace{0.1cm} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] \hspace{0.05cm}\cup\hspace{0.05cm}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}] \hspace{0.05cm}\cup \hspace{0.05cm}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}] \hspace{0.1cm}\right \} \hspace{0.05cm}.$$ | :$$ {\rm Pr(block\:error)}= {\rm Pr} (\underline{z} \ne \underline{x}) = {\rm Pr}\left \{ \hspace{0.1cm} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] \hspace{0.05cm}\cup\hspace{0.05cm}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}] \hspace{0.05cm}\cup \hspace{0.05cm}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}] \hspace{0.1cm}\right \} \hspace{0.05cm}.$$ | ||
| Line 35: | Line 38: | ||
Please note: | Please note: | ||
| − | *The event $[\underline{x}_{0} → \underline{x}_{1}]$ does not necessarily say that at the received vector under consideration $\underline{y}$ is actually decided for the codeword $\underline{x}_{1}$ | + | *The event $[\underline{x}_{0} → \underline{x}_{1}]$ does not necessarily say that at the received vector under consideration $\underline{y}$ is actually decided for the codeword $\underline{x}_{1}$, but only that the decision for $x_{1}$ would be more reasonable than the decision for $\underline{x}_{0}$ due to statistics. |
| + | |||
*But it could also be decided for $\underline{x}_{2}$ or $\underline{x}_{3}$ if the [[Channel_Coding/Channel_Models_and_Decision_Structures#Criteria_. C2.BBMaximum-a-posteriori.C2.AB_and_.C2.BBMaximum-likelihood.C2.AB|"maximum-likelihood criterion"]] is in favor. | *But it could also be decided for $\underline{x}_{2}$ or $\underline{x}_{3}$ if the [[Channel_Coding/Channel_Models_and_Decision_Structures#Criteria_. C2.BBMaximum-a-posteriori.C2.AB_and_.C2.BBMaximum-likelihood.C2.AB|"maximum-likelihood criterion"]] is in favor. | ||
| − | Computing the block error probability is difficult because the events $[\underline{x}_{0} → \underline{x}_{1}]$ , $[\underline{x}_{0} → \underline{x}_{2}]$ and $[\underline{x}_{0} → \underline{x}_{3}]$ are not necessarily [[Theory_of_Stochastic_Signals/Set_Theory_Basics#Disjoint_sets|"disjoint"]] . An upper bound is provided by [[Channel_Coding/Limits_for_Block_Error_Probability#Union_Bound_of_the_block_error_probability|"Union Bound"]]: | + | Computing the block error probability is difficult because the events $[\underline{x}_{0} → \underline{x}_{1}]$ , $[\underline{x}_{0} → \underline{x}_{2}]$ and $[\underline{x}_{0} → \underline{x}_{3}]$ are not necessarily [[Theory_of_Stochastic_Signals/Set_Theory_Basics#Disjoint_sets|"disjoint"]] . An upper bound is provided by the [[Channel_Coding/Limits_for_Block_Error_Probability#Union_Bound_of_the_block_error_probability|"Union Bound"]]: |
| − | :$${\rm Pr(Union \hspace{0.15cm}Bound)} = {\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}2}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}3}] \ge {\rm Pr( | + | :$${\rm Pr(Union \hspace{0.15cm}Bound)} = {\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}2}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}3}] \ge {\rm Pr(block\hspace{0.15cm}error)} \hspace{0.05cm}.$$ |
| − | + | ||
| − | |||
Another bound was given by Bhattacharyya: | Another bound was given by Bhattacharyya: | ||
:$${\rm Pr(Bhattacharyya)} = W(\beta)-1 \ge {\rm Pr(Union \hspace{0.15cm}Bound)} \ge {\rm Pr(block\:error)} \hspace{0.05cm},$$ | :$${\rm Pr(Bhattacharyya)} = W(\beta)-1 \ge {\rm Pr(Union \hspace{0.15cm}Bound)} \ge {\rm Pr(block\:error)} \hspace{0.05cm},$$ | ||
| − | where | + | where for the binary erasure channel, the Bhattacharyya parameter $\beta = \lambda$ and the [[Channel_Coding/Limits_for_Block_Error_Probability#Distance_spectrum_of_a_linear_code|"weight enumerator function"]] $W(X)$ where the pseudo-variable $X$ is to be replaced here by the Bhattacharyya parameter $\lambda$. |
| − | *The Bhattacharyya | + | *The "Bhattacharyya Bound" is more or less far above the "Union Bound" depending on the channel. |
| + | |||
*Its importance lies in the fact that the bound can be specified in the same way for different channels. | *Its importance lies in the fact that the bound can be specified in the same way for different channels. | ||
| Line 57: | Line 61: | ||
| − | + | Hints: The exercise belongs to the chapter [[Channel_Coding/Limits_for_Block_Error_Probability|"Bounds on block error probability"]]. | |
| − | |||
| − | Hints: | ||
| − | |||
| Line 67: | Line 68: | ||
===Questions=== | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {What is the pairwise error probability between the | + | {What is the pairwise error probability between the code words $\underline{x}_{0} = (0, 0, 0, 0, 0)$ and $\underline{x}_{1} = (0, 1, 0, 1, 1)$? |
|type="{}"} | |type="{}"} | ||
${\rm Pr}[\underline{x}_{0} → \underline{x}_{1}] \ = \ $ { 0.5 3% }$\ \cdot 10^{-3} $ | ${\rm Pr}[\underline{x}_{0} → \underline{x}_{1}] \ = \ $ { 0.5 3% }$\ \cdot 10^{-3} $ | ||
| − | {Which statements are true regarding ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}]$ with index $i = 1, \ \text{...} \ , 3$? | + | {Which statements are true regarding ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}]$ with index $i = 1, \ \text{...} \ , 3$? $d_{{\rm H},\hspace{0.05cm}i}$ denotes here the Hamming distance between $x_{0}$ and $x_{i}$. |
|type="()"} | |type="()"} | ||
- It holds ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}] \ = \ \lambda ^{d_{{\rm H},\hspace{0.05cm}i}} \ · \ (1 – \lambda)^{n \hspace{0.05cm}– \hspace{0.05cm}d_{{\rm H},\hspace{0.05cm}i}}$. | - It holds ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}] \ = \ \lambda ^{d_{{\rm H},\hspace{0.05cm}i}} \ · \ (1 – \lambda)^{n \hspace{0.05cm}– \hspace{0.05cm}d_{{\rm H},\hspace{0.05cm}i}}$. | ||
+ It holds ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}] \ = \ 1/2 · \lambda ^{d_{{\rm H},\hspace{0.05cm}i}}.$ | + It holds ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}] \ = \ 1/2 · \lambda ^{d_{{\rm H},\hspace{0.05cm}i}}.$ | ||
| − | - ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}]$ is the | + | - ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}]$ is the falsification probability from $x_{0}$ to $x_{i}$. |
{What are the following probabilities? | {What are the following probabilities? | ||
| Line 83: | Line 84: | ||
$\ {\rm Pr}[\underline{x}_{0} → \underline{x}_{3}] \ = \ $ { 0.05 3% } $\ \cdot 10^{-3} $ | $\ {\rm Pr}[\underline{x}_{0} → \underline{x}_{3}] \ = \ $ { 0.05 3% } $\ \cdot 10^{-3} $ | ||
| − | {Specify the | + | {Specify the "Union Bound" for the block error probability. |
|type="{}"} | |type="{}"} | ||
$\ {\rm Pr(Union\ Bound)} \ = \ ${ 1.05 3% } $\ \cdot 10^{-3} $ | $\ {\rm Pr(Union\ Bound)} \ = \ ${ 1.05 3% } $\ \cdot 10^{-3} $ | ||
| − | {What is the | + | {What is the "Bhattacharyya Bound" in the present case? |
|type="{}"} | |type="{}"} | ||
$\ {\rm Pr(Bhattacharyya)} \ = \ ${ 2.1 3% } $\ \cdot 10^{-3} $ | $\ {\rm Pr(Bhattacharyya)} \ = \ ${ 2.1 3% } $\ \cdot 10^{-3} $ | ||
Revision as of 16:26, 4 August 2022
In this exercise, we consider the systematic $(5, 2)$ code
- with the $2×5$ generator matrix
- $${ \boldsymbol{\rm G}}_{(5, 2)} = \begin{pmatrix} 1 &0 &1 &1 &0\\ 0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm},$$
- the $3 × 5$ parity-check matrix
- $${ \boldsymbol{\rm H}}_{(5, 2)} = \begin{pmatrix} 1 &0 &1 &0 &0\\ 1 &1 &0 &1 &0\\ 0 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm},$$
- and the $2^k = 4$ code words
- $$\underline{x}_0 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.2cm}\underline{x}_1 = (0, 1, 0, 1, 1)\hspace{0.05cm},\hspace{0.2cm}\underline{x}_2 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} (1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.2cm}\underline{x}_3 = (1, 1, 1, 0, 1)\hspace{0.05cm}.$$
At the output of the digital channel defined by the "BEC model" ("Binary Erasure Channel") with the erasure probability $\lambda = 0.001$, the received vector
- $$\underline{y} = (y_1, \hspace{0.05cm}y_2, \hspace{0.05cm}y_3, \hspace{0.05cm}y_4, \hspace{0.05cm}y_5)$$
occurs, where for $i = 1, \ \text{...} \ , 5$ holds:
- $$y_{i} \in \{0, 1, \rm E\}.$$
The BEC channel is characterized by the fact that
- falsifications $(0 → 1,\ 1 → 0)$ are excluded,
- but erasures $(0 → \rm E,\ 1 → E)$ may occur.
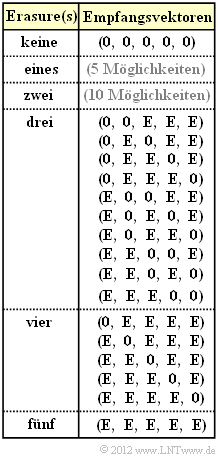
The graph explicitly shows all possible received vectors $\underline{y}$ with three or more erasures $\rm (E)$ assuming that the all-zero vector $(0, 0, 0, 0, 0)$ was sent.
- For less than three erausures, for the considered $(5, 2)$ code, the "code word finder" always returns the correct decision: $\underline{z} = \underline{x}$.
- On the other hand, if there are three or more erasures, wrong decisions may occur. In this case, the following applies to the block error probability:
- $$ {\rm Pr(block\:error)}= {\rm Pr} (\underline{z} \ne \underline{x}) = {\rm Pr}\left \{ \hspace{0.1cm} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] \hspace{0.05cm}\cup\hspace{0.05cm}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}] \hspace{0.05cm}\cup \hspace{0.05cm}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}] \hspace{0.1cm}\right \} \hspace{0.05cm}.$$
Please note:
- The event $[\underline{x}_{0} → \underline{x}_{1}]$ does not necessarily say that at the received vector under consideration $\underline{y}$ is actually decided for the codeword $\underline{x}_{1}$, but only that the decision for $x_{1}$ would be more reasonable than the decision for $\underline{x}_{0}$ due to statistics.
- But it could also be decided for $\underline{x}_{2}$ or $\underline{x}_{3}$ if the "maximum-likelihood criterion" is in favor.
Computing the block error probability is difficult because the events $[\underline{x}_{0} → \underline{x}_{1}]$ , $[\underline{x}_{0} → \underline{x}_{2}]$ and $[\underline{x}_{0} → \underline{x}_{3}]$ are not necessarily "disjoint" . An upper bound is provided by the "Union Bound":
- $${\rm Pr(Union \hspace{0.15cm}Bound)} = {\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}2}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}3}] \ge {\rm Pr(block\hspace{0.15cm}error)} \hspace{0.05cm}.$$
Another bound was given by Bhattacharyya:
- $${\rm Pr(Bhattacharyya)} = W(\beta)-1 \ge {\rm Pr(Union \hspace{0.15cm}Bound)} \ge {\rm Pr(block\:error)} \hspace{0.05cm},$$
where for the binary erasure channel, the Bhattacharyya parameter $\beta = \lambda$ and the "weight enumerator function" $W(X)$ where the pseudo-variable $X$ is to be replaced here by the Bhattacharyya parameter $\lambda$.
- The "Bhattacharyya Bound" is more or less far above the "Union Bound" depending on the channel.
- Its importance lies in the fact that the bound can be specified in the same way for different channels.
Hints: The exercise belongs to the chapter "Bounds on block error probability".
Questions
Solution
- $\underline{y} = (0, {\rm E}, 0, {\rm E}, {\rm E})$ The code words $\underline{x}_{0}$ and $\underline{x}_{1}$ differ in bit $2, \ 4$ and $5$. If only one of these three binary values is transmitted correctly, the entire codeword is thus uniquely determined. No information about the codeword is obtained for the following received vectors (see table on the information page): $\lambda^3 \ · \ (1 – \lambda)^2$,
- $\underline{y} = (0, {\rm E}, {\rm E}, {\rm E}, {\rm E})$ with probability $\lambda^4 \ · \ (1 – \lambda)$,
- $\underline{y} = ({\rm E}, {\rm E}, 0, {\rm E}, {\rm E})$ with probability $\lambda^4 \ · \ (1 – \lambda)$,
- $\underline{y} = ({\rm E}, {\rm E}, {\rm E}, {\rm E}, {\rm E})$ with probability $\lambda^5$.
The probability that, due to the specific received vector $\underline{y}$, the codeword $\underline{x}_{1}$ is just as likely as $\underline{x}_{0}$, is given by
- $$\ {\rm Pr}\ [\underline{x}_0 \hspace{0.12cm}{\rm and}\hspace{0.12cm} \underline{x}_1 \hspace{0.15cm}{\rm are \hspace{0.15cm}equally \hspace{0.15cm}probable}] = \lambda^3 \cdot (1- \lambda)^2 + 2 \cdot \lambda^4 \cdot (1- \lambda) + \lambda^5 =\lambda^3 \cdot \left [ (1- \lambda)^2 + 2 \cdot \lambda \cdot (1- \lambda) + \lambda^2 \right ] = \lambda^3 \hspace{0.05cm}.$$
In this case, one decides at random for $\underline{x}_{0}$ (would be correct) or for $\underline{x}_{1}$ (unfortunately wrong), with equal probability. From this follows:
- $${\rm Pr} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] = 1/2 \cdot \lambda^3 \hspace{0.15cm} \underline{= 0.5 \cdot 10^{-3}} \hspace{0.05cm}.$$
(2) According to subtask (1), answer 2 is correct and not answer 1. Statement 3 is also incorrect:
- ${\rm Pr}[\underline{x}_{0} → \underline{x}_{1}]$ does not state that with this probability the codeword $\underline{x}_{0}$ actually transitions to the incorrect codeword $\underline{x}_{1}$, but only that it could transition to $\underline{x}_{1}$ with this probability.
- ${\rm Pr}[\underline{x}_{0} → \underline{x}_{1}]$ also includes constellations where the decision is actually for $\underline{x}_{2}$ or $\underline{x}_{3}$.
(3) Because of $d_{\rm H}(\underline{x}_{0}, \underline{x}_{2}) = 3$ and $d_{\rm H}(\underline{x}_{0}, \underline{x}_{3}) = 4$ it follows that
- $${\rm Pr} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}] = 1/2 \cdot \lambda^3 \hspace{0.15cm} \underline{= 0.5 \cdot 10^{-3}} \hspace{0.05cm},\hspace{0.2cm} {\rm Pr} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}] = 1/2 \cdot \lambda^4 \hspace{0.15cm} \underline{= 0.05 \cdot 10^{-3}} \hspace{0.05cm}.$$
(4) The block error probability is never larger (with a certain probability rather smaller) than the so-called Union Bound:
- $${\rm Pr(Union \hspace{0.15cm}Bound)} \hspace{-0.15cm}\ = \ \hspace{-0.15cm} {\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}2}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}3}] = 2 \cdot \lambda^3/2 + \lambda^4/2 = 0.001 + 0.00005 \hspace{0.15cm} \underline{= 1.05 \cdot 10^{-3}} \hspace{0.05cm}.$$
(5) Generally speaking:
- $${\rm Pr(block\:error) ≤ {\rm Pr(Union \hspace{0.15cm}Bound)} \le Pr(Bhattacharyya)} = W(\beta) - 1.$$
- For the distance spectrum or the weight function, we obtain in the present case:
- $$W_0 = 1 \hspace{0.05cm}, \hspace{0.2cm} W_3 = 2 \hspace{0.05cm}, \hspace{0.2cm}W_4 = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} W(X) = 1+ 2 \cdot X^{3} +X^{4} \hspace{0.05cm}.$$
- For the BEC channel, $\beta = \lambda$ also applies. From this follows as a final result for $\lambda = 0.001$:
- $${\rm Pr(Bhattacharyya)} = 2 \cdot \lambda^3 + \lambda^4 \hspace{0.15cm} \underline{= 2.1 \cdot 10^{-3}} \hspace{0.05cm}.$$
Note that in the BEC model, the Bhattacharyya bound is always twice as large as the Union Bound, which is itself an upper bound on the block error probability.