Difference between revisions of "Aufgaben:Exercise 1.17Z: BPSK Channel Capacity"
| (2 intermediate revisions by one other user not shown) | |||
| Line 3: | Line 3: | ||
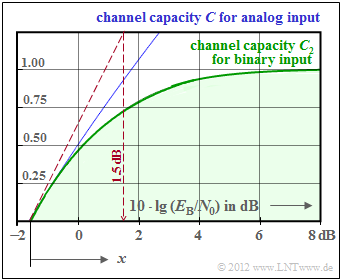
[[File:EN_KC_Z_1_17.png|right|frame|For clarification of the BPSK channel capacity]] | [[File:EN_KC_Z_1_17.png|right|frame|For clarification of the BPSK channel capacity]] | ||
| − | + | Binary signals can be transmitted error-free over the [[Channel_Coding/Channel_Models_and_Decision_Structures#AWGN_channel_at_Binary_Input|"AWGN channel"]] according to the [[Channel_Coding/Information_Theoretical_Limits_of_Channel_Coding#Channel_coding_theorem_and_channel_capacity|"channel coding theorem"]] if and only if | |
| + | |||
| + | *one uses a channel code of rate $R = k/n$, | ||
| − | |||
*the block length $n$ of this code is chosen very large ⇒ $n → ∞$, | *the block length $n$ of this code is chosen very large ⇒ $n → ∞$, | ||
| + | |||
*the rate $R$ is smaller than the channel capacity valid for binary input $C_{2}$, | *the rate $R$ is smaller than the channel capacity valid for binary input $C_{2}$, | ||
| + | |||
*where the BPSK channel capacity $C_{2}$ depends on the AWGN quotient $E_{\rm B}/N_{0}$ . | *where the BPSK channel capacity $C_{2}$ depends on the AWGN quotient $E_{\rm B}/N_{0}$ . | ||
| − | The permissible range for the code rate $R$ is highlighted in green in the graph. The limit curve $C_{2}$, valid for binary input signals $($therefore the index $2)$ and sometimes also referred to as BPSK channel capacity (stands for | + | <u>Note:</u> |
| + | #The permissible range for the code rate $R$ is highlighted in green in the graph. | ||
| + | #The limit curve $C_{2}$, valid for binary input signals $($therefore the index $2)$ and sometimes also referred to as BPSK channel capacity (stands for "Binary Phase Shift Keying"). | ||
| + | #However, this curve cannot be specified in mathematically closed form, but is the result of an integral that can only be evaluated numerically. | ||
| + | #As blue curve the channel capacity $C$ is entered, if arbitrary real input signals are allowed. | ||
| + | #For multilevel signals the rate may well assume values $R > 1$. | ||
| + | #For a Gaussian distribution the rate $R$ is the smallest possible $(E_{\rm B}/N_{0})_{\rm min}$ according to the equation | ||
| + | |||
| + | ::$$\left (E_{\rm B}/N_0 \right)_{\rm min} = \frac{2^{2R}-1}{2R}\hspace{0.05cm}.$$ | ||
| − | + | Conversely, the rate $R$ for the given AWGN quotient $E_{\rm B}/N_{0}$ is upper bounded: | |
| − | + | *The just allowable code rate $R_{\rm max}$ for a given channel $(E_{\rm B}/N_{0} = \rm const.)$ we refer to as the channel capacity $C$. | |
| − | * | ||
| − | + | *For $E_{\rm B}/N_{0} = 1 ⇒ 10 \ \lg {E_{\rm B}/N_0} = 0\ {\rm dB}$ we obtain, for example $C = 0.5$. | |
| − | + | ||
| − | + | *This means: Even with the best possible amplitude distribution of the real input signal, the code rate must not exceed $R = 0.5$. | |
| − | + | ||
| − | *For $E_{\rm B}/N_{0} = 1 ⇒ 10 | + | *For binary input, a slightly smaller value results according to $C_{2}.$ |
| − | *This means: Even with the best possible amplitude distribution of the real input signal, the code rate must not exceed $R = 0.5$ | ||
| − | *For binary input, a slightly smaller value results according to $C_{2}.$ | ||
| − | In this exercise, try to approximate the graphically given channel capacitance $C_{2}$ by an exponential function: | + | In this exercise, try to approximate the graphically given channel capacitance $C_{2}$ by an exponential function: |
| − | *For the abscissa, use the auxiliary variable (see graph) | + | *For the abscissa, use the auxiliary variable (see graph) |
:$$x = \frac {x_0 + 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 }{1\,{\rm dB}}\hspace{0.05cm}.$$ | :$$x = \frac {x_0 + 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 }{1\,{\rm dB}}\hspace{0.05cm}.$$ | ||
| − | :That is, $x$ is without unit; the pseudo unit "$\rm dB$" is omitted. | + | :That is, $x$ is without unit; the pseudo unit "$\rm dB$" is omitted. |
| − | *Consider that for a small $E_{\rm B}/N_{0}$ the approximation $C_{2} \approx C$ is valid (see graph), from which the parameter $x_{0}$ can be determined. | + | *Consider that for a small $E_{\rm B}/N_{0}$ the approximation $C_{2} \approx C$ is valid (see graph), from which the parameter $x_{0}$ can be determined. |
| − | *Set for $C_{2}\hspace{0.01cm}' = 1 - {\rm e}^{-a\hspace{0.05cm} · \hspace{0.05cm}x}$ and determine the parameter $a$ from the dashed tangent such that $C_{2}\hspace{0.01cm} ' \approx C$ holds. | + | *Set for $C_{2}\hspace{0.01cm}' = 1 - {\rm e}^{-a\hspace{0.05cm} · \hspace{0.05cm}x}$ and determine the parameter $a$ from the red dashed tangent such that $C_{2}\hspace{0.01cm} ' \approx C$ holds. |
| Line 45: | Line 53: | ||
Hints: | Hints: | ||
| − | * The exercise belongs to the chapter [[Channel_Coding/Information_Theoretical_Limits_of_Channel_Coding|"Information Theoretical Limits of Channel Coding"]]. It complements the [[Aufgaben:Exercise_1.17:_About_the_Channel_Coding_Theorem|"Exercise 1.17"]]. | + | * The exercise belongs to the chapter [[Channel_Coding/Information_Theoretical_Limits_of_Channel_Coding|"Information Theoretical Limits of Channel Coding"]]. It complements the [[Aufgaben:Exercise_1.17:_About_the_Channel_Coding_Theorem|"Exercise 1.17"]]. |
| − | * The "bit/channel use" pseudo-unit of channel capacity is omitted in these exercises. | + | |
| + | * The "bit/channel use" pseudo-unit of channel capacity is omitted in these exercises. | ||
| Line 58: | Line 67: | ||
$x_{0} \ = \ $ { 1.6 3% }$\ \rm dB$ | $x_{0} \ = \ $ { 1.6 3% }$\ \rm dB$ | ||
| − | {Approximate $C_{2}(x)$ by $C_{2}\hspace{0.01cm}'(x) = 1 -{\rm e}^{-a\hspace{0.05cm} · \hspace{0.05cm}x}$. What is the value of $a$? | + | {Approximate $C_{2}(x)$ by $C_{2}\hspace{0.01cm}'(x) = 1 -{\rm e}^{-a\hspace{0.05cm} · \hspace{0.05cm}x}$. What is the value of $a$? |
|type="{}"} | |type="{}"} | ||
$a \ = \ $ { 0.4 3% } | $a \ = \ $ { 0.4 3% } | ||
| Line 77: | Line 86: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' In the lower $E_{\rm B} /N_{0}$ range, the capacity curves | + | '''(1)''' In the lower $E_{\rm B} /N_{0}$ range, the capacity curves |
| − | *$C_{2}$ (valid for binary input, for example BPSK) and | + | *$C_{2}$ $($valid for binary input, for example BPSK$)$ and |
| − | *$C$ (valid for analog real-valued input) | + | *$C$ $($valid for analog real-valued input$)$ |
| − | converge. For a given rate $R$ $E_{\rm B}/N_{0}$ must be greater than $(2^{2R} - 1)/2R.$ | + | converge. For a given rate $R$ ⇒ $E_{\rm B}/N_{0}$ must be greater than $(2^{2R} - 1)/2R.$ |
The limit transition for $R → 0$ provides the absolute Shannon limit above which error-free transmission is no longer possible: | The limit transition for $R → 0$ provides the absolute Shannon limit above which error-free transmission is no longer possible: | ||
| Line 90: | Line 99: | ||
| − | '''(2)''' The tangent increase at the zero point can be estimated from the graph | + | '''(2)''' The tangent increase at the zero point can be estimated from the graph in the data section: |
:$$\frac{{\rm d}C_2}{{\rm d}x} (x=0) = \frac{1.6 + 1.5}{1.25} =2.48 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} a = \frac{1}{2.48} \hspace{0.15cm} \underline{\approx 0.4}\hspace{0.05cm}.$$ | :$$\frac{{\rm d}C_2}{{\rm d}x} (x=0) = \frac{1.6 + 1.5}{1.25} =2.48 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} a = \frac{1}{2.48} \hspace{0.15cm} \underline{\approx 0.4}\hspace{0.05cm}.$$ | ||
| − | Thus, the approximation for the BPSK channel capacity as a function of the abscissa value $x$ is: | + | Thus, the approximation for the BPSK channel capacity as a function of the abscissa value $x$ is: |
:$$C_2' = \hspace{0.15cm} \left\{ \begin{array}{c} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}x} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm for\hspace{0.15cm}} x > 0, \\{\rm for\hspace{0.15cm}} x < 0. \end{array}$$ | :$$C_2' = \hspace{0.15cm} \left\{ \begin{array}{c} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}x} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm for\hspace{0.15cm}} x > 0, \\{\rm for\hspace{0.15cm}} x < 0. \end{array}$$ | ||
| − | '''(3)''' From $E_{\rm B} = N_{0}$ follows $\ 10 · \lg {(E_{\rm B} = N_0)} = 0 \ {\rm dB}$ and $x = 1.6$: | + | '''(3)''' From $E_{\rm B} = N_{0}$ follows $\ 10 · \lg {(E_{\rm B} = N_0)} = 0 \ {\rm dB}$ and $x = 1.6$: |
:$$C_2\hspace{0.01cm}' = 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}1.6}\hspace{0.15cm}\underline{\approx 0.47}\hspace{0.05cm}.$$ | :$$C_2\hspace{0.01cm}' = 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}1.6}\hspace{0.15cm}\underline{\approx 0.47}\hspace{0.05cm}.$$ | ||
| Line 109: | Line 118: | ||
:$$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{6 dB:} \hspace{0.3cm} C_2\hspace{0.01cm}' \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}7.6}\hspace{0.15cm}\underline{\approx 0.95}.$$ | :$$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{6 dB:} \hspace{0.3cm} C_2\hspace{0.01cm}' \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}7.6}\hspace{0.15cm}\underline{\approx 0.95}.$$ | ||
| − | The values $C_{2}\hspace{0.01cm}'$ of the channel capacity for binary input approximated in this way are somewhat too small. | + | The values $C_{2}\hspace{0.01cm}'$ of the channel capacity for binary input approximated in this way are somewhat too small. |
| − | From the graph | + | From the graph in the information section the exact values $C_{2}$ can be estimated: |
:$$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 =\text{2 dB:} \hspace{0.3cm} C_2 \hspace{-0.15cm}\ \approx \ \hspace{-0.15cm} {0.78}\hspace{0.05cm},$$ | :$$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 =\text{2 dB:} \hspace{0.3cm} C_2 \hspace{-0.15cm}\ \approx \ \hspace{-0.15cm} {0.78}\hspace{0.05cm},$$ | ||
| Line 117: | Line 126: | ||
:$$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{6 dB:} \hspace{0.3cm} C_2 \hspace{-0.15cm}\ \approx \ \hspace{-0.15cm} {0.99}\hspace{0.05cm}.$$ | :$$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{6 dB:} \hspace{0.3cm} C_2 \hspace{-0.15cm}\ \approx \ \hspace{-0.15cm} {0.99}\hspace{0.05cm}.$$ | ||
| − | + | From about $\ 10 \cdot \lg {(E_{\rm B} / N_0)} = 8 \ {\rm dB}$ applies within character accuracy: $C_{2}\hspace{0.01cm}'= C_{2} = 1$ $($bit/channel use$)$. | |
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 18:04, 23 January 2023
Binary signals can be transmitted error-free over the "AWGN channel" according to the "channel coding theorem" if and only if
- one uses a channel code of rate $R = k/n$,
- the block length $n$ of this code is chosen very large ⇒ $n → ∞$,
- the rate $R$ is smaller than the channel capacity valid for binary input $C_{2}$,
- where the BPSK channel capacity $C_{2}$ depends on the AWGN quotient $E_{\rm B}/N_{0}$ .
Note:
- The permissible range for the code rate $R$ is highlighted in green in the graph.
- The limit curve $C_{2}$, valid for binary input signals $($therefore the index $2)$ and sometimes also referred to as BPSK channel capacity (stands for "Binary Phase Shift Keying").
- However, this curve cannot be specified in mathematically closed form, but is the result of an integral that can only be evaluated numerically.
- As blue curve the channel capacity $C$ is entered, if arbitrary real input signals are allowed.
- For multilevel signals the rate may well assume values $R > 1$.
- For a Gaussian distribution the rate $R$ is the smallest possible $(E_{\rm B}/N_{0})_{\rm min}$ according to the equation
- $$\left (E_{\rm B}/N_0 \right)_{\rm min} = \frac{2^{2R}-1}{2R}\hspace{0.05cm}.$$
Conversely, the rate $R$ for the given AWGN quotient $E_{\rm B}/N_{0}$ is upper bounded:
- The just allowable code rate $R_{\rm max}$ for a given channel $(E_{\rm B}/N_{0} = \rm const.)$ we refer to as the channel capacity $C$.
- For $E_{\rm B}/N_{0} = 1 ⇒ 10 \ \lg {E_{\rm B}/N_0} = 0\ {\rm dB}$ we obtain, for example $C = 0.5$.
- This means: Even with the best possible amplitude distribution of the real input signal, the code rate must not exceed $R = 0.5$.
- For binary input, a slightly smaller value results according to $C_{2}.$
In this exercise, try to approximate the graphically given channel capacitance $C_{2}$ by an exponential function:
- For the abscissa, use the auxiliary variable (see graph)
- $$x = \frac {x_0 + 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 }{1\,{\rm dB}}\hspace{0.05cm}.$$
- That is, $x$ is without unit; the pseudo unit "$\rm dB$" is omitted.
- Consider that for a small $E_{\rm B}/N_{0}$ the approximation $C_{2} \approx C$ is valid (see graph), from which the parameter $x_{0}$ can be determined.
- Set for $C_{2}\hspace{0.01cm}' = 1 - {\rm e}^{-a\hspace{0.05cm} · \hspace{0.05cm}x}$ and determine the parameter $a$ from the red dashed tangent such that $C_{2}\hspace{0.01cm} ' \approx C$ holds.
Hints:
- The exercise belongs to the chapter "Information Theoretical Limits of Channel Coding". It complements the "Exercise 1.17".
- The "bit/channel use" pseudo-unit of channel capacity is omitted in these exercises.
Questions
Solution
(1) In the lower $E_{\rm B} /N_{0}$ range, the capacity curves
- $C_{2}$ $($valid for binary input, for example BPSK$)$ and
- $C$ $($valid for analog real-valued input$)$
converge. For a given rate $R$ ⇒ $E_{\rm B}/N_{0}$ must be greater than $(2^{2R} - 1)/2R.$
The limit transition for $R → 0$ provides the absolute Shannon limit above which error-free transmission is no longer possible:
- $${\rm Min}\hspace{0.1cm}\left [E_{\rm B}/N_0 \right] = \lim_{R \rightarrow 0}\hspace{0.1cm} \frac{2^{2R}-1}{2R} = {\rm ln}\hspace{0.1cm}2 \approx 0.693\hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm} {\rm Min}\hspace{0.1cm}\left [E_{\rm B}/N_0 \right] \approx -1.6 \,{\rm dB} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x_0 \hspace{0.15cm} \underline{= 1.6 \,{\rm dB}}\hspace{0.05cm}.$$
(2) The tangent increase at the zero point can be estimated from the graph in the data section:
- $$\frac{{\rm d}C_2}{{\rm d}x} (x=0) = \frac{1.6 + 1.5}{1.25} =2.48 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} a = \frac{1}{2.48} \hspace{0.15cm} \underline{\approx 0.4}\hspace{0.05cm}.$$
Thus, the approximation for the BPSK channel capacity as a function of the abscissa value $x$ is:
- $$C_2' = \hspace{0.15cm} \left\{ \begin{array}{c} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}x} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm for\hspace{0.15cm}} x > 0, \\{\rm for\hspace{0.15cm}} x < 0. \end{array}$$
(3) From $E_{\rm B} = N_{0}$ follows $\ 10 · \lg {(E_{\rm B} = N_0)} = 0 \ {\rm dB}$ and $x = 1.6$:
- $$C_2\hspace{0.01cm}' = 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}1.6}\hspace{0.15cm}\underline{\approx 0.47}\hspace{0.05cm}.$$
(4) The corresponding numerical values are:
- $$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{2 dB:} \hspace{0.3cm} C_2\hspace{0.01cm}' \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}3.6}\hspace{0.15cm}\underline{\approx 0.76}$$
- $$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{4 dB:} \hspace{0.3cm} C_2\hspace{0.01cm}' \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}5.6}\hspace{0.15cm}\underline{\approx 0.89}$$
- $$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{6 dB:} \hspace{0.3cm} C_2\hspace{0.01cm}' \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}7.6}\hspace{0.15cm}\underline{\approx 0.95}.$$
The values $C_{2}\hspace{0.01cm}'$ of the channel capacity for binary input approximated in this way are somewhat too small.
From the graph in the information section the exact values $C_{2}$ can be estimated:
- $$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 =\text{2 dB:} \hspace{0.3cm} C_2 \hspace{-0.15cm}\ \approx \ \hspace{-0.15cm} {0.78}\hspace{0.05cm},$$
- $$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{4 dB:} \hspace{0.3cm} C_2 \hspace{-0.15cm}\ \approx \ \hspace{-0.15cm} {0.94}\hspace{0.05cm},$$
- $$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{6 dB:} \hspace{0.3cm} C_2 \hspace{-0.15cm}\ \approx \ \hspace{-0.15cm} {0.99}\hspace{0.05cm}.$$
From about $\ 10 \cdot \lg {(E_{\rm B} / N_0)} = 8 \ {\rm dB}$ applies within character accuracy: $C_{2}\hspace{0.01cm}'= C_{2} = 1$ $($bit/channel use$)$.