Difference between revisions of "Aufgaben:Exercise 1.1Z: Low-Pass Filter of 1st and 2nd Order"
m (Text replacement - "analyse" to "analyze") |
|||
| (44 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Linear_and_Time_Invariant_Systems/System_Description_in_Frequency_Domain}} |
| − | + | [[File:P_ID785__LZI_Z_1_1.png|Damping– & phase function|right|frame]] | |
| − | [[File:P_ID785__LZI_Z_1_1.png| | + | The simplest form of a low-pass filter – for example, realisable as an RC low-pass filter according to [[Aufgaben:Exercise_1.1:_Simple_Filter_Functions|Exercise 1.1]] – has the following frequency response: |
| − | + | :$$H_{\rm 1}(f) = \frac{1}{1+{\rm j}\cdot f/f_0}.$$ | |
| − | $$H_{\rm 1}(f) = \frac{1}{1+{\rm j}\cdot f/f_0}.$$ | + | This is then referred to as a low-pass filter of first order. The diagram shows the following for this filter |
| − | + | * above the "damping curve" $a_1(f)$, | |
| − | * | + | * below the "phase response" $b_1(f)$. |
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Correspondingly, for a low-pass filter of $n$–th order the following defining equation applies: | ||
| + | :$$H_n(f) = H_{\rm 1}(f)^n.$$ | ||
| − | '' | + | |
| − | * | + | In this task, |
| − | * | + | *based on the functions $a_1(f)$ and $b_1(f)$ of the low-pass filter of first order |
| − | + | *the damping curve and phase response of a low-pass filter of higher order is to be analyzed. | |
| − | $$a_{\rm Np} = \ln (x) = \ln (10) \cdot \lg (x) = \frac{\ln | + | |
| + | |||
| + | In general, the following holds: | ||
| + | :$$H(f) = {\rm e}^{-a(f) - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}b(f)}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hint:'' | ||
| + | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/System_Description_in_Frequency_Domain | System Description in Frequency Domain]]. | ||
| + | |||
| + | *There is the following relationship between the Np- and dB-values of an amplitude value $|H| = 1/x$ : | ||
| + | :$$a_{\rm Np} = \ln (x) = \ln (10) \cdot \lg (x) = \frac{\ln | ||
(10)}{20} \cdot a_{\rm dB} \approx 0.11513 \cdot a_{\rm dB}.$$ | (10)}{20} \cdot a_{\rm dB} \approx 0.11513 \cdot a_{\rm dB}.$$ | ||
| − | * | + | *Further consider that for two complex quantities $z_1$ and $z_2$ the following equations hold: |
| − | $$|z_1 \cdot z_2| = |z_1| \cdot |z_2|, \hspace{0.5 cm}{\rm arc}\hspace{0.05 cm}(z_1 \cdot z_2) = {\rm arc}\hspace{0.05 cm}(z_1) + {\rm arc}\hspace{0.05 cm}(z_2).$$ | + | :$$|z_1 \cdot z_2| = |z_1| \cdot |z_2|, \hspace{0.5 cm}{\rm arc}\hspace{0.05 cm}(z_1 \cdot z_2) = {\rm arc}\hspace{0.05 cm}(z_1) + {\rm arc}\hspace{0.05 cm}(z_2).$$ |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Compute the damping curve $a_1(f)$ of a low-pass filter of first order in $\rm dB$. <br>What $\rm dB$ values are obtained for $f = f_0$ and $f = 2f_0$? |
|type="{}"} | |type="{}"} | ||
| − | $a_1(f = f_0)$ | + | $a_1(f = f_0)\ = \ $ { 3.01 5% } $\text{dB}$ |
| − | $a_1(f = 2f_0)$ | + | $a_1(f = 2f_0)\ = \ $ { 6.99 5% } $\text{dB}$ |
| − | { | + | {Compute the phase response $b_1(f)$. <br>What values in radian (rad) are obtained for $f = f_0$ and $f = 2f_0$? |
|type="{}"} | |type="{}"} | ||
| − | $b_1(f = f_0)$ | + | $b_1(f = f_0)\ = \ $ { 0.786 5% } $\text{rad}$ |
| − | $b_1(f = 2f_0)$ | + | $b_1(f = 2f_0)\ = \ $ { 1.108 5% } $\text{rad}$ |
| − | { | + | {What is the damping curve $a_n(f)$ of a low-pass filter of $n$–th order? <br>What $\rm dB$ values are obtained for $n = 2$ for $f = f_0$ or $f = \: –2f_0$? |
|type="{}"} | |type="{}"} | ||
| − | $a_2(f = f_0)$ | + | $a_2(f = f_0)\ = \ $ { 6.02 5% } $\text{dB}$ |
| − | $a_2(f = -2f_0)$ | + | $a_2(f = -2f_0)\ = \ $ { 13.98 5% } $\text{dB}$ |
| − | { | + | {Compute the phase function $b_2(f)$ of a low-pass filter of second order. <br>What values (in radian) are obtained for $f = f_0$ and $f = \: –2f_0$? |
|type="{}"} | |type="{}"} | ||
| − | $b_2(f = f_0)$ | + | $b_2(f = f_0)\ = \ $ { 1.571 5% } $\text{rad}$ |
| − | $b_2(f = -2f_0)$ | + | $b_2(f = -2f_0)\ = \ $ { -2.23--2.20 } $\text{rad}$ |
| Line 57: | Line 68: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The amplitude response of the low-pass filter of first order is: |
| − | $$|H_{\rm 1}(f)| = \frac{1}{\sqrt{1+ (f/f_0)^2}}.$$ | + | :$$|H_{\rm 1}(f)| = \frac{1}{\sqrt{1+ (f/f_0)^2}}.$$ |
| − | + | *This gives the damping curve in Neper (Np): | |
| − | $$ | + | :$$a_1(f) = \ln \frac{1}{|H_1(f)|} = {1}/{2} \cdot \ln \left[1 + ({f}/{f_0})^2 \right] \Rightarrow a_1(f = f_0) = 0.3466 \hspace{0.1 cm}{\rm Np},\hspace{0.5 cm}a_1(f = 2 f_0) = 0.8047 \hspace{0.1 cm}{\rm Np}.$$ |
| − | 0. | + | The corresponding dB values are obtained by multiplying by $1/0.11513 = 8.68589$ and result in |
| − | + | *$ \underline{3.01 \: {\rm dB} ≈ 3 \: {\rm dB}}$ für $ f = f_0$, | |
| + | *$ \underline{6.99 \: {\rm dB}}$ für $ f = 2f_0$. | ||
| + | |||
| + | |||
| + | Thus, for the low-pass filter of first order the 3dB cut-off frequency is $f_{\rm G} = f_0$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' The frequency response $H_1(f)$ can also be represented separately by thr real and the imaginary part: | ||
| + | :$$H_{\rm 1}(f) = \frac{1}{ {1+ (f/f_0)^2} } - {\rm j} \cdot \frac{f/f_0}{ {1+ (f/f_0)^2} }.$$ | ||
| + | *Hence, the following holds for the phase response: | ||
| + | :$$b_1(f) = - \arctan \hspace{0.1cm} ( {\rm Im} /{\rm Re} ) = \arctan \hspace{0.1cm} ({f}/{f_0}).$$ | ||
| + | *The value $\arctan(1) = π/4 \rm \underline{\: = 0.786 \: rad}$ is obtained for $f = f_0$ and $\arctan(2) \rm \underline{\: = 1.108 \: rad}$ for $f = 2f_0$ . | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' For the amplitude response of a low-pass filter of $n$–th order the following is valid: | ||
| + | :$$|H_n(f)| = |H_{\rm 1}(f)|^n.$$ | ||
| + | Regarding the (logarithmic) damping function the $n$–fold multiplication becomes the $n$–fold sum: | ||
| + | :$$a_n(f) = n \cdot a_1(f)= {n}/{2} \cdot \ln \left[ 1 + ({f}/{f_0})^2 \right].$$ | ||
| + | For the low-pass filter of second order this results in the special case: | ||
| + | :$$a_2(f) = \ln \left[ 1 + ({f}/{f_0})^2 \right]= 2 \cdot a_1(f).$$ | ||
| + | The dB values are now: | ||
| + | *$ \underline{6.02 \: {\rm dB} ≈ 6 \: {\rm dB}}$ für $f = ±f_0$, | ||
| + | *$\rm \underline{13.98 \: {\rm dB} ≈ 14 \: {\rm dB}}$ für $f = ±2f_0$. | ||
| − | + | It is thus obvious that for $n > 1$ the parameter $f_0$ no longer indicates the 3dB cut off frequency $f_{\rm G}$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | For $n = 2$ ⇒ "low-pass filter of second order" the following relationship applies instead: | ||
| + | :$${f_{\rm G} } = {f_0}/\sqrt{2}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(4)''' Also, with respect to the phase function the following holds: | |
| + | :$$b_n(f) = n \cdot b_1(f), \hspace{0.3 cm} b_2(f) = 2 \cdot b_1(f).$$ | ||
| + | Thus, for the low-pass filter of second order all phase values between $±π$ are possible. In particular the following holds: | ||
| + | *$b_2(f = f_0) = π/2 \rm \underline{\: = 1.571 \: rad}$, | ||
| + | * $b_2(f = 2f_0) = \rm 2.216 \: rad$. | ||
| − | + | Since "phase" is an odd function the following applies to it: $b_2(f = \: –2f_0) = \rm \underline{–2.216 \: rad}$. | |
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Linear and Time-Invariant Systems: Exercises|^1.1 System Description in Frequency Domain^]] |
Latest revision as of 13:47, 22 September 2021
The simplest form of a low-pass filter – for example, realisable as an RC low-pass filter according to Exercise 1.1 – has the following frequency response:
- $$H_{\rm 1}(f) = \frac{1}{1+{\rm j}\cdot f/f_0}.$$
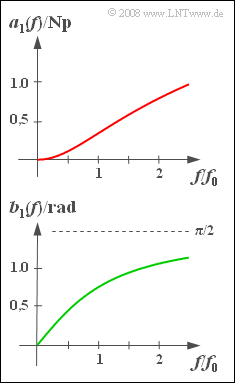
This is then referred to as a low-pass filter of first order. The diagram shows the following for this filter
- above the "damping curve" $a_1(f)$,
- below the "phase response" $b_1(f)$.
Correspondingly, for a low-pass filter of $n$–th order the following defining equation applies:
- $$H_n(f) = H_{\rm 1}(f)^n.$$
In this task,
- based on the functions $a_1(f)$ and $b_1(f)$ of the low-pass filter of first order
- the damping curve and phase response of a low-pass filter of higher order is to be analyzed.
In general, the following holds:
- $$H(f) = {\rm e}^{-a(f) - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}b(f)}.$$
Hint:
- The exercise belongs to the chapter System Description in Frequency Domain.
- There is the following relationship between the Np- and dB-values of an amplitude value $|H| = 1/x$ :
- $$a_{\rm Np} = \ln (x) = \ln (10) \cdot \lg (x) = \frac{\ln (10)}{20} \cdot a_{\rm dB} \approx 0.11513 \cdot a_{\rm dB}.$$
- Further consider that for two complex quantities $z_1$ and $z_2$ the following equations hold:
- $$|z_1 \cdot z_2| = |z_1| \cdot |z_2|, \hspace{0.5 cm}{\rm arc}\hspace{0.05 cm}(z_1 \cdot z_2) = {\rm arc}\hspace{0.05 cm}(z_1) + {\rm arc}\hspace{0.05 cm}(z_2).$$
Questions
Solution
- $$|H_{\rm 1}(f)| = \frac{1}{\sqrt{1+ (f/f_0)^2}}.$$
- This gives the damping curve in Neper (Np):
- $$a_1(f) = \ln \frac{1}{|H_1(f)|} = {1}/{2} \cdot \ln \left[1 + ({f}/{f_0})^2 \right] \Rightarrow a_1(f = f_0) = 0.3466 \hspace{0.1 cm}{\rm Np},\hspace{0.5 cm}a_1(f = 2 f_0) = 0.8047 \hspace{0.1 cm}{\rm Np}.$$
The corresponding dB values are obtained by multiplying by $1/0.11513 = 8.68589$ and result in
- $ \underline{3.01 \: {\rm dB} ≈ 3 \: {\rm dB}}$ für $ f = f_0$,
- $ \underline{6.99 \: {\rm dB}}$ für $ f = 2f_0$.
Thus, for the low-pass filter of first order the 3dB cut-off frequency is $f_{\rm G} = f_0$.
(2) The frequency response $H_1(f)$ can also be represented separately by thr real and the imaginary part:
- $$H_{\rm 1}(f) = \frac{1}{ {1+ (f/f_0)^2} } - {\rm j} \cdot \frac{f/f_0}{ {1+ (f/f_0)^2} }.$$
- Hence, the following holds for the phase response:
- $$b_1(f) = - \arctan \hspace{0.1cm} ( {\rm Im} /{\rm Re} ) = \arctan \hspace{0.1cm} ({f}/{f_0}).$$
- The value $\arctan(1) = π/4 \rm \underline{\: = 0.786 \: rad}$ is obtained for $f = f_0$ and $\arctan(2) \rm \underline{\: = 1.108 \: rad}$ for $f = 2f_0$ .
(3) For the amplitude response of a low-pass filter of $n$–th order the following is valid:
- $$|H_n(f)| = |H_{\rm 1}(f)|^n.$$
Regarding the (logarithmic) damping function the $n$–fold multiplication becomes the $n$–fold sum:
- $$a_n(f) = n \cdot a_1(f)= {n}/{2} \cdot \ln \left[ 1 + ({f}/{f_0})^2 \right].$$
For the low-pass filter of second order this results in the special case:
- $$a_2(f) = \ln \left[ 1 + ({f}/{f_0})^2 \right]= 2 \cdot a_1(f).$$
The dB values are now:
- $ \underline{6.02 \: {\rm dB} ≈ 6 \: {\rm dB}}$ für $f = ±f_0$,
- $\rm \underline{13.98 \: {\rm dB} ≈ 14 \: {\rm dB}}$ für $f = ±2f_0$.
It is thus obvious that for $n > 1$ the parameter $f_0$ no longer indicates the 3dB cut off frequency $f_{\rm G}$.
For $n = 2$ ⇒ "low-pass filter of second order" the following relationship applies instead:
- $${f_{\rm G} } = {f_0}/\sqrt{2}.$$
(4) Also, with respect to the phase function the following holds:
- $$b_n(f) = n \cdot b_1(f), \hspace{0.3 cm} b_2(f) = 2 \cdot b_1(f).$$
Thus, for the low-pass filter of second order all phase values between $±π$ are possible. In particular the following holds:
- $b_2(f = f_0) = π/2 \rm \underline{\: = 1.571 \: rad}$,
- $b_2(f = 2f_0) = \rm 2.216 \: rad$.
Since "phase" is an odd function the following applies to it: $b_2(f = \: –2f_0) = \rm \underline{–2.216 \: rad}$.