Difference between revisions of "Aufgaben:Exercise 1.3: Channel Models BSC - BEC - BSEC - AWGN"
| (24 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel Coding/Channel Models and Decision Structures |
}} | }} | ||
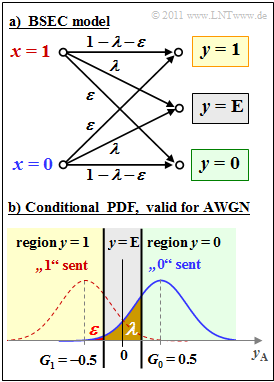
| − | [[File: | + | [[File:EN_KC_A_1_3.png|right|frame|Channel models "BSEC" and "AWGN"]] |
| − | + | The theory section for this chapter covers the following digital channel models: | |
| − | *[[ | + | *[[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Symmetric_Channel_.E2.80.93_BSC|Binary Symmetric Channel]] $\rm (BSC)$, |
| − | *[[ | + | *[[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Erasure_Channel_.E2.80.93_BEC|Binary Erasure Channel]] $\rm (BEC)$, |
| − | *[[ | + | *[[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Symmetric_Error_.26_Erasure_Channel_.E2.80.93_BSEC|Binary Symmetric Error & Erasure Channel]] $\rm (BSEC)$. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The upper graph shows the BSEC model. Two other channel models can be derived from it: | |
| + | *With $λ = 0$ the BSC model is obtained. | ||
| + | *With $\varepsilon = 0$ the BEC model results. | ||
| − | |||
| − | + | The lower graph shows the relationship between the discrete BSEC model and the analog AWGN model. To avoid confusion, we denote the (analog) output signal of the AWGN model by $y_{\rm A}$, where with the noise term $n$ holds: | |
| − | + | :$$y_{\rm A} = \tilde{x}+ n.$$ | |
| + | |||
| + | The tilde indicates the bipolar description of the digital signal. It holds: | ||
| + | *$\tilde{x} = +1$, if $x = 0$, | ||
| + | *$\tilde{x} = -1$, if $x = 1$. | ||
| + | |||
| + | |||
| + | One can see the ternary output variable $y \in \{0, 1, \rm E\}$, which is obtained from the AWGN model by dividing it into three areas. For this, the decision thresholds $G_0$ and $G_1$ are needed. | ||
| + | |||
| + | The event $y = \rm E$ ("Erasure") states that the decision is so uncertain that as result neither $y = 0$ nor $y = 1$ seems justified. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | *This exercise belongs to the chapter [[Channel_Coding/Channel_Models_and_Decision_Structures|"Channel Models and Decision Structures"]]. | ||
| + | |||
| + | *The standard deviation (root mean square) of the AWGN noise $n$ is assumed to $\sigma = 0.4$ for the entire exercise. | ||
| + | |||
| + | *The probability that the random variable $n$ is greater than $A$ or less than $-A$ is given by the complementary Gaussian error integral ${\rm Q}(x)$ as follows: | ||
:$${\rm Pr}(n > A) = {\rm Pr}(n < -A) = {\rm Q}(A/\sigma)\hspace{0.05cm}.$$ | :$${\rm Pr}(n > A) = {\rm Pr}(n < -A) = {\rm Q}(A/\sigma)\hspace{0.05cm}.$$ | ||
| − | + | *Please note further: Starting from the AWGN model, the falsification probability $\varepsilon = 0$ is actually impossible. | |
| − | :$$ {\rm Q}(0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 50\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(0.5) \ = \ 30.85\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(1) \ = \ 15.87\% \hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(1.5) \ = \ 6.68\%\hspace{0.05cm},$$ | + | |
| − | :$${\rm Q}(2) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2.28\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(2.5) \ = \ 0.62\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(3) \ = \ 0.14\% \hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(3.5) \ = \ 0.02\% \hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(4) \approx 0 \hspace{0.05cm}.$$ | + | *For this task, we make do by specifying all probabilities as percentages with two decimal places. Thus $\varepsilon \le 0.5 \cdot 10^{-4}=0.005\%$ can be approximated by $\varepsilon \approx 0$. |
| − | + | ||
| + | |||
| + | |||
| + | The following are some numerical values of the Q-function: | ||
| + | :$$ {\rm Q}(0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 50.0\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(0.5) \ = \ 30.85\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(1) \ = \ 15.87\% \hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(1.5) \ = \ 6.68\%\hspace{0.05cm},$$ | ||
| + | :$${\rm Q}(2) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2.28\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(2.5) \ = \hspace{0.3cm} 0.62\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(3) \ = \hspace{0.3cm} 0.14\% \hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(3.5) \ = \hspace{0.3cm} 0.02\% \hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(4) \approx 0 \hspace{0.05cm}.$$ | ||
| + | |||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which decision threshold(s) gives rise to the BSC model? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + One decision threshold at $G = 0$. |
| − | - | + | - Two symmetric decision thresholds at $±G$. |
| − | - | + | - One decision threshold at $G_{1} = 0$ and a second at $G_{2} = 0.5$. |
| − | { | + | {What is the BSC falsification probability $\varepsilon$ with $\sigma = 0.4$? |
|type="{}"} | |type="{}"} | ||
| − | $\varepsilon \ = \ $ { 0.62 3% } | + | $\varepsilon \ = \ $ { 0.62 3% } $\ \%$ |
| − | { | + | {Which decision threshold(s) gives rise to the BSEC model? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - One decision threshold at $G = 0$. |
| − | + | + | + Two symmetric decision thresholds at $±G$. |
| − | - | + | - One decision threshold at $G_{1} = 0$ and a second at $G_{2} = 0.5$. |
| − | { | + | {What BSEC parameters result with thresholds at $±0.2$? |
|type="{}"} | |type="{}"} | ||
| − | $\varepsilon \ = \ $ { 0.14 3% } | + | $\varepsilon \ = \ $ { 0.14 3% } $ \ \%$ |
| − | $\lambda \ = \ $ { 2.14 3% } | + | $\lambda \ = \ $ { 2.14 3% } $ \ \%$ |
| − | |||
| − | |||
| − | |||
| − | { | + | {By which decision threshold(s) does the BEC model arise? Please refer to the last note in the information section. |
|type="[]"} | |type="[]"} | ||
| − | - | + | - One decision threshold at $G = 0$. |
| − | + | + | + Two symmetric decision thresholds at $±G$. |
| − | - | + | - One decision threshold at $G_{1} = 0$ and a second at $G_{2} = 0.5$. |
| − | { | + | {Calculate the BEC parameter $\lambda$ for decision thresholds at $G = ±0.6$. |
|type="{}"} | |type="{}"} | ||
| − | $\lambda \ = \ $ { 15.87 3% } | + | $\lambda \ = \ $ { 15.87 3% } $ \ \%$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct is <u>answer 1</u>: |
| + | *The BSC model is based on a single decision threshold. Because of the "symmetric" property, this is at $G = 0$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' The probability that a Gaussian random variable with standard deviation $\sigma$ is greater than $+1$ or less than $-1$ is given by $\varepsilon = {\rm Q} (1/ \sigma)$. | ||
| + | *With $\sigma= 0.4$ it follows: $\varepsilon = {\rm Q}(2.5) \ \underline { = 0.62\, \%}.$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' The correct answer here is <u>answer 2</u>: | ||
| + | *In the BSEC model, there are three decision regions, one each for symbols $0$ and $1$, and another for "Erasure" $\rm (E$: no decision possible$)$. | ||
| + | *To do this, we need two thresholds that must be symmetric about $0$. | ||
| + | *If this were not so, different results would result for the symbols $0$ and $1$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Let $y_{\rm A} = \tilde{x}+ n$ hold. A wrong decision results in this case for the noise term | ||
| + | *$n > +1.2$ if $\tilde{x} = -1$ ⇒ $x = 1$, | ||
| + | *$n < -1.2$, if $\tilde{x} = +1$ ⇒ $x = 0$. | ||
| − | |||
| + | In both cases, we obtain for the falsification probability: | ||
| + | :$$ε = {\rm Q}(1.2/0.4) = {\rm Q}(3) \hspace{0.15cm} \underline{=0.14 \%}.$$ | ||
| + | *An "Erasure" (no decision) results for $-0.2 < y_{\rm A} < +0.2$. | ||
| + | *Based on $\tilde{x} = -1$, it thus holds: | ||
| + | :$$\lambda \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(0.8 < n < 1.2) = {\rm Pr}(n > 0.8) - {\rm Pr}(n > 1.2) = {\rm Q}(2) - {\rm Q}(3) \approx 2.28\,\% - 0.14\,\% \hspace{0.15cm} \underline {\approx 2.14\,\%} \hspace{0.05cm}.$$ | ||
| − | |||
| + | '''(5)''' Here, <u>answer 2</u> is correct: | ||
| + | *Also in the BEC model there are two thresholds symmetric about $0$. | ||
| + | *The difference with the BSEC model is that the falsification probability $\varepsilon = 0$ (more precisely, $\varepsilon < 0.5 \cdot 10^{-4}$) arises either because | ||
| + | :*the safety range $(±G)$ is chosen larger than in the BSEC model, or | ||
| + | :*the AWGN noise has a smaller standard deviation $σ$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''( | + | '''(6)''' In the BEC model, the falsification probability is negligible: |
| + | :$$\varepsilon = {\rm Q}(1.6/0.4) = {\rm Q}(4)\approx 0.32 \cdot 10^{-4} \approx 0 \hspace{0.05cm}.$$ | ||
| + | *This means: One can actually assume the BEC model here. | ||
| + | *For the "Erasure" probability, the following holds: | ||
| + | :$${\it \lambda} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(0.4 < n < 1.6) = {\rm Pr}(n > 0.4) - {\rm Pr}(n > 1.6) ={\rm Q}(1) - {\rm Q}(4) \approx {\rm Q}(1) \hspace{0.15cm} \underline {= 15.87\,\%} \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Channel Coding: Exercises|^1.2 Channel and Decision Device^]] |
| − | ^]] | ||
Latest revision as of 17:57, 23 January 2023
The theory section for this chapter covers the following digital channel models:
- Binary Symmetric Channel $\rm (BSC)$,
- Binary Erasure Channel $\rm (BEC)$,
- Binary Symmetric Error & Erasure Channel $\rm (BSEC)$.
The upper graph shows the BSEC model. Two other channel models can be derived from it:
- With $λ = 0$ the BSC model is obtained.
- With $\varepsilon = 0$ the BEC model results.
The lower graph shows the relationship between the discrete BSEC model and the analog AWGN model. To avoid confusion, we denote the (analog) output signal of the AWGN model by $y_{\rm A}$, where with the noise term $n$ holds:
- $$y_{\rm A} = \tilde{x}+ n.$$
The tilde indicates the bipolar description of the digital signal. It holds:
- $\tilde{x} = +1$, if $x = 0$,
- $\tilde{x} = -1$, if $x = 1$.
One can see the ternary output variable $y \in \{0, 1, \rm E\}$, which is obtained from the AWGN model by dividing it into three areas. For this, the decision thresholds $G_0$ and $G_1$ are needed.
The event $y = \rm E$ ("Erasure") states that the decision is so uncertain that as result neither $y = 0$ nor $y = 1$ seems justified.
Hints:
- This exercise belongs to the chapter "Channel Models and Decision Structures".
- The standard deviation (root mean square) of the AWGN noise $n$ is assumed to $\sigma = 0.4$ for the entire exercise.
- The probability that the random variable $n$ is greater than $A$ or less than $-A$ is given by the complementary Gaussian error integral ${\rm Q}(x)$ as follows:
- $${\rm Pr}(n > A) = {\rm Pr}(n < -A) = {\rm Q}(A/\sigma)\hspace{0.05cm}.$$
- Please note further: Starting from the AWGN model, the falsification probability $\varepsilon = 0$ is actually impossible.
- For this task, we make do by specifying all probabilities as percentages with two decimal places. Thus $\varepsilon \le 0.5 \cdot 10^{-4}=0.005\%$ can be approximated by $\varepsilon \approx 0$.
The following are some numerical values of the Q-function:
- $$ {\rm Q}(0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 50.0\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(0.5) \ = \ 30.85\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(1) \ = \ 15.87\% \hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(1.5) \ = \ 6.68\%\hspace{0.05cm},$$
- $${\rm Q}(2) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2.28\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(2.5) \ = \hspace{0.3cm} 0.62\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(3) \ = \hspace{0.3cm} 0.14\% \hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(3.5) \ = \hspace{0.3cm} 0.02\% \hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(4) \approx 0 \hspace{0.05cm}.$$
Questions
Solution
- The BSC model is based on a single decision threshold. Because of the "symmetric" property, this is at $G = 0$.
(2) The probability that a Gaussian random variable with standard deviation $\sigma$ is greater than $+1$ or less than $-1$ is given by $\varepsilon = {\rm Q} (1/ \sigma)$.
- With $\sigma= 0.4$ it follows: $\varepsilon = {\rm Q}(2.5) \ \underline { = 0.62\, \%}.$
(3) The correct answer here is answer 2:
- In the BSEC model, there are three decision regions, one each for symbols $0$ and $1$, and another for "Erasure" $\rm (E$: no decision possible$)$.
- To do this, we need two thresholds that must be symmetric about $0$.
- If this were not so, different results would result for the symbols $0$ and $1$.
(4) Let $y_{\rm A} = \tilde{x}+ n$ hold. A wrong decision results in this case for the noise term
- $n > +1.2$ if $\tilde{x} = -1$ ⇒ $x = 1$,
- $n < -1.2$, if $\tilde{x} = +1$ ⇒ $x = 0$.
In both cases, we obtain for the falsification probability:
- $$ε = {\rm Q}(1.2/0.4) = {\rm Q}(3) \hspace{0.15cm} \underline{=0.14 \%}.$$
- An "Erasure" (no decision) results for $-0.2 < y_{\rm A} < +0.2$.
- Based on $\tilde{x} = -1$, it thus holds:
- $$\lambda \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(0.8 < n < 1.2) = {\rm Pr}(n > 0.8) - {\rm Pr}(n > 1.2) = {\rm Q}(2) - {\rm Q}(3) \approx 2.28\,\% - 0.14\,\% \hspace{0.15cm} \underline {\approx 2.14\,\%} \hspace{0.05cm}.$$
(5) Here, answer 2 is correct:
- Also in the BEC model there are two thresholds symmetric about $0$.
- The difference with the BSEC model is that the falsification probability $\varepsilon = 0$ (more precisely, $\varepsilon < 0.5 \cdot 10^{-4}$) arises either because
- the safety range $(±G)$ is chosen larger than in the BSEC model, or
- the AWGN noise has a smaller standard deviation $σ$.
(6) In the BEC model, the falsification probability is negligible:
- $$\varepsilon = {\rm Q}(1.6/0.4) = {\rm Q}(4)\approx 0.32 \cdot 10^{-4} \approx 0 \hspace{0.05cm}.$$
- This means: One can actually assume the BEC model here.
- For the "Erasure" probability, the following holds:
- $${\it \lambda} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(0.4 < n < 1.6) = {\rm Pr}(n > 0.4) - {\rm Pr}(n > 1.6) ={\rm Q}(1) - {\rm Q}(4) \approx {\rm Q}(1) \hspace{0.15cm} \underline {= 15.87\,\%} \hspace{0.05cm}.$$