Difference between revisions of "Aufgaben:Exercise 1.6: Autocorrelation Function and PDS with Rice Fading"
m (Javier verschob die Seite Exercises:Exercise 1.6: Autocorrelation Function and PSD with Rice Fading nach Exercise 1.6: Autocorrelation Function and PSD with Rice Fading) |
|||
| Line 2: | Line 2: | ||
{{quiz-Header|Buchseite=Mobile Kommunikation/Nichtfrequenzselektives Fading mit Direktkomponente}} | {{quiz-Header|Buchseite=Mobile Kommunikation/Nichtfrequenzselektives Fading mit Direktkomponente}} | ||
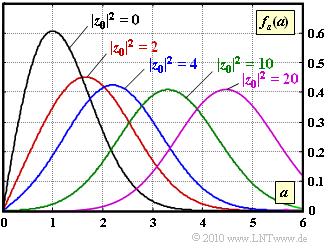
| − | [[File:P_ID2132__Mob_A_1_6.png|right|frame|Rice | + | [[File:P_ID2132__Mob_A_1_6.png|right|frame|Rice PDF for different values of $z_0^2$]] |
| − | + | One speaks of <i>Rice fading</i> if the complex factor describing the mobile radio channel contains $z(t)$ besides the purely stochastic component $x(t) +{\rm j} \cdot y(t)$ a deterministic part of the form $x_0 + {\rm j} \cdot y_0$ . | |
| − | + | The equations of Rice fading can be summarized briefly as follows: | |
:$$r(t) = z(t) \cdot s(t) ,$$ | :$$r(t) = z(t) \cdot s(t) ,$$ | ||
:$$z(t) = x(t) + {\rm j} \cdot y(t) ,$$ | :$$z(t) = x(t) + {\rm j} \cdot y(t) ,$$ | ||
| Line 11: | Line 11: | ||
:$$y(t) = v(t) + y_0 .$$ | :$$y(t) = v(t) + y_0 .$$ | ||
| − | + | The following applies: | |
| − | * | + | * The direct path is defined by the complex constant $z_0 = x_0 + {\rm j} \cdot y_0$ . The magnitude of this time-invariant component is |
:$$|z_0| = \sqrt{x_0^2 + y_0^2}\hspace{0.05cm}.$$ | :$$|z_0| = \sqrt{x_0^2 + y_0^2}\hspace{0.05cm}.$$ | ||
| − | * $u(t)$ | + | * $u(t)$ and $v(t)$ are zero-mean Gaussian random processes, both with variance $\sigma^2$ and uncorrelated with each other. They model scattering, refraction; and diffraction effects on a variety of indirect paths. |
| − | * | + | * The magnitude $a(t) = |z(t)|$ has a Rice PDF, which gives this channel model its name. For $a ≥ 0$, the PDF is |
:$$f_a(a) = \frac{a}{\sigma^2} \cdot {\rm exp} [ -\frac{a^2 + |z_0|^2}{2\sigma^2}] \cdot {\rm I}_0 \left [ \frac{a \cdot |z_0|}{\sigma^2} \right ]\hspace{0.05cm}, \hspace{0.2cm}{\rm I }_0 (u) = | :$$f_a(a) = \frac{a}{\sigma^2} \cdot {\rm exp} [ -\frac{a^2 + |z_0|^2}{2\sigma^2}] \cdot {\rm I}_0 \left [ \frac{a \cdot |z_0|}{\sigma^2} \right ]\hspace{0.05cm}, \hspace{0.2cm}{\rm I }_0 (u) = | ||
\sum_{k = 0}^{\infty} \frac{ (u/2)^{2k}}{k! \cdot \Gamma (k+1)} | \sum_{k = 0}^{\infty} \frac{ (u/2)^{2k}}{k! \cdot \Gamma (k+1)} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | The graph shows the Rice PDF for $|z_0|^2 = 0,\ 2, \ 4, \ 10$ and $20$. For all curves, we have $\sigma = 1$ ⇒ $\sigma^2 = 1$. | |
| − | In | + | In this task, however, we will not consider the PDF of the magnitude, but the ACF of the complex factor $z(t)$, |
| − | + | $$\varphi_z ({\rm \Delta}t) = {\rm E}\big [ z(t) \cdot z^{\star}(t + {\rm \Delta}t)\big ] | |
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | + | and the corresponding power spectral density | |
:$${\it \Phi}_z (f_{\rm D}) | :$${\it \Phi}_z (f_{\rm D}) | ||
\hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.3cm} \varphi_z ({\rm \Delta}t) | \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.3cm} \varphi_z ({\rm \Delta}t) | ||
| Line 37: | Line 37: | ||
| − | '' | + | ''Notes:'' |
| − | * | + | * This task belongs to chapter [[Mobile_Kommunikation/Nichtfrequenzselektives_Fading_mit_Direktkomponente|Nichtfrequenzselektives Fading mit Direktkomponente]]. |
| − | * | + | * Reference is also made to the chapters [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)|Autokorrelationsfunktion (AKF)]] and [[Stochastische_Signaltheorie/Leistungsdichtespektrum_(LDS)|Leistungsdichtespektrum (LDS)]] in the book „Stochastic Signal Theory”. |
| − | === | + | ===Questionnaire== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which value of $|z_0|^2$ corresponds to Rayleigh fading? |
|type="{}"} | |type="{}"} | ||
| − | $|z_0|^2 \ = \ $ { 0. } $\ \rm $ | + | $|z_0|^2 \ = \ $ { 0. } $\ \ $rm $ |
| − | { | + | {Let $|z_0|^2 \ne 0$. Which of the following functions depend only on $|z_0|^2 = x_0^2$ + $y_0^2$ but not on its components $x_0^2$ and $y_0^2$ alone? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - PDF $f_x(x)$ of the real part, |
| − | - | + | - PDF $f_y(y)$ of the imaginary part, |
| − | + | + | + PDF $f_a(a)$ of the amount |
| − | - | + | - PDF $f_{\rm \phi}(\phi)$ of the phase, |
| − | + | + | + ACF $\varphi_z(\Delta t)$ the complex quantity $z(t)$, |
| − | + | + | + PSD ${\it \Phi}_z(f_{\rm D})$ the complex quantity $z(t)$. |
| − | { | + | {Calculate the root mean square value ${\rm E}\big[|z(t)|^2\big]$ for different values of $|z_0|^2$. Assume $\sigma^2 = 1$. |
|type="{}"} | |type="{}"} | ||
| − | $|z_0|^2 = 0\text{:} \hspace{0.52cm} {\rm E}\big[|z(t)|^2\big] \ = \ $ { 2 3% } $\ \rm $ | + | $|z_0|^2 = 0\text{:} \hspace{0.52cm} {\rm E}\big[|z(t)|^2\big] \ = \ $ { 2 3% } $\ \ \rm $ |
| − | $|z_0|^2 = 2\text{:} \hspace{0.52cm} {\rm E}\big[|z(t)|^2\big] \ = \ $ { 4 3% } $\ \rm $ | + | $|z_0|^2 = 2\text{:} \hspace{0.52cm} {\rm E}\big[|z(t)|^2\big] \ = \ $ { 4 3% } $\ \ \rm $ |
| − | $|z_0|^2 = 10\text{:} \hspace{0.3cm} {\rm E}\big[|z(t)|^2\big] \ = \ $ { 12 3% } $\ \rm $ | + | $|z_0|^2 = 10\text{:} \hspace{0.3cm} {\rm E}\big[|z(t)|^2\big] \ = \ $ { 12 3% } $\ \ \rm $ |
| − | { | + | {How do the autocorrelation functions (ACFs) of the black, the blue and the green channel differ? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The „blue” ACF is above the „black” ACF by about $4$ units. |
| − | + | - The „blue” ACF is below the „black” ACF by about $2$ units. | |
| − | + | - The „green” ACF is wider than the „blue” by the factor $2.5$ . | |
| − | { | + | {How do the power spectral densities (PSDs) differ among the black, blue, and green mobile radio channels? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The „black” PSD is purely continuous (no Dirac). |
| − | + | + | + The „blue” and „green” PSDs contain one Dirac each. |
| − | + | + | + The „green” Dirac has a greater weight than the „blue” one. |
</quiz> | </quiz> | ||
| − | === | + | ===Sample solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <i>Rayleigh fading</i> results from the <i>Rice fading</i> with $|z_0|^2 \ \underline {= \ 0}$. |
| − | '''(2)''' | + | '''(2)''' <u>Options 3, 5 and 6</u> are correct: |
| − | + | It is obvious that | |
| − | * $f_x(x)$ | + | * $f_x(x)$ depends on $x_0$ |
| − | * $f_y(y)$ | + | * $f_y(y)$ depends on $y_0$ |
| − | * $f_{\rm \phi}(\phi)$ | + | * $f_{\rm \phi}(\phi)$ depends on the ratio $y_0/x_0$. |
| − | + | The given equation for the PDF $f_a(a)$ shows that the magnitude $a$ depends only on $|z_0|$. | |
| − | + | For the ACF, using $z(t) = x(t) + {\rm j} \cdot y(t)$ we have | |
:$$\varphi_z ({\rm \Delta}t) = {\rm E}\left [ z(t) \cdot z^{\star}(t + {\rm \Delta}t)\right] = {\rm E}\left [ \left ( x(t) + {\rm j} \cdot y(t) \right )\cdot (x(t + {\rm \Delta}t) - {\rm j} \cdot (y(t+ {\rm \Delta}t)\right ] | :$$\varphi_z ({\rm \Delta}t) = {\rm E}\left [ z(t) \cdot z^{\star}(t + {\rm \Delta}t)\right] = {\rm E}\left [ \left ( x(t) + {\rm j} \cdot y(t) \right )\cdot (x(t + {\rm \Delta}t) - {\rm j} \cdot (y(t+ {\rm \Delta}t)\right ] | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | Because of the statistical independence between real and imaginary parts, the equation can be simplified as follows: | |
:$$\varphi_z ({\rm \Delta}t) = {\rm E}\left [ x(t) \cdot x(t + {\rm \Delta}t)\right ] + | :$$\varphi_z ({\rm \Delta}t) = {\rm E}\left [ x(t) \cdot x(t + {\rm \Delta}t)\right ] + | ||
{\rm E}\left [ y(t) \cdot y(t + {\rm \Delta}t)\right ] \hspace{0.05cm}.$$ | {\rm E}\left [ y(t) \cdot y(t + {\rm \Delta}t)\right ] \hspace{0.05cm}.$$ | ||
| − | + | With $x(t) = u(t) + x_0$ and $t' = t + \Delta t$, the first part results in $x(t) = u(t) + x_0$: | |
:$${\rm E}\left [ x(t) \cdot x(t')\right ] = {\rm E}\left [ u(t) \cdot u(t')\right ] + x_0 \cdot {\rm E}\left [ u(t) \right ] | :$${\rm E}\left [ x(t) \cdot x(t')\right ] = {\rm E}\left [ u(t) \cdot u(t')\right ] + x_0 \cdot {\rm E}\left [ u(t) \right ] | ||
+ x_0 \cdot {\rm E}\left [ u(t') \right ] + x_0^2\hspace{0.05cm},$$ | + x_0 \cdot {\rm E}\left [ u(t') \right ] + x_0^2\hspace{0.05cm},$$ | ||
| Line 108: | Line 108: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | This takes into account that the Gaussian random variable $u(t)$ has zero mean and has the variance $\sigma^2$. | |
| − | In | + | In the same way with $y(t) = \upsilon (t) + y_0$ is obtained: |
:$${\rm E}\left [ y(t) \cdot y(t + {\rm \Delta}t)\right ] = \ ... \ = \varphi_v ({\rm \Delta}t) + y_0^2 \hspace{0.3cm} | :$${\rm E}\left [ y(t) \cdot y(t + {\rm \Delta}t)\right ] = \ ... \ = \varphi_v ({\rm \Delta}t) + y_0^2 \hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm} \varphi_z ({\rm \Delta}t) = \varphi_u ({\rm \Delta}t) + \varphi_v ({\rm \Delta}t) + x_0^2 + y_0^2 | \Rightarrow \hspace{0.3cm} \varphi_z ({\rm \Delta}t) = \varphi_u ({\rm \Delta}t) + \varphi_v ({\rm \Delta}t) + x_0^2 + y_0^2 | ||
| Line 116: | Line 116: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | But if the ACF $\varphi_z(\Delta t)$ only depends on $|z_0^2|$, then this also applies to the Fourier transform „LDS”. | |
| − | '''(3)''' | + | '''(3)''' The root mean square can be calculated from the PDF of the magnitude: |
:$${\rm E}\left [ |z(t)|^2 \right ] = {\rm E}\left [ a^2 \right ] = \int_{0}^{\infty}a^2 \cdot f_a(a)\hspace{0.15cm}{\rm d}a | :$${\rm E}\left [ |z(t)|^2 \right ] = {\rm E}\left [ a^2 \right ] = \int_{0}^{\infty}a^2 \cdot f_a(a)\hspace{0.15cm}{\rm d}a | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | At the same time, the root mean square value – i.e. the power – is also determined by the AKF: | |
| − | + | $${\rm E}\left [ |z(t)|^2 \right ] = \varphi_z ({\rm \delta}t = 0) = 2 \cdot \varphi_u ({\rm \delta}t = 0) + |z_0|^2 = 2 \cdot \sigma^2 + |z_0|^2 | |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | With $\sigma = 1$ you get the following numerical results: | |
| − | :$$ | + | :$$ \ |z_0|^2 = 0\text{:} \ \hspace{0.3cm}{\rm E}\left [ |z(t)|^2 \right ] = 2 + 0 \hspace{0.15cm} \underline{ = 2} \hspace{0.05cm},$$ |
| − | :$$ | + | :$$ \ |z_0|^2 = 2\text{:} \ \hspace{0.3cm}{\rm E}\left [ |z(t)|^2 \right ] = 2 + 2 \hspace{0.15cm} \underline{ = 4} \hspace{0.05cm},$$ |
:$$|z_0|^2 = 10\text{:} \ \hspace{0.3cm}{\rm E}\left [ |z(t)|^2 \right ] = 2 + 10 \hspace{0.15cm} \underline{ = 12} \hspace{0.05cm}.$$ | :$$|z_0|^2 = 10\text{:} \ \hspace{0.3cm}{\rm E}\left [ |z(t)|^2 \right ] = 2 + 10 \hspace{0.15cm} \underline{ = 12} \hspace{0.05cm}.$$ | ||
| − | '''(4)''' | + | '''(4)''' Correct is the <u>solution 1</u>, as already derived in the sample solution for '''(2)'''. |
| − | + | The following statements would also be correct: | |
| − | * | + | * The „blue” AKF is 4 over the „black”. |
| − | * | + | * The „green” AKF is 6 over the „blue”. |
| − | '''(5)''' <u> | + | '''(5)''' <u>All solution suggestions apply</u>. |
| − | * | + | * The „black” LDS is a [[Mobile_Communication/Statistical_Bonds_within_Rayleigh%E2%80%93Process#AKF_and_LDS_with_Rayleigh.E2.80.93Fading|Jakes–Spectrum]] and therefore continuous, i.e. all frequencies are present within an interval. |
| − | * In | + | * In the autocorrelation function (AKF) of the blue or green channel, the constant $|z_0|^2$ also occurs. |
| − | * | + | * In the power density spectrum (LDS), there are Dirac functions in the GCF at the Doppler frequency $f_{\rm D} = 0$ with the weight $|z_0|^2$ because of these constants. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 11:33, 1 April 2020
One speaks of Rice fading if the complex factor describing the mobile radio channel contains $z(t)$ besides the purely stochastic component $x(t) +{\rm j} \cdot y(t)$ a deterministic part of the form $x_0 + {\rm j} \cdot y_0$ .
The equations of Rice fading can be summarized briefly as follows:
- $$r(t) = z(t) \cdot s(t) ,$$
- $$z(t) = x(t) + {\rm j} \cdot y(t) ,$$
- $$x(t) = u(t) + x_0 ,$$
- $$y(t) = v(t) + y_0 .$$
The following applies:
- The direct path is defined by the complex constant $z_0 = x_0 + {\rm j} \cdot y_0$ . The magnitude of this time-invariant component is
- $$|z_0| = \sqrt{x_0^2 + y_0^2}\hspace{0.05cm}.$$
- $u(t)$ and $v(t)$ are zero-mean Gaussian random processes, both with variance $\sigma^2$ and uncorrelated with each other. They model scattering, refraction; and diffraction effects on a variety of indirect paths.
- The magnitude $a(t) = |z(t)|$ has a Rice PDF, which gives this channel model its name. For $a ≥ 0$, the PDF is
- $$f_a(a) = \frac{a}{\sigma^2} \cdot {\rm exp} [ -\frac{a^2 + |z_0|^2}{2\sigma^2}] \cdot {\rm I}_0 \left [ \frac{a \cdot |z_0|}{\sigma^2} \right ]\hspace{0.05cm}, \hspace{0.2cm}{\rm I }_0 (u) = \sum_{k = 0}^{\infty} \frac{ (u/2)^{2k}}{k! \cdot \Gamma (k+1)} \hspace{0.05cm}.$$
The graph shows the Rice PDF for $|z_0|^2 = 0,\ 2, \ 4, \ 10$ and $20$. For all curves, we have $\sigma = 1$ ⇒ $\sigma^2 = 1$.
In this task, however, we will not consider the PDF of the magnitude, but the ACF of the complex factor $z(t)$,
$$\varphi_z ({\rm \Delta}t) = {\rm E}\big [ z(t) \cdot z^{\star}(t + {\rm \Delta}t)\big ]
\hspace{0.05cm},$$
and the corresponding power spectral density
- $${\it \Phi}_z (f_{\rm D}) \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.3cm} \varphi_z ({\rm \Delta}t) \hspace{0.05cm}.$$
Notes:
- This task belongs to chapter Nichtfrequenzselektives Fading mit Direktkomponente.
- Reference is also made to the chapters Autokorrelationsfunktion (AKF) and Leistungsdichtespektrum (LDS) in the book „Stochastic Signal Theory”.
=Questionnaire
Sample solution
(2) Options 3, 5 and 6 are correct:
It is obvious that
- $f_x(x)$ depends on $x_0$
- $f_y(y)$ depends on $y_0$
- $f_{\rm \phi}(\phi)$ depends on the ratio $y_0/x_0$.
The given equation for the PDF $f_a(a)$ shows that the magnitude $a$ depends only on $|z_0|$.
For the ACF, using $z(t) = x(t) + {\rm j} \cdot y(t)$ we have
- $$\varphi_z ({\rm \Delta}t) = {\rm E}\left [ z(t) \cdot z^{\star}(t + {\rm \Delta}t)\right] = {\rm E}\left [ \left ( x(t) + {\rm j} \cdot y(t) \right )\cdot (x(t + {\rm \Delta}t) - {\rm j} \cdot (y(t+ {\rm \Delta}t)\right ] \hspace{0.05cm}.$$
Because of the statistical independence between real and imaginary parts, the equation can be simplified as follows:
- $$\varphi_z ({\rm \Delta}t) = {\rm E}\left [ x(t) \cdot x(t + {\rm \Delta}t)\right ] + {\rm E}\left [ y(t) \cdot y(t + {\rm \Delta}t)\right ] \hspace{0.05cm}.$$
With $x(t) = u(t) + x_0$ and $t' = t + \Delta t$, the first part results in $x(t) = u(t) + x_0$:
- $${\rm E}\left [ x(t) \cdot x(t')\right ] = {\rm E}\left [ u(t) \cdot u(t')\right ] + x_0 \cdot {\rm E}\left [ u(t) \right ] + x_0 \cdot {\rm E}\left [ u(t') \right ] + x_0^2\hspace{0.05cm},$$
- $$\Rightarrow \hspace{0.3cm} {\rm E}\left [ x(t) \cdot x(t + {\rm \Delta}t)\right ] = {\rm E}\left [ u(t) \cdot u(t + {\rm \Delta}t)\right ] + x_0^2 = \varphi_u ({\rm \Delta}t) + x_0^2 \hspace{0.05cm}.$$
This takes into account that the Gaussian random variable $u(t)$ has zero mean and has the variance $\sigma^2$.
In the same way with $y(t) = \upsilon (t) + y_0$ is obtained:
- $${\rm E}\left [ y(t) \cdot y(t + {\rm \Delta}t)\right ] = \ ... \ = \varphi_v ({\rm \Delta}t) + y_0^2 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \varphi_z ({\rm \Delta}t) = \varphi_u ({\rm \Delta}t) + \varphi_v ({\rm \Delta}t) + x_0^2 + y_0^2 = 2 \cdot \varphi_u ({\rm \Delta}t) + |z_0|^2 \hspace{0.05cm}.$$
But if the ACF $\varphi_z(\Delta t)$ only depends on $|z_0^2|$, then this also applies to the Fourier transform „LDS”.
(3) The root mean square can be calculated from the PDF of the magnitude:
- $${\rm E}\left [ |z(t)|^2 \right ] = {\rm E}\left [ a^2 \right ] = \int_{0}^{\infty}a^2 \cdot f_a(a)\hspace{0.15cm}{\rm d}a \hspace{0.05cm}.$$
At the same time, the root mean square value – i.e. the power – is also determined by the AKF: $${\rm E}\left [ |z(t)|^2 \right ] = \varphi_z ({\rm \delta}t = 0) = 2 \cdot \varphi_u ({\rm \delta}t = 0) + |z_0|^2 = 2 \cdot \sigma^2 + |z_0|^2 \hspace{0.05cm}.$$
With $\sigma = 1$ you get the following numerical results:
- $$ \ |z_0|^2 = 0\text{:} \ \hspace{0.3cm}{\rm E}\left [ |z(t)|^2 \right ] = 2 + 0 \hspace{0.15cm} \underline{ = 2} \hspace{0.05cm},$$
- $$ \ |z_0|^2 = 2\text{:} \ \hspace{0.3cm}{\rm E}\left [ |z(t)|^2 \right ] = 2 + 2 \hspace{0.15cm} \underline{ = 4} \hspace{0.05cm},$$
- $$|z_0|^2 = 10\text{:} \ \hspace{0.3cm}{\rm E}\left [ |z(t)|^2 \right ] = 2 + 10 \hspace{0.15cm} \underline{ = 12} \hspace{0.05cm}.$$
(4) Correct is the solution 1, as already derived in the sample solution for (2).
The following statements would also be correct:
- The „blue” AKF is 4 over the „black”.
- The „green” AKF is 6 over the „blue”.
(5) All solution suggestions apply.
- The „black” LDS is a Jakes–Spectrum and therefore continuous, i.e. all frequencies are present within an interval.
- In the autocorrelation function (AKF) of the blue or green channel, the constant $|z_0|^2$ also occurs.
- In the power density spectrum (LDS), there are Dirac functions in the GCF at the Doppler frequency $f_{\rm D} = 0$ with the weight $|z_0|^2$ because of these constants.