Difference between revisions of "Aufgaben:Exercise 1.6: Cyclic Redundancy Check"
| Line 75: | Line 75: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Aufgrund des größten Zählerexponenten ( | + | '''(1)''' Richtig ist <u>der Lösungsvorschlag 2</u>: |
| − | :$$E(D) \cdot G(D) \ = \ (D^7+ D^5+D^3+1)\cdot (D^4+ D+1) \ = | + | *Aufgrund des größten Zählerexponenten $(D^{11})$ und des höchsten Nennerexponenten ($(D^{4})$) kann der erste Vorschlag $E(D) = D^{5} + D^{3} + 1$ als Ergebnis ausgeschlossen werden ⇒ $(D) = D^{7} + D^{5} + D^{3} + 1$. |
| − | + | ||
| − | + | ||
| − | Zu berücksichtigen ist hierbei, dass bei Modulo–2–Rechnungen $D^{4} + D^{4} = 0$ gilt. Damit ergibt sich der folgende Rest: | + | *Die Modulo–2–Multiplikation von $E(D)$ mit dem Generatorpolynom $G(D) = D^{4} + D + 1$ liefert: |
| + | :$$E(D) \cdot G(D) \ = \ (D^7+ D^5+D^3+1)\cdot (D^4+ D+1) \ = D^{11}+D^8+D^7+D^9+D^6+D^5+D^7+D^4+D^3+D^4+ D+1 \hspace{0.05cm}.$$ | ||
| + | *Zu berücksichtigen ist hierbei, dass bei Modulo–2–Rechnungen $D^{4} + D^{4} = 0$ gilt. Damit ergibt sich der folgende Rest: | ||
:$$R(D) = D^{11}+D^9+D^8+D^6+D^5- E(D) \cdot G(D) = D^3+D+1 \hspace{0.05cm}.$$ | :$$R(D) = D^{11}+D^9+D^8+D^6+D^5- E(D) \cdot G(D) = D^3+D+1 \hspace{0.05cm}.$$ | ||
| − | |||
| − | + | [[File:P_ID1628__Bei_A_1_6b.png|right|frame|Registerbelegungen bei CRC4]] | |
| − | Aus dem Ergebnis der | + | '''(2)''' Aus dem Ergebnis der Teilaufgabe (1) folgt: |
| − | :$${\rm CRC0 = 1},\hspace{0.2cm}{\rm CRC1 = 1}, | + | :$${\rm CRC0 = 1},\hspace{0.2cm}{\rm CRC1 = 1},\hspace{0.2cm}{\rm CRC2 = 0},\hspace{0.2cm}{\rm CRC3 = 1}\hspace{0.05cm}.$$ |
| − | |||
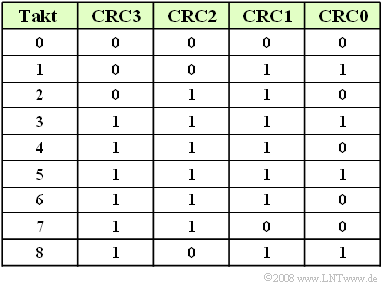
Die Tabelle zeigt einen zweiten Lösungsweg auf: Sie enthält die Registerbelegungen der gegebenen Schaltung zu den Taktzeiten 0, ... , 8. | Die Tabelle zeigt einen zweiten Lösungsweg auf: Sie enthält die Registerbelegungen der gegebenen Schaltung zu den Taktzeiten 0, ... , 8. | ||
| + | <br clear=all> | ||
| + | '''(3)''' Richtig ist nur der <u>Lösungsvorschlag 2</u>.: | ||
| + | *Der Empfänger teilt das Polynom $P(D)$ der Empfangsfolge durch das Generatorpolynom $G(D)$. | ||
| + | *Liefert diese Modulo–2–Division den Rest $R(D) = 0$, so wurden alle 12 Bit richtig übertragen. | ||
| + | *Dies trifft für den zweiten Lösungsvorschlag zu, wie ein Vergleich mit den Teilaufgaben (1) und (2) zeigt. Es gilt ohne Rest: | ||
| + | :$$(D^{11}+D^9+D^8+D^6+D^5+D^3+D+1) : (D^4+ D+1)= D^7+D^5+D^3+1 \hspace{0.05cm}.$$ | ||
| + | *Bei Lösungsvorschlag 1 wurde das 6. Informationsbit verfälscht, beim Lösungsvorschlag 3 das CRC1–Bit. | ||
| − | |||
| − | |||
| − | |||
| − | '''(4)''' Die | + | '''(4)''' Richtig sind <u>die Lösungsvorschläge 1 und 3</u>: |
| − | + | *Die Grafik verdeutlicht die Modulo–2–Divisionen für die drei angegebenen Empfangsfolgen in vereinfachter Form (mit Nullen und Einsen). | |
| − | In ausgeschriebener Form lauten die Polynomdivisionen: | + | *Man erkennt, dass nur bei der Folge 2 die Division ohne Rest möglich ist. |
| + | *In ausgeschriebener Form lauten die Polynomdivisionen: | ||
:$$\ (1) \ \hspace{0.2cm}(D^6+D^5+D^4+1) : (D^4+ D+1)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Rest}\hspace{0.15cm}D^3+ D+1\hspace{0.05cm},$$ | :$$\ (1) \ \hspace{0.2cm}(D^6+D^5+D^4+1) : (D^4+ D+1)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Rest}\hspace{0.15cm}D^3+ D+1\hspace{0.05cm},$$ | ||
:$$\ (2) \ \hspace{0.2cm}(D^7+D^6+D^5+D^4+1) : (D^4+ D+1)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm ohne \hspace{0.15cm}Rest}\hspace{0.05cm},$$ | :$$\ (2) \ \hspace{0.2cm}(D^7+D^6+D^5+D^4+1) : (D^4+ D+1)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm ohne \hspace{0.15cm}Rest}\hspace{0.05cm},$$ | ||
:$$\ (3) \ \hspace{0.2cm}(D^7+D^6+D^5+D^4+D^3+1) : (D^4+ D+1) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Rest}\hspace{0.15cm}D^3\hspace{0.05cm}.$$ | :$$\ (3) \ \hspace{0.2cm}(D^7+D^6+D^5+D^4+D^3+1) : (D^4+ D+1) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Rest}\hspace{0.15cm}D^3\hspace{0.05cm}.$$ | ||
| + | [[File:P_ID1629__Bei_A_1_6d.png|center|frame|Polynomdivision der drei Empfangsfolgen]] | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 17:14, 19 December 2017
Die Synchronisation geschieht beim Primärmultiplexanschluss jeweils im Kanal $0$ – dem Synchronisationskanal – eines jeden Rahmens:
- Bei ungeraden Zeitrahmen (Nummer 1, 3, ... , 15) überträgt dieser das so genannte „Rahmenkennwort” mit dem festen Bitmuster X001 1011.
- Jeder gerade Rahmen (mit Nummer 2, 4, ... , 16) beinhaltet dagegen das „Meldewort” X1DN YYYY.
- Über das D–Bit und das N–Bit werden Fehlermeldungen signalisiert und die vier Y–Bits sind für Service–Funktionen reserviert.
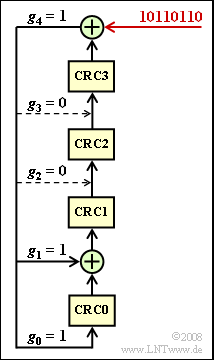
Das X–Bit wird jeweils durch das CRC4–Verfahren gewonnen, dessen Realisierung in der Grafik dargestellt ist:
- Aus jeweils acht Eingangsbits – in der gesamten Aufgabe wird hierfür die Bitfolge 1011 0110 angenommen – werden durch Modulo–2–Additionen und Verschiebungen die vier Prüfbits $\rm CRC3$, ... , $\rm CRC0$ gewonnen, die dem Eingangswort in dieser Reihenfolge hinzugefügt werden.
- Bevor das erste Bit in das Register geschoben wird, sind alle Register mit Nullen belegt:
- $${\rm CRC3 = CRC2 =CRC1 =CRC0 = 0}\hspace{0.05cm}.$$
- Nach 8 Schiebetakten steht in den vier Registern $\rm CRC3$, ... , $\rm CRC0$ die CRC4–Prüfsumme.
Die Anzapfungen des Schieberegisters sind $g_{0} = 1, g_{1} = 1, g_{2} = 0, g_{3} = 0$ und $g_{4} = 1$.
- Das dazugehörige Generatorpolynom lautet:
- $$G(D) = D^4 + D +1 \hspace{0.05cm}.$$
- Die sendeseitige CRC4–Prüfsumme erhält man auch als Rest der Polynomdivision
- $$(D^{11} +D^{9} +D^{8}+D^{6}+D^{5})/G(D) \hspace{0.05cm}.$$
- Das Divisorpolynom ergibt sich aus der Eingangsfolge und vier angehängten Nullen: 1011 0110 0000.
Auch die CRC4–Überprüfung beim Empfänger entsprechend Teilaufgabe (4) kann durch eine Polynomdivision dargestellt werden. Sie lässt sich durch eine Schieberegisterstruktur in ähnlicher Weise realisieren wie die sendeseitige Gewinnung der CRC4–Prüfsumme.
Hinweise:
- Die Aufgabe gehört zum Kapitel ISDN–Primärmultiplexanschluss .
- Zur Lösung der Aufgabe werden einige Grundkenntnisse der Kanalcodierung vorausgesetzt.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
(1) Richtig ist der Lösungsvorschlag 2:
- Aufgrund des größten Zählerexponenten $(D^{11})$ und des höchsten Nennerexponenten ($(D^{4})$) kann der erste Vorschlag $E(D) = D^{5} + D^{3} + 1$ als Ergebnis ausgeschlossen werden ⇒ $(D) = D^{7} + D^{5} + D^{3} + 1$.
- Die Modulo–2–Multiplikation von $E(D)$ mit dem Generatorpolynom $G(D) = D^{4} + D + 1$ liefert:
- $$E(D) \cdot G(D) \ = \ (D^7+ D^5+D^3+1)\cdot (D^4+ D+1) \ = D^{11}+D^8+D^7+D^9+D^6+D^5+D^7+D^4+D^3+D^4+ D+1 \hspace{0.05cm}.$$
- Zu berücksichtigen ist hierbei, dass bei Modulo–2–Rechnungen $D^{4} + D^{4} = 0$ gilt. Damit ergibt sich der folgende Rest:
- $$R(D) = D^{11}+D^9+D^8+D^6+D^5- E(D) \cdot G(D) = D^3+D+1 \hspace{0.05cm}.$$
(2) Aus dem Ergebnis der Teilaufgabe (1) folgt:
- $${\rm CRC0 = 1},\hspace{0.2cm}{\rm CRC1 = 1},\hspace{0.2cm}{\rm CRC2 = 0},\hspace{0.2cm}{\rm CRC3 = 1}\hspace{0.05cm}.$$
Die Tabelle zeigt einen zweiten Lösungsweg auf: Sie enthält die Registerbelegungen der gegebenen Schaltung zu den Taktzeiten 0, ... , 8.
(3) Richtig ist nur der Lösungsvorschlag 2.:
- Der Empfänger teilt das Polynom $P(D)$ der Empfangsfolge durch das Generatorpolynom $G(D)$.
- Liefert diese Modulo–2–Division den Rest $R(D) = 0$, so wurden alle 12 Bit richtig übertragen.
- Dies trifft für den zweiten Lösungsvorschlag zu, wie ein Vergleich mit den Teilaufgaben (1) und (2) zeigt. Es gilt ohne Rest:
- $$(D^{11}+D^9+D^8+D^6+D^5+D^3+D+1) : (D^4+ D+1)= D^7+D^5+D^3+1 \hspace{0.05cm}.$$
- Bei Lösungsvorschlag 1 wurde das 6. Informationsbit verfälscht, beim Lösungsvorschlag 3 das CRC1–Bit.
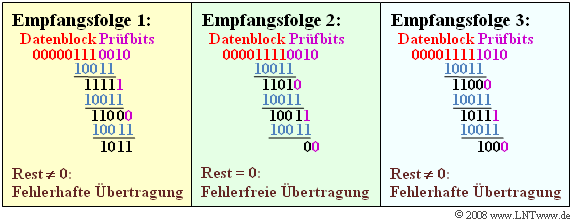
(4) Richtig sind die Lösungsvorschläge 1 und 3:
- Die Grafik verdeutlicht die Modulo–2–Divisionen für die drei angegebenen Empfangsfolgen in vereinfachter Form (mit Nullen und Einsen).
- Man erkennt, dass nur bei der Folge 2 die Division ohne Rest möglich ist.
- In ausgeschriebener Form lauten die Polynomdivisionen:
- $$\ (1) \ \hspace{0.2cm}(D^6+D^5+D^4+1) : (D^4+ D+1)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Rest}\hspace{0.15cm}D^3+ D+1\hspace{0.05cm},$$
- $$\ (2) \ \hspace{0.2cm}(D^7+D^6+D^5+D^4+1) : (D^4+ D+1)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm ohne \hspace{0.15cm}Rest}\hspace{0.05cm},$$
- $$\ (3) \ \hspace{0.2cm}(D^7+D^6+D^5+D^4+D^3+1) : (D^4+ D+1) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Rest}\hspace{0.15cm}D^3\hspace{0.05cm}.$$