Exercise 1.7: Entropy of Natural Texts
In the early 1950s, Claude E. Shannon estimated the entropy $H$ of the English language at one bit per character. A short time later, Karl Küpfmüller arrived at an entropy value of $H =1.3\ \rm bit/character$, i.e. a somewhat larger value, in an empirical study of the German language. Interestingly, the results of Shannon and Küpfmüller are based on two completely different methods.
The differing results cannot be explained by the small differences in the range of symbols $M$ :
- Shannon assumed $26$ letters and the space ⇒ $M = 27$.
- Küpfmüller assumed only $M = 26$ letters (i.e. without the space).
Both made no distinction between upper and lower case.
This task is intended to show how
- Erasures ⇒ one knows the location of an error, resp.
- Errors ⇒ it is not clear to the reader what is wrong and what is right,
have an effect on the comprehensibility of a text. Our text also contains the typical German letters "ä", "ö", "ü" and "ß" as well as numbers and punctuation. In addition, a distinction is made between upper and lower case.
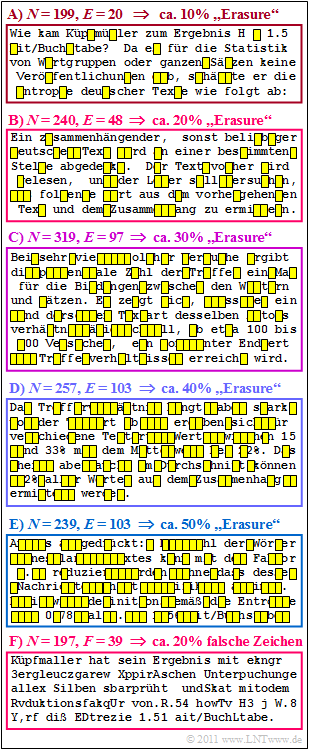
In the figure, a text dealing with Küpfmüller's approach is divided into six blocks of length between $N = 197$ and $N = 319$ aufgeteilt. Described is the check of his first analysis in a completely different way, which led to the result $H =1.51\ \rm bit/character$ .
- In the upper five blocks one recognises "Erasures" with different erasure probabilities between $10\%$ and $50\%$.
- In the last block, "character errors" with $20$–error probability are inserted.
The influence of such character errors on the readability of a text is to be compared in subtask (4) with the second block (outlined in red), for which the probability of an erasure is also $20\%$ .
Hints:
- The task belongs to the chapter Natural Discrete Sources.
- Bezug genommen wird insbesondere auf die beiden Seiten
- For the relative redundancy of a sequence, with the decision content $H_0$ and the entropy $H$ , applies
- $$r = \frac{H_0 - H}{H_0}\hspace{0.05cm}.$$
Questions
Musterlösung
Bei dem vorgegebenen deutschen Text dieser Aufgabe ist der Symbolumfang deutlich größer,
- da hier auch die typisch deutschen Zeichen "ä", "ö", "ü" und "ß" vorkommen,
- zwischen Klein– und Großschreibung unterschieden wird,
- und zudem noch Ziffern und Interpunktionszeichen hinzukommen.
(2) Mit dem Entscheidungsgehalt $H_0 = \log_2 \ (31) \approx 4.7 \ \rm bit/Zeichen$ und der Entropie $H = 1.3\ \rm bit/Zeichen $ erhält man für die relative Redundanz:
- $$r = \frac{H_0 - H}{H_0}= \frac{4.7 - 1.3}{4.7}\underline {\hspace{0.1cm}\approx 72.3\,\%}\hspace{0.05cm}.$$
(3) Richtig ist nur der erste Lösungsvorschlag:
- Laut Küpfmüller benötigt man nur $1.3$ Binärzeichen pro Quellenzeichen.
- Bei einer Datei der Länge $N$ würden also $1.3 \cdot N$ Binärsymbole ausreichen, allerdings nur dann, wenn die Quellensymbolfolge unendlich lang ist $(N \to \infty)$ und diese bestmöglich codiert wurde.
- Dagegen besagt Küpfmüllers Ergebnis und die in der Teilaufgabe (2) errechnete relative Redundanz von mehr als $70\%$ nicht, dass ein Leser den Text noch verstehen kann, wenn $70\%$ der Zeichen ausgelöscht wurden.
- Ein solcher Text ist weder unendlich lang, noch wurde er vorher optimal codiert.
(4) Richtig ist die Aussage 2:
- Testen Sie es selbst: Der zweite Block der Grafik auf der Angabenseite ist leichter zu entschlüsseln als der letzte Block, weil man weiß, wo Fehler sind.
- Wenn Sie es weiter versuchen wollen: Für den unteren Block (F) wurde genau die gleiche Zeichenfehlerfolge wie für Block (B) verwendet, das heißt, Fehler gibt es bei den Zeichen $6$, $35$, $37$, usw..
Abschließend wird der Originaltext angegeben, der auf der Angabenseite nur durch Auslöschungen (Erasures) oder echte Zeichenfehler verfälscht wiedergegeben ist.