Difference between revisions of "Aufgaben:Exercise 1.7: System Efficiencies"
m (Text replacement - "”" to """) |
|||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Optimization_of_Baseband_Transmission_Systems |
}} | }} | ||
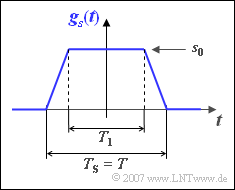
| − | [[File:P_ID1294__Dig_A_1_7.png|right|frame| | + | [[File:P_ID1294__Dig_A_1_7.png|right|frame|Basic transmission pulse "trapezoid" ]] |
| − | + | The receiver of a binary message transmission system with symbol duration $T$ consists of an integrator, which is represented by the impulse response | |
:$$h_{\rm E}(t) = \left\{ \begin{array}{c} 1/T \\ | :$$h_{\rm E}(t) = \left\{ \begin{array}{c} 1/T \\ | ||
0 \\ \end{array} \right.\quad | 0 \\ \end{array} \right.\quad | ||
| − | \begin{array}{*{1}c} {\rm{ | + | \begin{array}{*{1}c} {\rm{for}} |
| − | \\ {\rm{ | + | \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} |
\hspace{0.05cm}|t| < T/2 \hspace{0.05cm}, \\ | \hspace{0.05cm}|t| < T/2 \hspace{0.05cm}, \\ | ||
|t| > T/2 \\ | |t| > T/2 \\ | ||
\end{array}$$ | \end{array}$$ | ||
| − | + | This is followed by a threshold decision with optimal parameters. | |
| − | + | The basic transmission pulse $g_{s}(t)$ according to the diagram is generally trapezoidal and is parameterized by the time $T_{1}$: | |
| − | * | + | *For $T_{1} = 0$ the result is a triangular pulse, for $T_{1} = T$ the NRZ rectangle. |
| − | * | + | *The absolute pulse duration $T_{\rm S}$ is always equal to the symbol duration $T$, i.e. the distance between two transmission pulses. |
| − | + | The signal-to-noise power ratio (SNR) before the threshold decision can be calculated as follows, assuming no intersymbol interfering: | |
:$$\rho_d = {g_0^2}/{\sigma_d^2}\hspace{0.05cm}.$$ | :$$\rho_d = {g_0^2}/{\sigma_d^2}\hspace{0.05cm}.$$ | ||
| − | + | Here, $g_{0} = g_{d}(t = 0)$ is the maximum value of the basic transmitter pulse and | |
:$$\sigma_d^2 = {N_0}/{2} \cdot \int_{-\infty}^{+\infty}|h_{\rm E}(t)|^2 \,{\rm d} t = \frac{N_0}{2 \cdot T}$$ | :$$\sigma_d^2 = {N_0}/{2} \cdot \int_{-\infty}^{+\infty}|h_{\rm E}(t)|^2 \,{\rm d} t = \frac{N_0}{2 \cdot T}$$ | ||
| − | + | the noise power after the receiver filter in the presence of AWGN noise at its input. | |
| − | + | In the course of this exercise, the following quantities will be used: | |
| − | *$\rho_{d,\rm\hspace{0.05cm} max | L}$ | + | *$\rho_{d,\rm\hspace{0.05cm} max | L}$ is the maximum SNR under the constraint of power limitation. |
| − | *$\rho_{d,\rm\hspace{0.05cm} max | A}$ | + | *$\rho_{d,\rm\hspace{0.05cm} max | A}$ is the maximum SNR under peak limitation (amplitude limitation). |
| − | + | These definitions can be used to specify the system efficiencies: | |
:$$\eta_{\rm L} = \ \frac{\rho_d}{\rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm}|\hspace{0.05cm} | :$$\eta_{\rm L} = \ \frac{\rho_d}{\rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm}|\hspace{0.05cm} | ||
L}}}\hspace{0.05cm},$$ | L}}}\hspace{0.05cm},$$ | ||
| Line 37: | Line 37: | ||
\hspace{0.05cm} A}}} = {1}/{C_{\rm S}^2}\cdot \eta_{\rm L} \hspace{0.05cm}.$$ | \hspace{0.05cm} A}}} = {1}/{C_{\rm S}^2}\cdot \eta_{\rm L} \hspace{0.05cm}.$$ | ||
| − | + | Here, the ''crest factor'' $C_{\rm S}$ denotes the ratio between the maximum value and the rms value (root of power) of the transmitted signal $s(t)$. | |
| Line 44: | Line 44: | ||
| − | '' | + | ''Notes:'' |
| − | * | + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Optimization_of_Baseband_Transmission_Systems|Optimization of Baseband Transmission Systems]]. |
| − | * | + | *Use the following numerical values to solve the exercise: |
:$$s_0^2 = 10\,{\rm mW},\hspace{0.2cm}T = 3\,{\rm{ µ s}}, \hspace{0.2cm}N_0 = 3 \cdot 10^{-10}\,{\rm W/Hz}\hspace{0.05cm}.$$ | :$$s_0^2 = 10\,{\rm mW},\hspace{0.2cm}T = 3\,{\rm{ µ s}}, \hspace{0.2cm}N_0 = 3 \cdot 10^{-10}\,{\rm W/Hz}\hspace{0.05cm}.$$ | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the pulse energy $E_{\rm B}$ as a function of $T_{1}$. What are the values for $T_{1} = 0$ , $T_{1} = T/2$ and $T_{1} = T$? |
|type="{}"} | |type="{}"} | ||
$T_{1} = 0\text{:} \hspace{0.75cm} E_{\rm B} \ = \ $ { 1 3% } $\ \cdot 10^{-8} \, \rm Ws$ | $T_{1} = 0\text{:} \hspace{0.75cm} E_{\rm B} \ = \ $ { 1 3% } $\ \cdot 10^{-8} \, \rm Ws$ | ||
| Line 62: | Line 62: | ||
$T_{1} = T\text{:}\hspace{0.65cm} E_{\rm B} \ = \ $ { 3 3% } $\ \cdot 10^{-8} \, \rm Ws$ | $T_{1} = T\text{:}\hspace{0.65cm} E_{\rm B} \ = \ $ { 3 3% } $\ \cdot 10^{-8} \, \rm Ws$ | ||
| − | { | + | {What value $T_{1}$ leads to the maximum possible SNR when power is limited? |
|type="{}"} | |type="{}"} | ||
$T_{1}/T \ = \ $ { 1 3% } | $T_{1}/T \ = \ $ { 1 3% } | ||
| − | { | + | {Therefore, what is the maximum SNR with power limitation? |
|type="{}"} | |type="{}"} | ||
$\rho_{d,\hspace{0.05cm}\rm max \hspace{0.05cm}|\hspace{0.05cm} L} \ = \ $ { 200 3% } | $\rho_{d,\hspace{0.05cm}\rm max \hspace{0.05cm}|\hspace{0.05cm} L} \ = \ $ { 200 3% } | ||
| − | { | + | {How large is the basic transmitter pulse $g_{d}(t)$ in pulse center for $T_{1} = T/2$? |
|type="{}"} | |type="{}"} | ||
$g_{0} \ = \ $ { 0.075 3% } $\ \rm \sqrt{W}$ | $g_{0} \ = \ $ { 0.075 3% } $\ \rm \sqrt{W}$ | ||
| − | { | + | {Calculate the system efficiency $\eta_{\rm L}$ when power is limited $(T_{1} = T/2)$. |
|type="{}"} | |type="{}"} | ||
$\eta_{\rm L} \ = \ $ { 0.5625 3% } | $\eta_{\rm L} \ = \ $ { 0.5625 3% } | ||
| − | { | + | {Calculate the crest factor $(T_{1} = T/2)$. |
|type="{}"} | |type="{}"} | ||
$C_{\rm S} \ = \ $ { 1.225 3% } | $C_{\rm S} \ = \ $ { 1.225 3% } | ||
| − | { | + | {Calculate the system efficiency at peak limitation $(T_{1} = T/2)$. |
|type="{}"} | |type="{}"} | ||
$\eta_{\rm A} \ = \ $ { 0.375 3% } | $\eta_{\rm A} \ = \ $ { 0.375 3% } | ||
| Line 91: | Line 91: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' To simplify the calculations, we set $T_1' = T_1/2$ and $T_2' = (T – T_1)/2$. |
| − | * | + | *This gives for the transmitted pulse energy: |
:$$E_{\rm B} = | :$$E_{\rm B} = | ||
\int_{-\infty}^{+\infty}g_s^2(t) \,{\rm d} t = | \int_{-\infty}^{+\infty}g_s^2(t) \,{\rm d} t = | ||
| Line 100: | Line 100: | ||
t\hspace{0.2cm}+ \hspace{0.2cm}2 \cdot \int_{T_1\hspace{0.0cm}'}^{T/2}g_s^2(t) \,{\rm d} t | t\hspace{0.2cm}+ \hspace{0.2cm}2 \cdot \int_{T_1\hspace{0.0cm}'}^{T/2}g_s^2(t) \,{\rm d} t | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *According to this division, it can also be written: |
:$${E_{\rm B}}/{2} = s_0^2 \cdot T_1\hspace{0.0cm}' + E_2 | :$${E_{\rm B}}/{2} = s_0^2 \cdot T_1\hspace{0.0cm}' + E_2 | ||
| − | \hspace{0.05cm},\hspace{0.3cm}{\rm | + | \hspace{0.05cm},\hspace{0.3cm}{\rm with}\hspace{0.3cm} |
E_{\rm 2} = \ | E_{\rm 2} = \ | ||
\int_{T_1\hspace{0.0cm}'}^{T/2}g_s^2(t) \,{\rm d} t | \int_{T_1\hspace{0.0cm}'}^{T/2}g_s^2(t) \,{\rm d} t | ||
| Line 114: | Line 114: | ||
\cdot\frac {T_2\hspace{0.0cm}'\hspace{0.02cm}}{3} | \cdot\frac {T_2\hspace{0.0cm}'\hspace{0.02cm}}{3} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *Substituted into the above equation one obtains: |
:$${E_{\rm B}}/{2} = s_0^2 \cdot \frac {T_1}{2}+ s_0^2 \cdot \frac {T-T_1}{2 \cdot | :$${E_{\rm B}}/{2} = s_0^2 \cdot \frac {T_1}{2}+ s_0^2 \cdot \frac {T-T_1}{2 \cdot | ||
3}= s_0^2 \cdot \left [\frac{T}{6} + \frac{T_1}{3}\right ]\hspace{0.3cm} | 3}= s_0^2 \cdot \left [\frac{T}{6} + \frac{T_1}{3}\right ]\hspace{0.3cm} | ||
\hspace{0.3cm}\Rightarrow E_{\rm B} = {s_0^2}/{3}\cdot \left (T + 2 \cdot T_1 \right )\hspace{0.05cm}.$$ | \hspace{0.3cm}\Rightarrow E_{\rm B} = {s_0^2}/{3}\cdot \left (T + 2 \cdot T_1 \right )\hspace{0.05cm}.$$ | ||
| − | * | + | *With the given values ${s_{0}}^{2} = 10 \ \rm mW$ and $T = 3\ \rm µ s$ we obtain: |
:$$T_1 = 0\text{:} \hspace{0.75cm} {E_{\rm B}} = \ 1/3 \cdot{s_0^2 \cdot T}= 1/3 \cdot {10^{-2}\,{\rm W} \cdot 3 \cdot 10^{-6}\,{\rm s}} \hspace{0.1cm}\underline {= 1 \cdot 10^{-8}\,{\rm | :$$T_1 = 0\text{:} \hspace{0.75cm} {E_{\rm B}} = \ 1/3 \cdot{s_0^2 \cdot T}= 1/3 \cdot {10^{-2}\,{\rm W} \cdot 3 \cdot 10^{-6}\,{\rm s}} \hspace{0.1cm}\underline {= 1 \cdot 10^{-8}\,{\rm | ||
Ws}}\hspace{0.05cm},$$ | Ws}}\hspace{0.05cm},$$ | ||
| Line 127: | Line 127: | ||
| − | '''(2)''' | + | '''(2)''' The system efficiency under power limitation is maximum $(\eta_{\rm L} = 1)$, when the basic transmission pulse $g_{s}(t)$ has the same shape as the impulse response $h_{\rm E}(t)$. This is true here for the NRZ transmitted pulse: $T_1/T \ \underline{= 1}$. |
| − | '''(3)''' | + | '''(3)''' Under the condition given in question '''(2)''', the maximum SNR is obtained: |
:$$\rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm}| \hspace{0.05cm} | :$$\rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm}| \hspace{0.05cm} | ||
L}}= \frac{2 \cdot E_{\rm B}}{N_0} = \frac{2 \cdot 3 \cdot 10^{-8}\,{\rm Ws}}{3 \cdot 10^{-10}\,{\rm | L}}= \frac{2 \cdot E_{\rm B}}{N_0} = \frac{2 \cdot 3 \cdot 10^{-8}\,{\rm Ws}}{3 \cdot 10^{-10}\,{\rm | ||
| Line 136: | Line 136: | ||
| − | '''(4)''' | + | '''(4)''' In general, $g_{d}(t) = g_{s}(t) ∗ h_{\rm E}(t)$. For $t = 0$, $T_1 = T/2$ gives the trapezoidal area for this: |
:$$g_0 = g_d(t=0) = \frac{1}{T} \cdot \int_{-\infty}^{+\infty}g_s(t) \,{\rm d} t = \frac{T + T_1}{2} \cdot s_0 = 0.75 \cdot 0.1 \cdot \sqrt{\rm W} \hspace{0.1cm}\underline {= 0.075 \,\sqrt{\rm W}} \hspace{0.05cm}.$$ | :$$g_0 = g_d(t=0) = \frac{1}{T} \cdot \int_{-\infty}^{+\infty}g_s(t) \,{\rm d} t = \frac{T + T_1}{2} \cdot s_0 = 0.75 \cdot 0.1 \cdot \sqrt{\rm W} \hspace{0.1cm}\underline {= 0.075 \,\sqrt{\rm W}} \hspace{0.05cm}.$$ | ||
| − | '''(5)''' | + | '''(5)''' With $T_1 = T/2$ (trapezoidal transmitted pulses), we obtain for the signal-to-noise ratio: |
| − | :$$\rho_d = \frac{g_0^2}{\sigma_d^2}\hspace{0.3cm}{\rm | + | :$$\rho_d = \frac{g_0^2}{\sigma_d^2}\hspace{0.3cm}{\rm with}\hspace{0.3cm} g_0^2=0.075^2\, {\rm W},\hspace{0.1cm} \sigma_d^2 = \frac{N_0}{2 \cdot T} = 5 \cdot 10^{-5}\,{\rm W}\hspace{0.3cm} |
\Rightarrow \hspace{0.3cm}\rho_d = \frac{0.075^2\, {\rm W}}{5 \cdot 10^{-5}\,{\rm W}} = 112.5 \hspace{0.05cm}.$$ | \Rightarrow \hspace{0.3cm}\rho_d = \frac{0.075^2\, {\rm W}}{5 \cdot 10^{-5}\,{\rm W}} = 112.5 \hspace{0.05cm}.$$ | ||
| − | * | + | *Thus, the system efficiency under power limitation with the result of '''(3)''': |
:$$\eta_{\rm L} = \frac{\rho_d}{\rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm} | \hspace{0.05cm} L}}}= \frac{112.5}{200}\hspace{0.1cm}\underline {= 0.5625 }\hspace{0.05cm}.$$ | :$$\eta_{\rm L} = \frac{\rho_d}{\rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm} | \hspace{0.05cm} L}}}= \frac{112.5}{200}\hspace{0.1cm}\underline {= 0.5625 }\hspace{0.05cm}.$$ | ||
| − | * | + | *Due to the mismatch, $\eta_{\rm L} < 1$. |
| − | '''(6)''' | + | '''(6)''' With the maximum value $s_{0}$ and the result of question '''(1)''': |
:$$s_{\rm eff} = \sqrt{{ E_{\rm B}}/{T}}= \sqrt{{ 2/3 \cdot s_{0}^2}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}C_{\rm S} ={ s_{\rm 0}}/{s_{\rm eff}}= \sqrt{{ 3}/{2}}\hspace{0.1cm}\underline { \approx 1.225}\hspace{0.05cm}.$$ | :$$s_{\rm eff} = \sqrt{{ E_{\rm B}}/{T}}= \sqrt{{ 2/3 \cdot s_{0}^2}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}C_{\rm S} ={ s_{\rm 0}}/{s_{\rm eff}}= \sqrt{{ 3}/{2}}\hspace{0.1cm}\underline { \approx 1.225}\hspace{0.05cm}.$$ | ||
| − | '''(7)''' | + | '''(7)''' The system efficiency under peak limitation is smaller than that under power limitation, because the non-optimal transmitted signal (too small energy) plays a role here in addition to the mismatch: |
:$$\eta_{\rm A} = \frac{1}{C_{\rm S}^2}\cdot \eta_{\rm L} = \frac{ 2}{3} \cdot 0.5625 =\hspace{0.1cm}\underline { 0.375} \hspace{0.05cm}.$$ | :$$\eta_{\rm A} = \frac{1}{C_{\rm S}^2}\cdot \eta_{\rm L} = \frac{ 2}{3} \cdot 0.5625 =\hspace{0.1cm}\underline { 0.375} \hspace{0.05cm}.$$ | ||
Revision as of 16:13, 18 March 2022
The receiver of a binary message transmission system with symbol duration $T$ consists of an integrator, which is represented by the impulse response
- $$h_{\rm E}(t) = \left\{ \begin{array}{c} 1/T \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} \hspace{0.05cm}|t| < T/2 \hspace{0.05cm}, \\ |t| > T/2 \\ \end{array}$$
This is followed by a threshold decision with optimal parameters.
The basic transmission pulse $g_{s}(t)$ according to the diagram is generally trapezoidal and is parameterized by the time $T_{1}$:
- For $T_{1} = 0$ the result is a triangular pulse, for $T_{1} = T$ the NRZ rectangle.
- The absolute pulse duration $T_{\rm S}$ is always equal to the symbol duration $T$, i.e. the distance between two transmission pulses.
The signal-to-noise power ratio (SNR) before the threshold decision can be calculated as follows, assuming no intersymbol interfering:
- $$\rho_d = {g_0^2}/{\sigma_d^2}\hspace{0.05cm}.$$
Here, $g_{0} = g_{d}(t = 0)$ is the maximum value of the basic transmitter pulse and
- $$\sigma_d^2 = {N_0}/{2} \cdot \int_{-\infty}^{+\infty}|h_{\rm E}(t)|^2 \,{\rm d} t = \frac{N_0}{2 \cdot T}$$
the noise power after the receiver filter in the presence of AWGN noise at its input.
In the course of this exercise, the following quantities will be used:
- $\rho_{d,\rm\hspace{0.05cm} max | L}$ is the maximum SNR under the constraint of power limitation.
- $\rho_{d,\rm\hspace{0.05cm} max | A}$ is the maximum SNR under peak limitation (amplitude limitation).
These definitions can be used to specify the system efficiencies:
- $$\eta_{\rm L} = \ \frac{\rho_d}{\rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm}|\hspace{0.05cm} L}}}\hspace{0.05cm},$$
- $$\eta_{\rm A} = \ \frac{\rho_d}{\rho_{d, \hspace{0.05cm}{\rm max\hspace{0.05cm} | \hspace{0.05cm} A}}} = {1}/{C_{\rm S}^2}\cdot \eta_{\rm L} \hspace{0.05cm}.$$
Here, the crest factor $C_{\rm S}$ denotes the ratio between the maximum value and the rms value (root of power) of the transmitted signal $s(t)$.
Notes:
- The exercise belongs to the chapter Optimization of Baseband Transmission Systems.
- Use the following numerical values to solve the exercise:
- $$s_0^2 = 10\,{\rm mW},\hspace{0.2cm}T = 3\,{\rm{ µ s}}, \hspace{0.2cm}N_0 = 3 \cdot 10^{-10}\,{\rm W/Hz}\hspace{0.05cm}.$$
Questions
Solution
- This gives for the transmitted pulse energy:
- $$E_{\rm B} = \int_{-\infty}^{+\infty}g_s^2(t) \,{\rm d} t = 2 \cdot \int_{0}^{T_1\hspace{0.0cm}'}g_s^2(t) \,{\rm d} t\hspace{0.2cm}+ \hspace{0.2cm}2 \cdot \int_{T_1\hspace{0.0cm}'}^{T/2}g_s^2(t) \,{\rm d} t \hspace{0.05cm}.$$
- According to this division, it can also be written:
- $${E_{\rm B}}/{2} = s_0^2 \cdot T_1\hspace{0.0cm}' + E_2 \hspace{0.05cm},\hspace{0.3cm}{\rm with}\hspace{0.3cm} E_{\rm 2} = \ \int_{T_1\hspace{0.0cm}'}^{T/2}g_s^2(t) \,{\rm d} t = s_0^2 \cdot \int_{0}^{T_2\hspace{0.0cm}'}\left ( 1 - \frac {t}{T_2\hspace{0.0cm}'}\right )^2 \,{\rm d} t $$
- $$\Rightarrow \hspace{0.3cm}E_{\rm 2} = \ s_0^2 \cdot \left [ \int_{0}^{T_2\hspace{0.0cm}'}\,\,{\rm d} t- \frac {2}{T_2\hspace{0.0cm}'} \cdot \int_{0}^{T_2\hspace{0.0cm}'}t \,\,{\rm d} t + \frac {1}{(T_2\hspace{0.0cm}'\hspace{0.02cm})^2} \cdot \int_{0}^{T_2\hspace{0.0cm}'}t^2 \,\,{\rm d} t\right ] = \ s_0^2 \cdot \left [ {T_2\hspace{0.0cm}'} - \frac {2}{T_2\hspace{0.0cm}'} \cdot \frac {(T_2\hspace{0.0cm}'\hspace{0.02cm})^2}{2} + \frac {1}{(T_2\hspace{0.0cm}'\hspace{0.02cm})^2} \cdot \frac {(T_2\hspace{0.0cm}'\hspace{0.02cm})^3}{3}\right ] = s_0^2 \cdot\frac {T_2\hspace{0.0cm}'\hspace{0.02cm}}{3} \hspace{0.05cm}.$$
- Substituted into the above equation one obtains:
- $${E_{\rm B}}/{2} = s_0^2 \cdot \frac {T_1}{2}+ s_0^2 \cdot \frac {T-T_1}{2 \cdot 3}= s_0^2 \cdot \left [\frac{T}{6} + \frac{T_1}{3}\right ]\hspace{0.3cm} \hspace{0.3cm}\Rightarrow E_{\rm B} = {s_0^2}/{3}\cdot \left (T + 2 \cdot T_1 \right )\hspace{0.05cm}.$$
- With the given values ${s_{0}}^{2} = 10 \ \rm mW$ and $T = 3\ \rm µ s$ we obtain:
- $$T_1 = 0\text{:} \hspace{0.75cm} {E_{\rm B}} = \ 1/3 \cdot{s_0^2 \cdot T}= 1/3 \cdot {10^{-2}\,{\rm W} \cdot 3 \cdot 10^{-6}\,{\rm s}} \hspace{0.1cm}\underline {= 1 \cdot 10^{-8}\,{\rm Ws}}\hspace{0.05cm},$$
- $$T_1 = T/2\text{:} \hspace{0.2cm} {E_{\rm B}} = \ 2/3 \cdot{ s_0^2 \cdot T}= \hspace{2.6cm}\text{...} \hspace{1.4cm}\hspace{0.1cm}\underline {= 2 \cdot 10^{-8}\,{\rm Ws}} \hspace{0.05cm},$$
- $$T_1 = T\text{:} \hspace{0.65cm} {E_{\rm B}} = \ { s_0^2 \cdot T}= \hspace{3.65cm}\text{...} \hspace{1.4cm}\hspace{0.1cm}\underline {= 3 \cdot 10^{-8}\,{\rm Ws}} \hspace{0.05cm}.$$
(2) The system efficiency under power limitation is maximum $(\eta_{\rm L} = 1)$, when the basic transmission pulse $g_{s}(t)$ has the same shape as the impulse response $h_{\rm E}(t)$. This is true here for the NRZ transmitted pulse: $T_1/T \ \underline{= 1}$.
(3) Under the condition given in question (2), the maximum SNR is obtained:
- $$\rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm}| \hspace{0.05cm} L}}= \frac{2 \cdot E_{\rm B}}{N_0} = \frac{2 \cdot 3 \cdot 10^{-8}\,{\rm Ws}}{3 \cdot 10^{-10}\,{\rm W/Hz}}\hspace{0.1cm}\underline {= 200} \hspace{0.05cm}.$$
(4) In general, $g_{d}(t) = g_{s}(t) ∗ h_{\rm E}(t)$. For $t = 0$, $T_1 = T/2$ gives the trapezoidal area for this:
- $$g_0 = g_d(t=0) = \frac{1}{T} \cdot \int_{-\infty}^{+\infty}g_s(t) \,{\rm d} t = \frac{T + T_1}{2} \cdot s_0 = 0.75 \cdot 0.1 \cdot \sqrt{\rm W} \hspace{0.1cm}\underline {= 0.075 \,\sqrt{\rm W}} \hspace{0.05cm}.$$
(5) With $T_1 = T/2$ (trapezoidal transmitted pulses), we obtain for the signal-to-noise ratio:
- $$\rho_d = \frac{g_0^2}{\sigma_d^2}\hspace{0.3cm}{\rm with}\hspace{0.3cm} g_0^2=0.075^2\, {\rm W},\hspace{0.1cm} \sigma_d^2 = \frac{N_0}{2 \cdot T} = 5 \cdot 10^{-5}\,{\rm W}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}\rho_d = \frac{0.075^2\, {\rm W}}{5 \cdot 10^{-5}\,{\rm W}} = 112.5 \hspace{0.05cm}.$$
- Thus, the system efficiency under power limitation with the result of (3):
- $$\eta_{\rm L} = \frac{\rho_d}{\rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm} | \hspace{0.05cm} L}}}= \frac{112.5}{200}\hspace{0.1cm}\underline {= 0.5625 }\hspace{0.05cm}.$$
- Due to the mismatch, $\eta_{\rm L} < 1$.
(6) With the maximum value $s_{0}$ and the result of question (1):
- $$s_{\rm eff} = \sqrt{{ E_{\rm B}}/{T}}= \sqrt{{ 2/3 \cdot s_{0}^2}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}C_{\rm S} ={ s_{\rm 0}}/{s_{\rm eff}}= \sqrt{{ 3}/{2}}\hspace{0.1cm}\underline { \approx 1.225}\hspace{0.05cm}.$$
(7) The system efficiency under peak limitation is smaller than that under power limitation, because the non-optimal transmitted signal (too small energy) plays a role here in addition to the mismatch:
- $$\eta_{\rm A} = \frac{1}{C_{\rm S}^2}\cdot \eta_{\rm L} = \frac{ 2}{3} \cdot 0.5625 =\hspace{0.1cm}\underline { 0.375} \hspace{0.05cm}.$$