Difference between revisions of "Aufgaben:Exercise 2.07: Reed-Solomon Code (7, 3, 5) to Base 8"
From LNTwww
| (32 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Definition_and_Properties_of_Reed-Solomon_Codes}} |
| − | [[File: | + | [[File:EN_KC_A_2_7.png|right|frame|$\rm GF(2^3)$ representation as powers, polynomials, vectors]] |
| − | + | The Reed–Solomon code considered here, denoted $\rm RSC \, (7, \, 3, \, 5)_8$, | |
| − | * | + | * encodes a block of information $\underline{u} = (u_0, \, u_1, \, u_2)$ of $k = 3$ symbols, where $u_0, \, u_1, \, u_2 ∈ \rm GF(2^3)$ applies, representing symbols rather than bits; |
| − | |||
| − | |||
| + | * generates a code word $\underline{c} = (c_0, \, c_1,\hspace{0.05cm} \text{...} \hspace{0.1cm} , c_6)$ of length $n = 7$ with code symbols $c_i$ also from the Galois field $\rm GF(2^3)$; | ||
| − | + | * has the free distance $d_{\rm min} = n - k + 1 = 5$, so that up to $e = 4$ symbol errors can be detected and up to $t = 2$ symbol errors can be corrected. | |
| + | |||
| + | |||
| + | The elements of the underlying Galois field are: | ||
:$${\rm GF}(2^3) = \{\hspace{0.1cm} 0\hspace{0.05cm},\hspace{0.1cm} 1 \hspace{0.05cm},\hspace{0.1cm} | :$${\rm GF}(2^3) = \{\hspace{0.1cm} 0\hspace{0.05cm},\hspace{0.1cm} 1 \hspace{0.05cm},\hspace{0.1cm} | ||
\alpha\hspace{0.05cm},\hspace{0.1cm} \alpha^{2} | \alpha\hspace{0.05cm},\hspace{0.1cm} \alpha^{2} | ||
| Line 17: | Line 19: | ||
\hspace{0.1cm}\}\hspace{0.05cm}. $$ | \hspace{0.1cm}\}\hspace{0.05cm}. $$ | ||
| − | + | These elements can also be represented as polynomials or as coefficient vectors according to the graphic. | |
| − | |||
| − | + | # One can see from the above table that all $u_i ∈ \rm GF(2^3)$ and all $c_i ∈ \rm GF(2^3)$ can also be characterized by $m = 3 \ \ \rm bits$, for example $\alpha^4$ by "$110$". | |
| − | * | + | # In this exercise, you are to trace the encoding process for the binary input sequence |
| − | * | + | ::$$110 \hspace{0.09cm}001\hspace{0.09cm} 011\hspace{0.09cm} 000\hspace{0.09cm} 000\hspace{0.09cm} 000\hspace{0.09cm} 111 \hspace{0.05cm} \text{...} $$ |
| − | * | + | |
| + | Note that: | ||
| + | * The Reed–Solomon coder works blockwise. In the first coding step, the code symbols $c_0, \hspace{0.05cm} \text{...} \hspace{0.1cm} , c_6$ are generated, then in the second step from the information block $\underline{u} = (u_3, \, u_4, \, u_5)$ the symbols $(c_7, \hspace{0.05cm} \text{...} \hspace{0.1cm} , c_{13})$ of the second code word, etc. | ||
| + | * One describes the information block $\underline{u}$ by the polynomial $u(x) = u_0 + u_1 \cdot x + u_2 \cdot x^2$ of degree $2$. In general, for the Galois field $\rm GF(2^m)$ the degree of the polynomial results to $m - 1$. | ||
| + | * The code symbols $c_0, \hspace{0.05cm} \text{...} \hspace{0.1cm} , c_6$ are obtained by substituting into the polynomial $u(x)$ for the parameter $x$ all elements of $\rm GF(2^3)$ except the zero element: | ||
:$${\rm GF}(2^3)\hspace{-0.01cm}\setminus \hspace{-0.01cm}\{ 0\} = \{\hspace{0.1cm}\alpha^{0}\hspace{0.05cm},\hspace{0.1cm} | :$${\rm GF}(2^3)\hspace{-0.01cm}\setminus \hspace{-0.01cm}\{ 0\} = \{\hspace{0.1cm}\alpha^{0}\hspace{0.05cm},\hspace{0.1cm} | ||
\alpha^1\hspace{0.05cm},\hspace{0.1cm} \alpha^{2} | \alpha^1\hspace{0.05cm},\hspace{0.1cm} \alpha^{2} | ||
| Line 32: | Line 37: | ||
\hspace{0.1cm}\}\hspace{0.05cm}. $$ | \hspace{0.1cm}\}\hspace{0.05cm}. $$ | ||
| − | + | *Formally, the $\rm RSC \, (7, \, 3, \, 5)_8$ can be described as follows: | |
:$$C_{\rm RS} = \Big \{ \underline {c} = \big ( u(\alpha^{0}) \hspace{0.05cm},\hspace{0.1cm} u(\alpha^{1})\hspace{0.05cm},\hspace{0.1cm}u(\alpha^{2})\hspace{0.1cm} \big ) | :$$C_{\rm RS} = \Big \{ \underline {c} = \big ( u(\alpha^{0}) \hspace{0.05cm},\hspace{0.1cm} u(\alpha^{1})\hspace{0.05cm},\hspace{0.1cm}u(\alpha^{2})\hspace{0.1cm} \big ) | ||
\hspace{0.1cm} \big | \hspace{0.2cm} u(x) = \sum_{i = 0}^{2} u_i \cdot x^{i}\hspace{0.05cm},\hspace{0.2cm} u_i \in {\rm GF}(2^3) | \hspace{0.1cm} \big | \hspace{0.2cm} u(x) = \sum_{i = 0}^{2} u_i \cdot x^{i}\hspace{0.05cm},\hspace{0.2cm} u_i \in {\rm GF}(2^3) | ||
\Big \} \hspace{0.05cm}.$$ | \Big \} \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | === | + | Hints: |
| + | * This exercise belongs to the chapter [[Channel_Coding/Definition_and_Properties_of_Reed-Solomon_Codes| "Definition and Properties of Reed–Solomon Codes"]]. | ||
| + | |||
| + | * The [[Aufgaben:Exercise_2.08:_Generator_Polynomials_for_Reed-Solomon|"Exercise 2.8"]] is structured similarly to this one, but the generator matrix $\mathbf{G}$ is then used to generate a code word $\underline{c}$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the binary information block in the first coding step? |
| + | |type="()"} | ||
| + | - $\underline{u}_{\rm bin} = (110)$, | ||
| + | + $\underline{u}_{\rm bin} = (110_|001_|011)$, | ||
| + | - $\underline{u}_{\rm bin} = (110_|001_|0)$. | ||
| + | |||
| + | {What are the information symbols in the first coding step? | ||
| + | |type="[]"} | ||
| + | + $u_0 = \alpha^4$, | ||
| + | - $u_0 = 0$, | ||
| + | - $u_1 = \alpha^6$, | ||
| + | + $u_1 = \alpha^0$, | ||
| + | + $u_2 = \alpha^3$, | ||
| + | - $u_2 = \alpha^2$. | ||
| + | |||
| + | {What is the information block as a polynomial $u(x)$? | ||
| + | |type="()"} | ||
| + | - $u(x) = \alpha^3 \cdot x + x^2 + \alpha^4 \cdot x^3$, | ||
| + | - $u(x) = \alpha^3 + x + \alpha^4 \cdot x^2$, | ||
| + | + $u(x) = \alpha^4 + x + \alpha^3 \cdot x^2$. | ||
| + | |||
| + | {What are the code symbols $c_0, \hspace{0.05cm} \text{...} \hspace{0.1cm} ,\ c_6$ for the first coding step. | ||
|type="[]"} | |type="[]"} | ||
| − | + | + | + $c_0 = \alpha^2$, |
| − | - | + | + $c_1 = \alpha^3$, |
| + | + $c_2 = \alpha^3$, | ||
| + | + $c_3 = 1$, | ||
| + | - $c_4 = \alpha^2$, | ||
| + | - $c_5 = \alpha^4$, | ||
| + | + $c_6 = 1$. | ||
| + | |||
| + | {What is the binary code word? | ||
| + | |type="()"} | ||
| + | + $\underline{c}_{\rm bin} = 100_|011_|011_|001_|110_|100_|001$, | ||
| + | - $\underline{c}_{\rm bin} = 011_|011_|001_|110_|100_|001_|100$, | ||
| + | - $\underline{c}_{\rm bin} = 100_|111_|0$. | ||
| − | { | + | {Which statements apply to the second coding step? |
| − | |type=" | + | |type="[]"} |
| − | $ | + | + It holds $u_0 = u_1 = u_2 = 0$. |
| + | - It holds $u(x) = 1$. | ||
| + | + The code word $\underline{c} ∈ \rm GF(2^3)$ consists of seven zero symbols. | ||
| + | + The binary code word $\underline{c}_{\rm bin} ∈ \rm GF(2)$ consists of $21$ zeros. | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct is the <u>proposed solution 2</u>: |
| − | '''(2)''' | + | *All information symbols here come from the Galois field $\rm GF(2^3)$. In binary notation, each symbol is represented by three bits. |
| − | '''(3)''' | + | |
| − | '''(4)''' | + | *Because of the Reed-Solomon code parameter $k = 3$, an information block consists of three information symbols: $\underline{u} = (u_0, \, u_1, \, u_2)$. |
| − | '''(5)''' | + | |
| + | *Accordingly, the binary information block $\underline{u}_{\rm bin}$ contains exactly $3 \cdot 3 = 9$ bits. | ||
| + | |||
| + | |||
| + | '''(2)''' According to the table on the information page, there is the following relationship between the coefficient vector and the exponential representation: | ||
| + | :$$(110) \hspace{0.1cm} \Rightarrow \hspace{0.2cm} u_0 = \alpha^{4}\hspace{0.05cm},\hspace{0.6cm} | ||
| + | (001) \hspace{0.1cm} \Rightarrow \hspace{0.2cm} u_1 = \alpha^{0} = 1\hspace{0.05cm},\hspace{0.6cm} | ||
| + | (011) \hspace{0.1cm} \Rightarrow \hspace{0.2cm} u_2 = \alpha^{3}\hspace{0.05cm}. $$ | ||
| + | |||
| + | *Correct are the <u>proposed solutions 1, 4, and 5</u>. | ||
| + | |||
| + | *The information block in the first coding step is $\underline{u} = (\alpha^4, \, 1, \, \alpha^3)$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' In polynomial representation, the information block $\underline{u} = (\alpha^4, \, 1, \, \alpha^3)$ results in: | ||
| + | :$$u(x) = u_0 + u_1 \cdot x + u_2 \cdot x^2 = \alpha^{4} + x + \alpha^{3}\cdot x^2 \hspace{0.05cm}. $$ | ||
| + | |||
| + | *Therefore the <u>proposed solution 3</u> is correct. | ||
| + | |||
| + | *The first proposed solution cannot be correct, since the polynomial degree can be at most $2$, if all information and code symbols originate from $\rm GF(2^3)$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' For the code symbols you get with the polynomial representation according to the specification page: | ||
| + | :$$c_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{0} = 1) = \alpha^{4} + 1 + \alpha^{3}\cdot 1^2 = | ||
| + | (110) + (001) + (011)= (100) = \alpha^{2} \hspace{0.05cm},$$ | ||
| + | :$$c_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{1}) = \alpha^{4} + \alpha + \alpha^{5}= | ||
| + | (110) + (010) + (111) = (011) = \alpha^{3} \hspace{0.05cm},$$ | ||
| + | :$$c_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{2}) = \alpha^{4} + \alpha^{2} + \alpha^{7}= | ||
| + | (110) + (100) + (001) = (011) = \alpha^{3} \hspace{0.05cm},$$ | ||
| + | :$$c_3 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{3}) = \alpha^{4} + \alpha^{3} + \alpha^{9}= | ||
| + | (110) + (011) + (100) = (001) = 1 \hspace{0.05cm},$$ | ||
| + | :$$c_4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{4}) = \alpha^{4} + \alpha^{4} + \alpha^{11} | ||
| + | = \alpha^{4} \hspace{0.05cm},$$ | ||
| + | :$$c_5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{5}) = \alpha^{4} + \alpha^{5} + \alpha^{13}= | ||
| + | (110) + (111) + (101) = (100) = \alpha^{2} \hspace{0.05cm},$$ | ||
| + | :$$c_6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{6}) = \alpha^{4} + \alpha^{6} + \alpha^{15}= | ||
| + | (\alpha^{2} + \alpha) + (\alpha^2 +1) + \alpha = 1 \hspace{0.05cm}.$$ | ||
| + | |||
| + | *So, correct are the <u>proposed solutions 1, 2, 3, 4, 7</u>. | ||
| + | |||
| + | *The solutions to 5 and 6 are exactly reversed. | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' The <u>first proposed solution</u> is correct: | ||
| + | *This results from the result of the subtask '''(4)''' and the assignment | ||
| + | :$$\alpha^2 ↔ 100, \ \alpha^3 ↔ 011, \ \alpha^3 ↔ 011, \ 1 ↔ 001, \ \alpha^4 ↔ 110, \ \alpha^2 ↔ 100, \ 1 ↔ 001. $$ | ||
| + | *The last proposed solution cannot be correct, since the binary code word must consist of $n \cdot m = 7 \cdot 3 = 21$ bits. | ||
| + | |||
| + | * Even if you have determined only the result $c_0 = \alpha^2$ in the subtask '''(4)''', you already know that the second answer cannot be correct. | ||
| + | |||
| + | |||
| + | |||
| + | '''(6)''' The <u>statements 1, 3, 4</u> are correct: | ||
| + | *The bits 10, ... , 18 of the input sequence are all $0$ and thus also the information symbols $u_0, \ u_1, \ u_2 ∈ \rm GF(2^3)$. | ||
| + | |||
| + | *Correspondingly, $u(x) = 0$, so that all code symbols $c_i = u(x = \alpha^i)$ correspond to the zero symbol $($index: $0 ≤ i ≤ 6)$. | ||
| + | |||
| + | *The binary code sequence thus consists of $n \cdot m = 21$ "zeros". | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Channel Coding: Exercises|^2.3 Reed–Solomon Codes^]] |
Latest revision as of 18:47, 7 October 2022
The Reed–Solomon code considered here, denoted $\rm RSC \, (7, \, 3, \, 5)_8$,
- encodes a block of information $\underline{u} = (u_0, \, u_1, \, u_2)$ of $k = 3$ symbols, where $u_0, \, u_1, \, u_2 ∈ \rm GF(2^3)$ applies, representing symbols rather than bits;
- generates a code word $\underline{c} = (c_0, \, c_1,\hspace{0.05cm} \text{...} \hspace{0.1cm} , c_6)$ of length $n = 7$ with code symbols $c_i$ also from the Galois field $\rm GF(2^3)$;
- has the free distance $d_{\rm min} = n - k + 1 = 5$, so that up to $e = 4$ symbol errors can be detected and up to $t = 2$ symbol errors can be corrected.
The elements of the underlying Galois field are:
- $${\rm GF}(2^3) = \{\hspace{0.1cm} 0\hspace{0.05cm},\hspace{0.1cm} 1 \hspace{0.05cm},\hspace{0.1cm} \alpha\hspace{0.05cm},\hspace{0.1cm} \alpha^{2} \hspace{0.05cm},\hspace{0.1cm} \alpha^{3} \hspace{0.05cm},\hspace{0.1cm} \alpha^{4} \hspace{0.05cm},\hspace{0.1cm} \alpha^{5} \hspace{0.05cm},\hspace{0.1cm} \alpha^{6} \hspace{0.1cm}\}\hspace{0.05cm}. $$
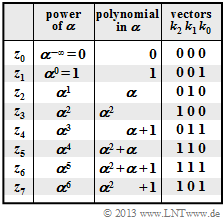
These elements can also be represented as polynomials or as coefficient vectors according to the graphic.
- One can see from the above table that all $u_i ∈ \rm GF(2^3)$ and all $c_i ∈ \rm GF(2^3)$ can also be characterized by $m = 3 \ \ \rm bits$, for example $\alpha^4$ by "$110$".
- In this exercise, you are to trace the encoding process for the binary input sequence
- $$110 \hspace{0.09cm}001\hspace{0.09cm} 011\hspace{0.09cm} 000\hspace{0.09cm} 000\hspace{0.09cm} 000\hspace{0.09cm} 111 \hspace{0.05cm} \text{...} $$
Note that:
- The Reed–Solomon coder works blockwise. In the first coding step, the code symbols $c_0, \hspace{0.05cm} \text{...} \hspace{0.1cm} , c_6$ are generated, then in the second step from the information block $\underline{u} = (u_3, \, u_4, \, u_5)$ the symbols $(c_7, \hspace{0.05cm} \text{...} \hspace{0.1cm} , c_{13})$ of the second code word, etc.
- One describes the information block $\underline{u}$ by the polynomial $u(x) = u_0 + u_1 \cdot x + u_2 \cdot x^2$ of degree $2$. In general, for the Galois field $\rm GF(2^m)$ the degree of the polynomial results to $m - 1$.
- The code symbols $c_0, \hspace{0.05cm} \text{...} \hspace{0.1cm} , c_6$ are obtained by substituting into the polynomial $u(x)$ for the parameter $x$ all elements of $\rm GF(2^3)$ except the zero element:
- $${\rm GF}(2^3)\hspace{-0.01cm}\setminus \hspace{-0.01cm}\{ 0\} = \{\hspace{0.1cm}\alpha^{0}\hspace{0.05cm},\hspace{0.1cm} \alpha^1\hspace{0.05cm},\hspace{0.1cm} \alpha^{2} \hspace{0.05cm},\hspace{0.1cm} \alpha^{3} \hspace{0.05cm},\hspace{0.1cm} \alpha^{4} \hspace{0.05cm},\hspace{0.1cm} \alpha^{5} \hspace{0.05cm},\hspace{0.1cm} \alpha^{6} \hspace{0.1cm}\}\hspace{0.05cm}. $$
- Formally, the $\rm RSC \, (7, \, 3, \, 5)_8$ can be described as follows:
- $$C_{\rm RS} = \Big \{ \underline {c} = \big ( u(\alpha^{0}) \hspace{0.05cm},\hspace{0.1cm} u(\alpha^{1})\hspace{0.05cm},\hspace{0.1cm}u(\alpha^{2})\hspace{0.1cm} \big ) \hspace{0.1cm} \big | \hspace{0.2cm} u(x) = \sum_{i = 0}^{2} u_i \cdot x^{i}\hspace{0.05cm},\hspace{0.2cm} u_i \in {\rm GF}(2^3) \Big \} \hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter "Definition and Properties of Reed–Solomon Codes".
- The "Exercise 2.8" is structured similarly to this one, but the generator matrix $\mathbf{G}$ is then used to generate a code word $\underline{c}$.
Questions
Solution
(1) Correct is the proposed solution 2:
- All information symbols here come from the Galois field $\rm GF(2^3)$. In binary notation, each symbol is represented by three bits.
- Because of the Reed-Solomon code parameter $k = 3$, an information block consists of three information symbols: $\underline{u} = (u_0, \, u_1, \, u_2)$.
- Accordingly, the binary information block $\underline{u}_{\rm bin}$ contains exactly $3 \cdot 3 = 9$ bits.
(2) According to the table on the information page, there is the following relationship between the coefficient vector and the exponential representation:
- $$(110) \hspace{0.1cm} \Rightarrow \hspace{0.2cm} u_0 = \alpha^{4}\hspace{0.05cm},\hspace{0.6cm} (001) \hspace{0.1cm} \Rightarrow \hspace{0.2cm} u_1 = \alpha^{0} = 1\hspace{0.05cm},\hspace{0.6cm} (011) \hspace{0.1cm} \Rightarrow \hspace{0.2cm} u_2 = \alpha^{3}\hspace{0.05cm}. $$
- Correct are the proposed solutions 1, 4, and 5.
- The information block in the first coding step is $\underline{u} = (\alpha^4, \, 1, \, \alpha^3)$.
(3) In polynomial representation, the information block $\underline{u} = (\alpha^4, \, 1, \, \alpha^3)$ results in:
- $$u(x) = u_0 + u_1 \cdot x + u_2 \cdot x^2 = \alpha^{4} + x + \alpha^{3}\cdot x^2 \hspace{0.05cm}. $$
- Therefore the proposed solution 3 is correct.
- The first proposed solution cannot be correct, since the polynomial degree can be at most $2$, if all information and code symbols originate from $\rm GF(2^3)$.
(4) For the code symbols you get with the polynomial representation according to the specification page:
- $$c_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{0} = 1) = \alpha^{4} + 1 + \alpha^{3}\cdot 1^2 = (110) + (001) + (011)= (100) = \alpha^{2} \hspace{0.05cm},$$
- $$c_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{1}) = \alpha^{4} + \alpha + \alpha^{5}= (110) + (010) + (111) = (011) = \alpha^{3} \hspace{0.05cm},$$
- $$c_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{2}) = \alpha^{4} + \alpha^{2} + \alpha^{7}= (110) + (100) + (001) = (011) = \alpha^{3} \hspace{0.05cm},$$
- $$c_3 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{3}) = \alpha^{4} + \alpha^{3} + \alpha^{9}= (110) + (011) + (100) = (001) = 1 \hspace{0.05cm},$$
- $$c_4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{4}) = \alpha^{4} + \alpha^{4} + \alpha^{11} = \alpha^{4} \hspace{0.05cm},$$
- $$c_5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{5}) = \alpha^{4} + \alpha^{5} + \alpha^{13}= (110) + (111) + (101) = (100) = \alpha^{2} \hspace{0.05cm},$$
- $$c_6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{6}) = \alpha^{4} + \alpha^{6} + \alpha^{15}= (\alpha^{2} + \alpha) + (\alpha^2 +1) + \alpha = 1 \hspace{0.05cm}.$$
- So, correct are the proposed solutions 1, 2, 3, 4, 7.
- The solutions to 5 and 6 are exactly reversed.
(5) The first proposed solution is correct:
- This results from the result of the subtask (4) and the assignment
- $$\alpha^2 ↔ 100, \ \alpha^3 ↔ 011, \ \alpha^3 ↔ 011, \ 1 ↔ 001, \ \alpha^4 ↔ 110, \ \alpha^2 ↔ 100, \ 1 ↔ 001. $$
- The last proposed solution cannot be correct, since the binary code word must consist of $n \cdot m = 7 \cdot 3 = 21$ bits.
- Even if you have determined only the result $c_0 = \alpha^2$ in the subtask (4), you already know that the second answer cannot be correct.
(6) The statements 1, 3, 4 are correct:
- The bits 10, ... , 18 of the input sequence are all $0$ and thus also the information symbols $u_0, \ u_1, \ u_2 ∈ \rm GF(2^3)$.
- Correspondingly, $u(x) = 0$, so that all code symbols $c_i = u(x = \alpha^i)$ correspond to the zero symbol $($index: $0 ≤ i ≤ 6)$.
- The binary code sequence thus consists of $n \cdot m = 21$ "zeros".